Hinton創(chuàng)建的向量學(xué)院的研究者提出了一類新的神經(jīng)網(wǎng)絡(luò)模型，神經(jīng)常微分方程（Neural ODE），將神經(jīng)網(wǎng)絡(luò)與常微分方程結(jié)合在一起，用ODE來做預(yù)測。不是逐層更新隱藏層，而是用神經(jīng)網(wǎng)絡(luò)來指定它們的衍生深度，用ODE求解器自適應(yīng)地計算輸出。

我們知道神經(jīng)網(wǎng)絡(luò)是一種大的分層模型，能夠從復(fù)雜的數(shù)據(jù)中學(xué)習(xí)模式。這也是為什么神經(jīng)網(wǎng)絡(luò)在處理圖像、聲音、視頻和序列行動時有很多成功的應(yīng)用。但我們常常忘記一點，那就是神經(jīng)網(wǎng)絡(luò)也是一種通用函數(shù)逼近器，因此，神經(jīng)網(wǎng)絡(luò)可以作為數(shù)值分析工具，用來解決更多的“經(jīng)典”數(shù)學(xué)問題，比如常微分方程（Ordinary Differential Equation，ODE）。

2015年橫空出世的殘差網(wǎng)絡(luò)ResNet，已經(jīng)成為深度學(xué)習(xí)業(yè)界的一個經(jīng)典模型，ResNet對每層的輸入做一個reference，學(xué)習(xí)形成殘差函數(shù)，這種殘差函數(shù)更容易優(yōu)化，使網(wǎng)絡(luò)層數(shù)大大加深。不少研究者都將 ResNet 作為近似ODE求解器，展開了對 ResNet的可逆性（reversibility）和近似計算的研究。

在一篇最新的論文里，來自多倫多大學(xué)和“深度學(xué)習(xí)教父”Geoffrey Hinton創(chuàng)建的向量學(xué)院的幾位研究者，將深度學(xué)習(xí)與ODE求解器相結(jié)合，提出了“神經(jīng)ODE”（Neural ODE），用更通用的方式展示了這些屬性。

他們將神經(jīng)ODE作為模型組件，為時間序列建模、監(jiān)督學(xué)習(xí)和密度估計開發(fā)了新的模型。這些新的模型能夠根據(jù)每個輸入來調(diào)整其評估策略，并且能顯式地控制計算速度和精度之間的權(quán)衡。

將深度學(xué)習(xí)和常微分方程結(jié)合在一起，提供四大優(yōu)勢

殘差網(wǎng)絡(luò)、遞歸神經(jīng)網(wǎng)絡(luò)解碼器和標準化流（normalizing flows）之類模型，通過將一系列變化組合成一個隱藏狀態(tài)（hidden state）來構(gòu)建復(fù)雜的變換:

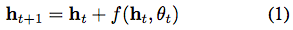
其中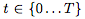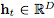，。這些迭代更新可以看作是連續(xù)變換的歐拉離散化。

當(dāng)我們向網(wǎng)絡(luò)中添加更多的層，并采取更少的步驟時會發(fā)生什么呢？在極限情況下，我們使用神經(jīng)網(wǎng)絡(luò)指定的常微分方程（ODE）來參數(shù)化隱藏單元的連續(xù)動態(tài)：

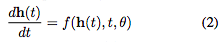
從輸入層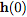開始，我們可以將輸出層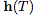定義為在某個時間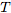時這個ODE的初始值問題的解。這個值可以通過黑盒微分方程求解器來計算，該求解器在必要的時候評估隱藏單元動態(tài)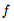，以確定所需精度的解。圖1對比了這兩種方法。

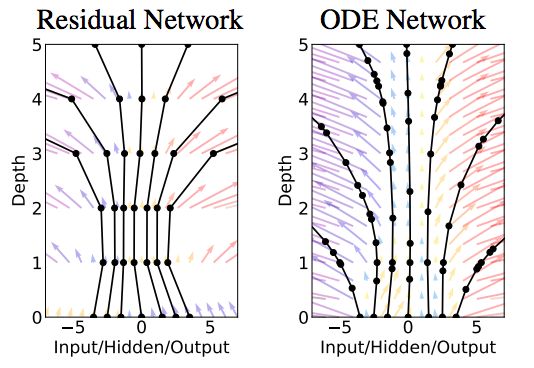
圖1：左：殘差網(wǎng)絡(luò)定義一個離散的有限變換序列。右：ODE網(wǎng)絡(luò)定義了一個向量場，它不斷地變換狀態(tài)。圓圈代表評估位置。

使用ODE求解器定義和評估模型有以下幾個好處：

內(nèi)存效率。在論文第2章，我們解釋了如何計算任何ODE求解器的所有輸入的標量值損失的梯度，而不通過求解器的操作進行反向傳播。不存儲任何中間量的前向通道允許我們以幾乎不變的內(nèi)存成本來訓(xùn)練模型，這是訓(xùn)練深度模型的一個主要瓶頸。

自適應(yīng)計算。歐拉方法（Euler’s method）可能是求解ODE最簡單的方法。現(xiàn)代的ODE求解器提供了有關(guān)近似誤差增長的保證，檢測誤差的大小并實時調(diào)整其評估策略，以達到所要求的精度水平。這使得評估模型的成本隨著問題復(fù)雜度而增加。訓(xùn)練結(jié)束后，可以降低實時應(yīng)用或低功耗應(yīng)用的精度。

參數(shù)效率。當(dāng)隱藏單元動態(tài)（hidden unit dynamics）被參數(shù)化為時間的連續(xù)函數(shù)時，附近“l(fā)ayers”的參數(shù)自動連接在一起。在第3節(jié)中，我們表明這減少了監(jiān)督學(xué)習(xí)任務(wù)所需的參數(shù)數(shù)量。

可擴展的和可逆的normalizing flows。連續(xù)變換的一個意想不到的好處是變量公式的變化更容易計算了。在第4節(jié)中，我們推導(dǎo)出這個結(jié)果，并用它構(gòu)造了一類新的可逆密度模型，該模型避免了normalizing flows的單個單元瓶頸，并且可以通過最大似然法直接進行訓(xùn)練。

連續(xù)時間序列模型。與需要離散觀測和發(fā)射間隔的遞歸神經(jīng)網(wǎng)絡(luò)不同，連續(xù)定義的動態(tài)可以自然地并入任意時間到達的數(shù)據(jù)。在第5節(jié)中，我們構(gòu)建并演示了這樣一個模型。

ODE求解器提供了一個通用的反向傳播算法

論文作者、多倫多大學(xué)助理教授David Duvenaud表示，他們通過ODE求解器，提供了一個通用的backprop，但他們的方法是從可逆性上入手，而不是在ODE求解器的運算里進行反向傳播（因為這樣做對內(nèi)存消耗很大）。這個方法已經(jīng)添加到 autograd。

另一位作者、多倫多大學(xué)的博士生Tian Qi Chen也表示，他們這項工作創(chuàng)新的地方就在于提出并且開源了一種新方法，在自動微分的框架下，將ODE和深度學(xué)習(xí)結(jié)合在一起。

此外，這項研究還得到了很多意外的收獲。例如，構(gòu)建了連續(xù)標準化流（continuous normalizing flows），可逆性強，可以使用寬度，就像 Real NVP一樣，但不需要對數(shù)據(jù)維度分區(qū)或排序。

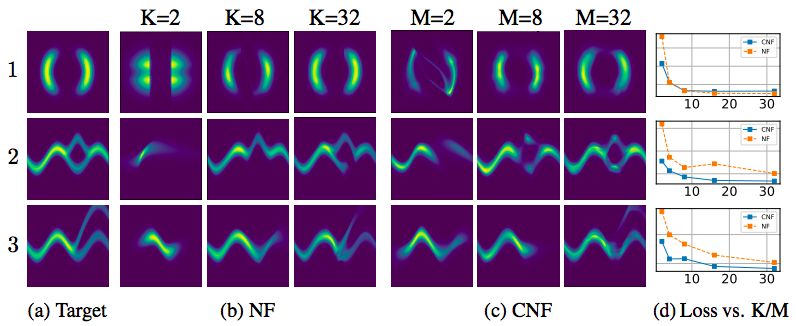
標準化流與連續(xù)標準化流量的比較。標準化流的模型容量由網(wǎng)絡(luò)的深度（K）決定，而連續(xù)標準化流的模型容量可以通過增加寬度（M）來增加，使它們更容易訓(xùn)練。來源：研究論文

還有時間連續(xù)RNN（continuous-time RNNs），能夠處理不規(guī)則的觀察時間，同時用狀態(tài)依賴的泊松過程近似建模。下圖展示了普通的RNN和神經(jīng)ODE對比：

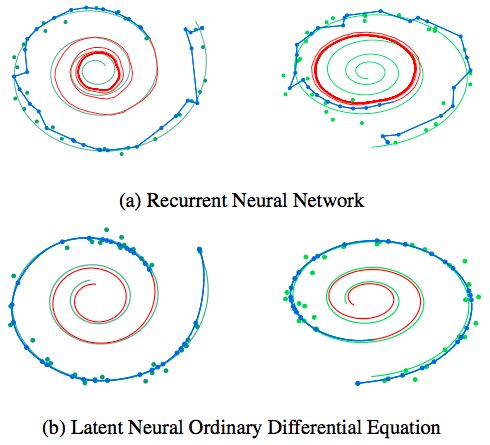
Tian Qi Chen說，他尤其喜歡變量的即時改變，這打開了一種新的方法，用連續(xù)標準流進行生成建模。

目前，作者正在講ODE求解器拓展到GPU上，做更大規(guī)模的擴展。