MIT CSAIL的研究人員發(fā)現(xiàn)，隱藏層僅有一個(gè)神經(jīng)元的ResNet就是一個(gè)通用的函數(shù)逼近器，恒等映射確實(shí)加強(qiáng)了深度網(wǎng)絡(luò)的表達(dá)能力。研究人員表示，這一發(fā)現(xiàn)還填補(bǔ)了全連接網(wǎng)絡(luò)表達(dá)能力強(qiáng)大原因的理論空白。

深度神經(jīng)網(wǎng)絡(luò)是當(dāng)前很多機(jī)器學(xué)習(xí)應(yīng)用成功的關(guān)鍵，而深度學(xué)習(xí)的一大趨勢(shì)，就是神經(jīng)網(wǎng)絡(luò)越來(lái)越深：以計(jì)算機(jī)視覺(jué)應(yīng)用為例，從最開(kāi)始的AlexNet，到后來(lái)的VGG-Net，再到最近的ResNet，網(wǎng)絡(luò)的性能確實(shí)隨著層數(shù)的增多而提升。

研究人員的一個(gè)直觀感受是，隨著網(wǎng)絡(luò)深度的增大，網(wǎng)絡(luò)的容量也變高，更容易去逼近某個(gè)函數(shù)。

因此，從理論方面，也有越來(lái)越多的人開(kāi)始關(guān)心，是不是所有的函數(shù)都能夠用一個(gè)足夠大的神經(jīng)網(wǎng)絡(luò)去逼近？

在一篇最新上傳Arxiv的論文里，MIT CSAIL的兩位研究人員從ResNet結(jié)構(gòu)入手，論證了這個(gè)問(wèn)題。他們發(fā)現(xiàn)，在每個(gè)隱藏層中只有一個(gè)神經(jīng)元的ResNet，就是一個(gè)通用逼近函數(shù)，無(wú)論整個(gè)網(wǎng)絡(luò)的深度有多少，哪怕趨于無(wú)窮大，這一點(diǎn)都成立。

一個(gè)神經(jīng)元就夠了，這不是很令人興奮嗎？

從深度上理解通用逼近定理

關(guān)于神經(jīng)網(wǎng)絡(luò)的表達(dá)能力（representational power）此前已經(jīng)有很多討論。

上世紀(jì)80年代的一些研究發(fā)現(xiàn)，只要有足夠多的隱藏層神經(jīng)元，擁有單個(gè)隱藏層的神經(jīng)網(wǎng)絡(luò)能以任意精度逼近任意連續(xù)函數(shù)。這也被稱為通用逼近定理（universal approximation theorem）。

但是，這是從“寬度”而非“深度”的角度去理解——不斷增加隱藏層神經(jīng)元，增加的是網(wǎng)絡(luò)的寬度——而實(shí)際經(jīng)驗(yàn)告訴我們，深度網(wǎng)絡(luò)才是最適用于去學(xué)習(xí)能解決現(xiàn)實(shí)世界問(wèn)題的函數(shù)的。

因此，這就自然引出了一個(gè)問(wèn)題：

如果每層的神經(jīng)元數(shù)量固定，當(dāng)網(wǎng)絡(luò)深度增加到無(wú)窮大的時(shí)候，通用逼近定理還成立嗎？

北京大學(xué)Zhou Lu等人發(fā)表在NIPS 2017的文章《The Expressive Power of Neural Networks: A View from the Width》發(fā)現(xiàn)，對(duì)于用ReLU作為激活函數(shù)的全連接神經(jīng)網(wǎng)絡(luò)，當(dāng)每個(gè)隱藏層至少有 d+4 個(gè)神經(jīng)元（d表示輸入空間）時(shí)，通用逼近定理就成立，但至多有 d 個(gè)神經(jīng)元時(shí)，就不成立。

那么，換一種結(jié)構(gòu)，這個(gè)條件還會(huì)成立嗎？究竟是什么在影響深度網(wǎng)絡(luò)的表達(dá)能力？

MIT CSAIL的這兩位研究人員便想到了ResNet。

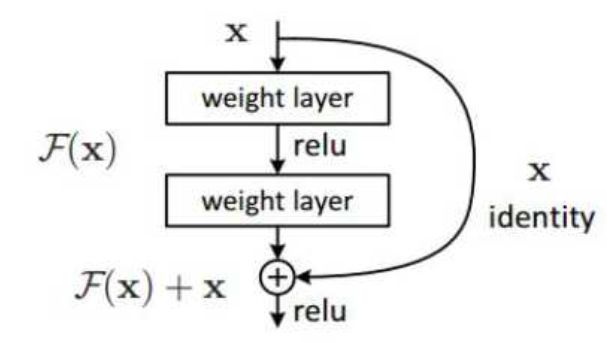
從何愷明等人2015年提出以來(lái)，ResNet甚至被認(rèn)為是當(dāng)前性能最佳的網(wǎng)絡(luò)結(jié)構(gòu)。ResNet的成功得益于它引入了快捷連接（shortcut connection），以及在此基礎(chǔ)上的恒等映射（Identity Mapping），使數(shù)據(jù)流可以跨層流動(dòng)。原問(wèn)題就轉(zhuǎn)化使殘差函數(shù)（F(x)=H(x)-x）逼近0值，而不用直接去擬合一個(gè)恒等函數(shù) H’(x)。

由于恒等映射，ResNet的寬度與輸入空間相等。因此，作者構(gòu)建了這樣的結(jié)構(gòu)，并不斷縮小隱藏層，看看極限在哪里：

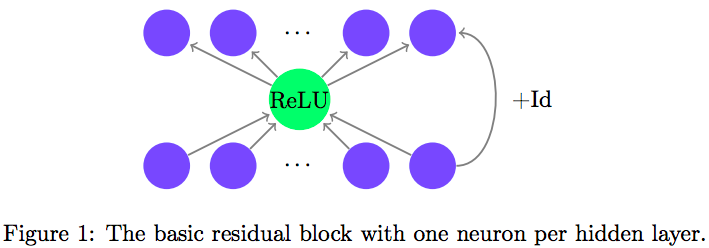
結(jié)果就如上文所說(shuō)的那樣，最少只需要一個(gè)神經(jīng)元就夠了。

作者表示，這進(jìn)一步從理論上表明，ResNet的恒等映射確實(shí)增強(qiáng)了深度網(wǎng)絡(luò)的表達(dá)能力。

例證：完全連接網(wǎng)絡(luò)和ResNet之間的區(qū)別

作者給出了一個(gè)這樣的toy example：我們首先通過(guò)一個(gè)簡(jiǎn)單的例子，通過(guò)實(shí)證探索一個(gè)完全連接網(wǎng)絡(luò)和ResNet之間的區(qū)別，其中完全連接網(wǎng)絡(luò)的每個(gè)隱藏層有 d 個(gè)神經(jīng)元。例子是：在平面中對(duì)單位球（unit ball）進(jìn)行分類。

訓(xùn)練集由隨機(jī)生成的樣本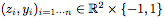組成，其中?

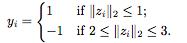
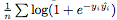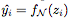我們?nèi)藶榈卦谡龢颖竞拓?fù)樣本之間創(chuàng)建了一個(gè)邊界，以使分類任務(wù)更容易。我們用邏輯損失作為損失，其中是網(wǎng)絡(luò)在第 i 個(gè)樣本的輸出。在訓(xùn)練結(jié)束后，我們描繪了各種深度的網(wǎng)絡(luò)學(xué)習(xí)的決策邊界。理想情況下，我們希望模型的決策邊界接近真實(shí)分布。

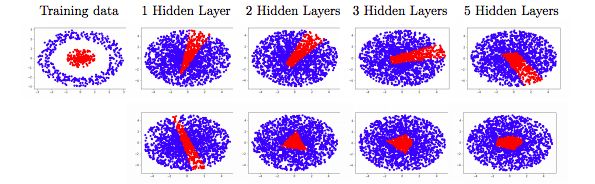
圖2：在單位球分類問(wèn)題中，訓(xùn)練每個(gè)隱藏層（上面一行）寬度 d = 2 的全連接網(wǎng)絡(luò)和每個(gè)隱藏層只有一個(gè)神經(jīng)元的 ResNet（下面一行）得到的決策邊界。全連接網(wǎng)絡(luò)無(wú)法捕獲真正的函數(shù)，這與認(rèn)為寬度 d 對(duì)于通用逼近而言太窄（narrow）的理論是一致的。相反，ResNet很好地逼近了函數(shù)，支持了我們的理論結(jié)果。

圖2顯示了結(jié)果。對(duì)于完全連接網(wǎng)絡(luò)（上面一行）而言，學(xué)習(xí)的決策邊界對(duì)不同的深度具有大致相同的形狀：逼近質(zhì)量似乎沒(méi)有隨著深度增加而提高。雖然人們可能傾向于認(rèn)為這是由局部最優(yōu)性引起的，但我們的結(jié)果與文獻(xiàn)[19]中的結(jié)果一致：

Proposition 2.1. 令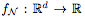為由一個(gè)具有ReLU激活的完全連接網(wǎng)絡(luò) N 定義的函數(shù)。用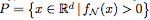表示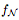的正水平集。如果 N 的每個(gè)隱藏層至多有 d 個(gè)神經(jīng)元，那么

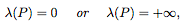, 其中 λ 表示 Lebesgue measure

換句話說(shuō)，“narrow”的完全連接網(wǎng)絡(luò)的水平集（level set）是無(wú)界的，或具有零測(cè)度。

因此，即使當(dāng)深度趨于無(wú)窮大時(shí)，“narrow”的完全連接網(wǎng)絡(luò)也不能逼近有界區(qū)域。這里我們只展示了 d=2 的情況，因?yàn)榭梢院苋菀椎乜吹綌?shù)據(jù)；在更高的維度也可以看到同樣的觀察結(jié)果。

ResNet的決策邊界看起來(lái)明顯不同：盡管寬度更窄，但ResNet表示了一個(gè)有界區(qū)域的指標(biāo)。隨著深度的增加，決策邊界似乎趨于單位球，這意味著命題2.1不能適用于ResNet。這些觀察激發(fā)了通用逼近定理。

討論

在本文中，我們展示了每個(gè)隱藏層只有一個(gè)神經(jīng)元的ResNet結(jié)構(gòu)的通用逼近定理。這個(gè)結(jié)果與最近在全連接網(wǎng)絡(luò)上的結(jié)果形成對(duì)比，對(duì)于這些全連接網(wǎng)絡(luò)，在寬度為 d 或更小時(shí)，通用逼近會(huì)失敗。

ResNet vs 全連接網(wǎng)絡(luò)：

雖然我們?cè)诿總€(gè)基本殘差塊（residual block）中只使用一個(gè)隱藏神經(jīng)元來(lái)實(shí)現(xiàn)通用逼近，但有人可能會(huì)說(shuō)，ResNet的結(jié)構(gòu)仍然將identity傳遞到下一層。這個(gè)identity map可以算作 d 個(gè)隱藏單元，導(dǎo)致每個(gè)殘差塊共有 d+1 個(gè)隱藏單元，并且使得網(wǎng)絡(luò)被看做一個(gè)寬度為 (d + 1)的完全連接網(wǎng)絡(luò)。但是，即使從這個(gè)角度看，ResNet也相當(dāng)于一個(gè)完全連接網(wǎng)絡(luò)的壓縮或稀疏版本。特別是，寬度為 (d + 1)的完全連接網(wǎng)絡(luò)每層具有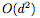個(gè)連接，而ResNet中只有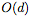個(gè)連接，這要?dú)w功于identity map。完全連接網(wǎng)絡(luò)的這種“過(guò)度參數(shù)化”或許可以解釋為什么dropout對(duì)這類網(wǎng)絡(luò)有用。

同樣的道理，我們的結(jié)果表明寬度(d + 1)的完全連接網(wǎng)絡(luò)是通用逼近器，這是新的發(fā)現(xiàn)。文獻(xiàn)[19]中的結(jié)構(gòu)要求每層d + 4個(gè)單元，在上下邊界之間留有空隙。因此，我們的結(jié)果縮小了差距：寬度為(d + 1)的完全連接網(wǎng)絡(luò)是通用逼近器，而寬度為d的完全連接網(wǎng)絡(luò)不是。

為什么通用逼近很重要？如我們?cè)谡撐牡?節(jié)所述，寬度為d的完全連接網(wǎng)絡(luò)永遠(yuǎn)不可能逼近一個(gè)緊湊的決策邊界，即使我們?cè)试S有無(wú)限的深度。然而，在高維空間中，很難對(duì)得到的決策邊界進(jìn)行可視化和檢查。通用逼近定理提供了一種完整性檢查，并確保原則上我們能夠捕獲任何期望的決策邊界。

訓(xùn)練效率：

通用逼近定理只保證了逼近任何期望函數(shù)的可能性，但它并不能保證我們通過(guò)運(yùn)行SGD或任何其他優(yōu)化算法能夠?qū)嶋H找到它。理解訓(xùn)練效率可能需要更好地理解優(yōu)化場(chǎng)景，這是最近受到關(guān)注的一個(gè)話題。

這里，我們?cè)噲D提出一個(gè)稍微不同的角度。根據(jù)我們的理論，帶有單個(gè)神經(jīng)元隱藏層（one-neuron hidden layers）的ResNet已經(jīng)是一個(gè)通用的逼近器。換句話說(shuō)，每一層有多個(gè)單元的ResNet在某種意義上是模型的過(guò)度參數(shù)化，而過(guò)度參數(shù)化已經(jīng)被觀察到有利于優(yōu)化。這可能就是為什么訓(xùn)練一個(gè)非常深的ResNet比訓(xùn)練一個(gè)完全連接的網(wǎng)絡(luò)“更容易”的原因之一。未來(lái)的工作可以更嚴(yán)謹(jǐn)?shù)胤治鲞@一點(diǎn)。

泛化：

由于一個(gè)通用逼近器可以擬合任何函數(shù)，人們可能會(huì)認(rèn)為它很容易過(guò)度擬合。然而，通常可以觀察到，深度網(wǎng)絡(luò)在測(cè)試集上的泛化效果非常出色。對(duì)這一現(xiàn)象的解釋與我們的論文是不相關(guān)的，但是，了解通用逼近能力是這一理論的重要組成部分。此外，我們的結(jié)果暗示了，前述的“過(guò)度參數(shù)化”也可能發(fā)揮作用。

總結(jié)：

總結(jié)而言，我們給出了具有單個(gè)神經(jīng)元隱藏層的ResNet的通用逼近定理。這從理論上將ResNet和完全連接網(wǎng)絡(luò)區(qū)分開(kāi)來(lái)，并且，我們的結(jié)果填補(bǔ)了理解完全連接網(wǎng)絡(luò)的表示能力方面的空白。在一定程度上，我們的結(jié)果在理論上激勵(lì)了對(duì)ResNet架構(gòu)進(jìn)行更深入的實(shí)踐。