在這篇文章中，我將回顧一個經驗法則，該法則可用于估算RMS周期間抖動，前提是你知道RMS周期抖動。我首先在實驗室中觀察了這個經驗法則，并隨后了解了更多。

該經驗法則是什么？

該法則很簡單。如果周期抖動分布是高斯或正態分布，則周期間抖動可以根據周期抖動估算如下：

Jcc (RMS)= sqrt(3) * Jper (RMS)

我首先在定時知識庫文章中記錄了這一點，該文章是EstimatingRMS Cycle to Cycle Jitter from RMS Period Jitter (https://www.silabs.com/community/timing/knowledge-base.entry.html/2011/04/11/estimating_rms_cycle-Ab6s)。我今天會花更多時間在這個想法上，并從幾個不同的角度來解決這個問題。

問題是什么？

在我們的應用筆記“A Primer On Jitter, Jitter Measurement and Phase-Locked Loops” (https://www.silabs.com/documents/public/application-notes/AN687.pdf)中，下圖顯示了后處理相位噪聲進入定時抖動指標的下列斜率。周期抖動和周期間抖動分別顯示為20dBc / dec和40dB / dec斜率的高通濾波器。要記住這樣一個有用的例子。

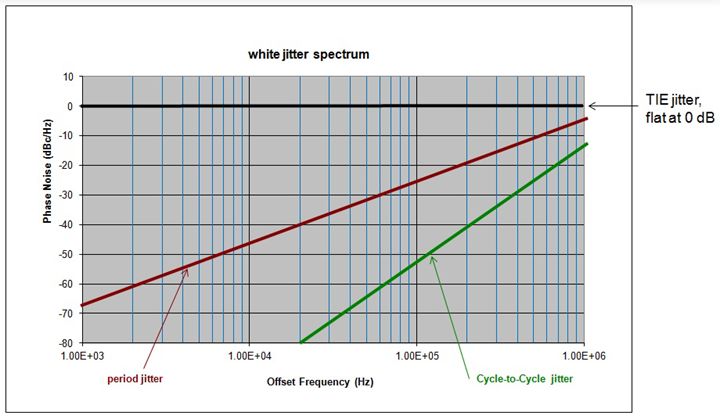
問題是，根據sqrt（3）規則，RMS周期間抖動如何大于RMS周期抖動，并且周期間抖動濾波器的斜率更陡？答案是，決定最終結果的不只是斜率。

重要術語

在繼續之前，這里有幾個來自AN279:Estimating Period Jitter from Phase Noise（https://www.silabs.com/documents/public/application-notes/AN279.pdf）的定義。

• 周期間抖動 - 相鄰時鐘周期之間的時鐘周期中的短期變化。這種抖動測量（在此縮寫為JCC）可以被特指為RMS或峰間量。

• 周期抖動 - 與平均時鐘周期相比，所有測量時鐘周期內時鐘周期的短時變化。這種抖動測量（在此縮寫為JPER）可以指定為RMS或峰間量。

實驗室測量例子

首先，下面的示例實驗測量直接來自知識庫文章。為了方便起見，帶注釋的圖像變得更加緊湊。

屏幕截圖中有三個項目被調出。

1. 在100萬次循環后的周期分布呈現高斯分布，并且非常接近于分別符合±1，±2和±3標準差的68-95-99.7％規則。

2. 測量的RMS周期抖動是周期抖動分布的標準偏差或約1.17 ps。因此，我們可以估算RMS周期以抖動為sqrt（3）* 1.17 ps或2.03 ps。

3. 實際測量的周期到周期抖動為2.05 ps，這與估算值相當接近。

Excel演示示例

您也可以在Excel模擬中演示此規則。為了探索效果，我生成了一個電子表格，其中我選取了一個理想的時鐘邊緣，然后通過從高斯分布中采集隨機樣本來抖動邊緣。然后，我進行了周期測量和周期間測量，每個周期測量30個邊沿，每個邊沿100個，時鐘邊沿表示100MHz時鐘抖動。請注意，由于周期間抖動結果是帶符號的，即正或負，所以我們應該預期這些量的標準偏差會更大，其他都相等。100個邊緣試驗通常比30個邊緣試驗更接近sqrt（3）規則，但即使在30個邊緣上仍然可以看到總體效果。

經驗法則的解釋

那么這個經驗法則是如何產生的呢？如前所述，我多年前在實驗室首次觀察到這一點。然而，我幾乎沒有看到這方面的文字。最終我找到了StatekTechnical Note 35，An overview of oscillator jitter（http://www.statek.com/products/pdf/TN-35%20Rev%20B.pdf）。下面的解釋是這個推導的一個稍微簡化和修改的版本，其中數量是“大”時間序列的期望值（回想我對100條邊優于30條邊收斂的規則）。

讓下面的變量代表單個邊緣的時間抖動的方差，即抖動邊緣與理想邊緣的時間差異。

每個測量周期是2個連續邊緣值之間的差值，其中每個邊緣抖動具有方差s2j。周期抖動有時被稱為定時抖動的第一個差異。由于周期間抖動是相鄰周期之間的差異，所以它可以被稱為定時抖動的第二差異。

如果每個邊緣的抖動是獨立的，那么周期抖動的方差可以寫為：

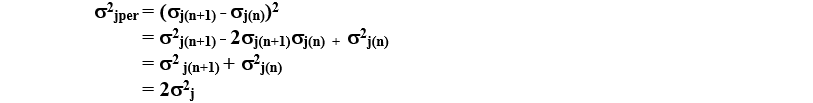
這正是我們所期望的每個“差異總和法”。你可以在這里看到一個例子，它指出了對于獨立的（不相關的）變量：

然而，我們不能很容易地計算周期循環抖動，因為在每個周期到周期的測量中，我們使用兩次“內部”時鐘沿，因此我們必須考慮到這一點。相反，我們寫道：

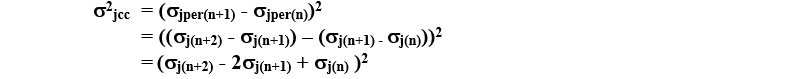
由于每個邊緣的抖動被假定為獨立的并且具有相同的統計特性，所以我們可以放棄互相關項并寫出：

因此，差異的比例

這是一個有趣而意想不到的結果，至少對我來說:)

后處理階段噪聲

AN279:Estimating Period Jitter from Phase Noise（https://www.silabs.com/documents/public/application-notes/AN279.pdf），描述了如何根據對相位噪聲積分應用4[sin（pi* f * tau）] ^ 2權重因子，從相位噪聲中估計周期抖動。加權因子主要是+20dB / dec高通濾波器，直到在半載波頻率達到峰值。

事實證明，您可以使用類似的方法計算周期間抖動。這需要應用主要是+40dB / dec高通濾波器的{4 [sin（pi * f * tau）] ^ 2} ^ 2或16 [sin（pi * f * tau）] ^ 4加權因子，直到在半載頻處達到峰值。這正是AN687所指的。

那么如何整合一個更清晰的HPF裙，使得周期間抖動大于周期抖動和sqrt（3）規則？

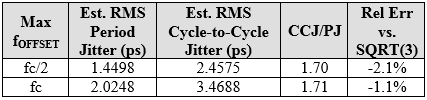
我不得不挖掘我在編寫該應用筆記時使用的舊Matlab程序。幸運的是，我仍然擁有該文件和原始數據。然后我運行該程序的修改版本，并比較maxfOFFSET的結果，其中相位噪聲數據集在fc / 2和fc處被擴展和截斷。答案是，雖然周期到周期的HPF裙子更陡峭，但最大值也更高。看下面的情節。藍色寬軌跡是周期抖動加權（濾波）相位噪聲，紅色寬軌跡是周期間抖動加權相位噪聲。這是造成差異的更大的遠偏移相位噪聲貢獻。

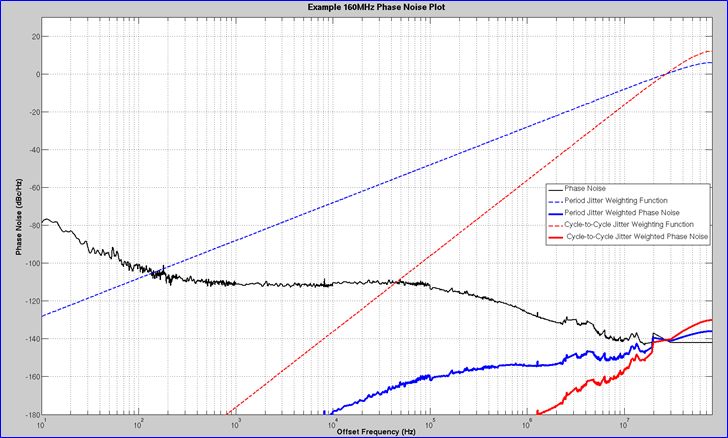
原始數據用于160 MHzCMOS振蕩器，其在約2ps時具有示波器測量周期抖動。為了保守，正是出于這個原因，我經常比fc/ 2更進一步地進行整合。現在，示波器的噪聲更低，找到待測試的原始設備并在更好的儀器上進行測量會很有趣。我的主要興趣在于看sqrt（3）關系是否成立。正如你所看到的，兩種情況下都遵循經驗法則。

結論

我希望你喜歡這篇Timing 101文章。循環周期抖動的sqrt（3）經驗法則在實驗室，Excel電子表格模擬以及后處理相位噪聲時都表現良好。