背后機制
這個章節從線性 SVM 分類器開始,將解釋 SVM 是如何做預測的并且算法是如何工作的。如果你是剛接觸機器學習,你可以跳過這個章節,直接進入本章末尾的練習。等到你想深入了解 SVM,再回頭研究這部分內容。
首先,關于符號的約定:在第 4 章,我們將所有模型參數放在一個矢量θ里,包括偏置項θ0,θ1到θn的輸入特征權重,和增加一個偏差輸入x0 = 1到所有樣本。在本章中,我們將使用一個不同的符號約定,在處理 SVM 上,這更方便,也更常見:偏置項被命名為b,特征權重向量被稱為w,在輸入特征向量中不再添加偏置特征。
決策函數和預測
線性 SVM 分類器通過簡單地計算決策函數
來預測新樣本的類別:如果結果是正的,預測類別?是正類,為 1,否則他就是負類,為 0。見公式 5-2
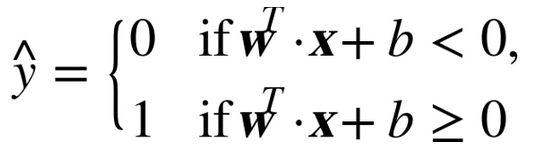
圖 5-12 顯示了和圖 5-4 右邊圖模型相對應的決策函數:因為這個數據集有兩個特征(花瓣的寬度和花瓣的長度),所以是個二維的平面。決策邊界是決策函數等于 0 的點的集合,圖中兩個平面的交叉處,即一條直線(圖中的實線)
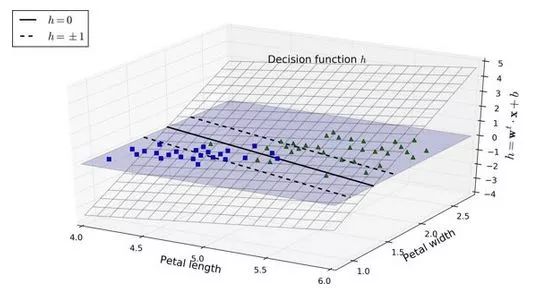
虛線表示的是那些決策函數等于 1 或 -1 的點:它們平行,且到決策邊界的距離相等,形成一個間隔。訓練線性 SVM 分類器意味著找到w值和b值使得這一個間隔盡可能大,同時避免間隔違規(硬間隔)或限制它們(軟間隔)
訓練目標
看下決策函數的斜率:它等于權重向量的范數。如果我們把這個斜率除于 2,決策函數等于 ±1 的點將會離決策邊界原來的兩倍大。換句話,即斜率除于 2,那么間隔將增加兩倍。在圖 5-13 中,2D 形式比較容易可視化。權重向量w越小,間隔越大。
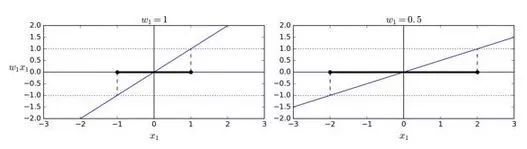
所以我們的目標是最小化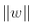 ,從而獲得大的間隔。然而,如果我們想要避免間隔違規(硬間隔),對于正的訓練樣本,我們需要決策函數大于 1,對于負訓練樣本,小于 -1。若我們對負樣本(即
,從而獲得大的間隔。然而,如果我們想要避免間隔違規(硬間隔),對于正的訓練樣本,我們需要決策函數大于 1,對于負訓練樣本,小于 -1。若我們對負樣本(即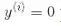 )定義
)定義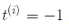 ,對正樣本(即
,對正樣本(即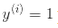 )定義
)定義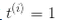 ,那么我們可以對所有的樣本表示為
,那么我們可以對所有的樣本表示為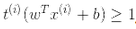
因此,我們可以將硬間隔線性 SVM 分類器表示為公式 5-3 中的約束優化問題
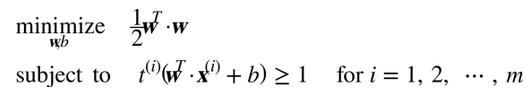
注

為了獲得軟間隔的目標,我們需要對每個樣本應用一個松弛變量(slack variable)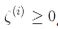
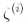 表示了第i個樣本允許違規間隔的程度。我們現在有兩個不一致的目標:一個是使松弛變量盡可能的小,從而減小間隔違規,另一個是使1/2 w·w盡量小,從而增大間隔。這時C超參數發揮作用:它允許我們在兩個目標之間權衡。我們得到了公式 5-4 的約束優化問題。
表示了第i個樣本允許違規間隔的程度。我們現在有兩個不一致的目標:一個是使松弛變量盡可能的小,從而減小間隔違規,另一個是使1/2 w·w盡量小,從而增大間隔。這時C超參數發揮作用:它允許我們在兩個目標之間權衡。我們得到了公式 5-4 的約束優化問題。
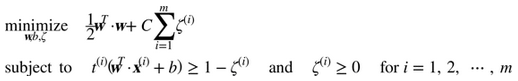
二次規劃
硬間隔和軟間隔都是線性約束的凸二次規劃優化問題。這些問題被稱之為二次規劃(QP)問題。現在有許多解決方案可以使用各種技術來處理 QP 問題,但這超出了本書的范圍。一般問題的公式在公式 5-5 給出。

對偶問題
給出一個約束優化問題,即原始問題(primal problem),它可能表示不同但是和另一個問題緊密相連,稱為對偶問題(Dual Problem)。對偶問題的解通常是對原始問題的解給出一個下界約束,但在某些條件下,它們可以獲得相同解。幸運的是,SVM 問題恰好滿足這些條件,所以你可以選擇解決原始問題或者對偶問題,兩者將會有相同解。公式 5-6 表示了線性 SVM 的對偶形式(如果你對怎么從原始問題獲得對偶問題感興趣,可以看下附錄 C)
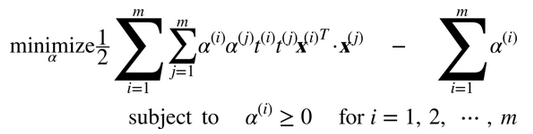
一旦你找到最小化公式的向量α(使用 QP 解決方案),你可以通過使用公式 5-7 的方法計算w和b,從而使原始問題最小化。
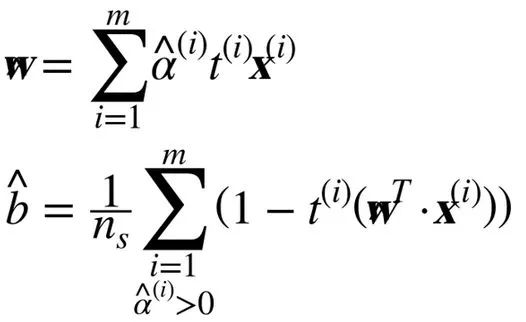
當訓練樣本的數量比特征數量小的時候,對偶問題比原始問題要快得多。更重要的是,它讓核技巧成為可能,而原始問題則不然。那么這個核技巧是怎么樣的呢?
核化支持向量機
假設你想把一個 2 次多項式變換應用到二維空間的訓練集(例如衛星數據集),然后在變換后的訓練集上訓練一個線性SVM分類器。公式 5-8 顯示了你想應用的 2 次多項式映射函數?。
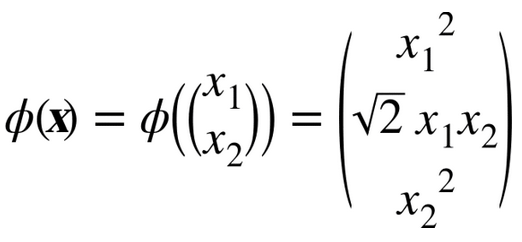
注意到轉換后的向量是 3 維的而不是 2 維。如果我們應用這個 2 次多項式映射,然后計算轉換后向量的點積(見公式 5-9),讓我們看下兩個 2 維向量a和b會發生什么。
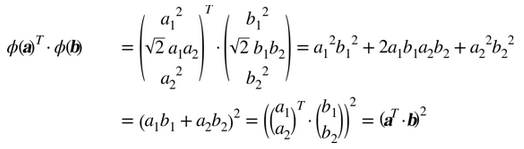
轉換后向量的點積等于原始向量點積的平方: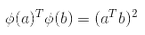

Mercer 定理
根據 Mercer 定理,如果函數K(a, b)滿足一些 Mercer 條件的數學條件(K函數在參數內必須是連續,對稱,即K(a, b)=K(b, a),等),那么存在函數?,將a和b映射到另一個空間(可能有更高的維度),有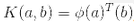 。所以你可以用K作為核函數,即使你不知道?是什么。使用高斯核(Gaussian RBF kernel)情況下,它實際是將每個訓練樣本映射到無限維空間,所以你不需要知道是怎么執行映射的也是一件好事。
。所以你可以用K作為核函數,即使你不知道?是什么。使用高斯核(Gaussian RBF kernel)情況下,它實際是將每個訓練樣本映射到無限維空間,所以你不需要知道是怎么執行映射的也是一件好事。
注意一些常用核函數(例如 Sigmoid 核函數)并不滿足所有的 Mercer 條件,然而在實踐中通常表現得很好。
我們還有一個問題要解決。公式 5-7 展示了線性 SVM 分類器如何從對偶解到原始解,如果你應用了核技巧那么得到的公式會包含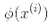 。事實上,w必須和
。事實上,w必須和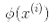 有同樣的維度,可能是巨大的維度或者無限的維度,所以你很難計算它。但怎么在不知道w的情況下做出預測?好消息是你可以將公式 5-7 的w代入到新的樣本
有同樣的維度,可能是巨大的維度或者無限的維度,所以你很難計算它。但怎么在不知道w的情況下做出預測?好消息是你可以將公式 5-7 的w代入到新的樣本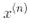 的決策函數中,你會得到一個在輸入向量之間只有點積的方程式。這時,核技巧將派上用場,見公式 5-11
的決策函數中,你會得到一個在輸入向量之間只有點積的方程式。這時,核技巧將派上用場,見公式 5-11
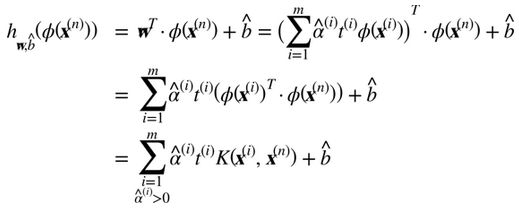
注意到支持向量才滿足α(i)≠0,做出預測只涉及計算為支持向量部分的輸入樣本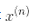 的點積,而不是全部的訓練樣本。當然,你同樣也需要使用同樣的技巧來計算偏置項b,見公式 5-12
的點積,而不是全部的訓練樣本。當然,你同樣也需要使用同樣的技巧來計算偏置項b,見公式 5-12
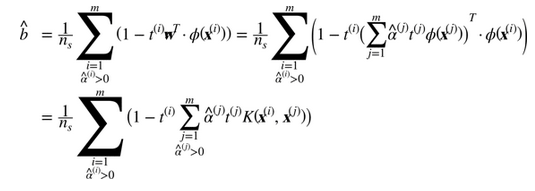
如果你開始感到頭痛,這很正常:因為這是核技巧一個不幸的副作用
在線支持向量機
在結束這一章之前,我們快速地了解一下在線 SVM 分類器(回想一下,在線學習意味著增量地學習,不斷有新實例)。對于線性SVM分類器,一種方式是使用梯度下降(例如使用SGDClassifire)最小化代價函數,如從原始問題推導出的公式 5-13。不幸的是,它比基于 QP 方式收斂慢得多。
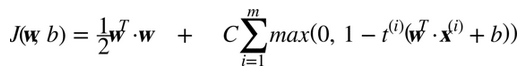
代價函數第一個和會使模型有一個小的權重向量w,從而獲得一個更大的間隔。第二個和計算所有間隔違規的總數。如果樣本位于“街道”上和正確的一邊,或它與“街道”正確一邊的距離成比例,則間隔違規等于 0。最小化保證了模型的間隔違規盡可能小并且少。
Hinge 損失
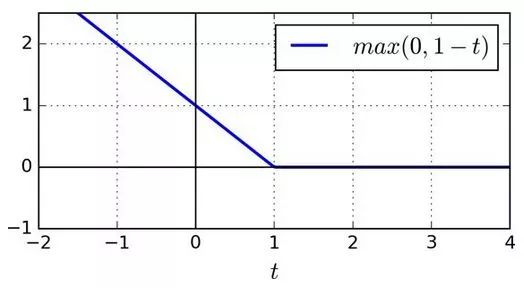
函數max(0, 1–t)被稱為 Hinge 損失函數(如下)。當t≥1時,Hinge 值為 0。如果t<1,它的導數(斜率)為 -1,若t>1,則等于0。在t=1處,它是不可微的,但就像套索回歸(Lasso Regression)(參見 130 頁套索回歸)一樣,你仍然可以在t=0時使用梯度下降法(即 -1 到 0 之間任何值)
我們也可以實現在線核化的 SVM。例如使用“增量和遞減 SVM 學習”或者“在線和主動的快速核分類器”。但是,這些都是用 Matlab 和 C++ 實現的。對于大規模的非線性問題,你可能需要考慮使用神經網絡(見第二部分)
-
分類器
+關注
關注
0文章
152瀏覽量
13175 -
機器學習
+關注
關注
66文章
8382瀏覽量
132444 -
數據集
+關注
關注
4文章
1205瀏覽量
24649
發布評論請先 登錄
相關推薦
【Firefly RK3399試用體驗】之結項——KNN、SVM分類器在SKlearn機器學習工具集中運用
基于四叉樹的分形圖像編碼中的剖分決策函數
采用SVM的網頁分類方法研究
基于信息濃縮的隱私保護分類方法
可檢測網絡入侵的IL-SVM-KNN分類器





 線性SVM分類器通過簡單地計算決策函數
線性SVM分類器通過簡單地計算決策函數











評論