網絡中的信息量呈現指數式增長,隨之帶來了信息過載問題。推薦系統是大數據時代下應運而生的產物,目前已廣泛應用于電商、社交、短視頻等領域。本文將針對推薦系統中基于隱語義模型的矩陣分解技術來進行討論。
NO.1評分矩陣、奇異值分解與Funk-SVD
對于一個推薦系統,其用戶數據可以整理成一個user-item矩陣。矩陣中每一行代表一個用戶,而每一列則代表一個物品。若用戶對物品有過評分,則矩陣中處在用戶對應的行與物品對應的列交叉的位置表示用戶對物品的評分值。這個user-item矩陣被稱為評分矩陣。
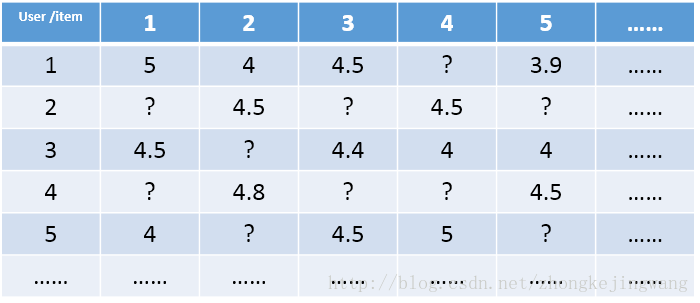
上圖即為評分矩陣的一個例子。其中的?表示用戶還沒有對物品做出評價,而推薦系統最終的目標就是對于任意一個用戶,預測出所有未評分物品的分值,并按分值從高到低的順序將對應的物品推薦給用戶。
說到矩陣分解技術,首先想到的往往是特征值分解(eigendecomposition)與奇異值分解(Singular value decomposition,SVD)。
對于特征值分解,由于其只能作用于方陣,因此并不適合分解評分矩陣這個場景。
而對于奇異值分解,其具體描述為:假設矩陣M是一個m*n的矩陣,則一定存在一個分解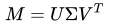
于是我們馬上能得到一個解決方案:對原始評分矩陣M做奇異值分解,得到U、V及Σ,取Σ中較大的k類作為隱含特征,則此時M(m*n)被分解成U(m*k) Σ(k*k)V(k*n),接下來就可以直接使用矩陣乘法來完成對原始評分矩陣的填充。但是實際上,這種方法存在一個致命的缺陷——奇異值分解要求矩陣是稠密的。也就是說SVD不允許待分解矩陣中存在空白的部分,這一開始就與我們的問題所沖突了。
當然,也可以想辦法對缺失值先進行簡單的填充,例如使用全局平均值。然而,即使有了補全策略,在實際應用場景下,user和item的數目往往是成千上萬的,面對這樣的規模傳統SVD算法O(n^3)的時間復雜度顯然是吃不消的。因此,直接使用傳統SVD算法并不是一個好的選擇。
既然傳統SVD在實際應用場景中面臨著稀疏性問題和效率問題,那么有沒有辦法避開稀疏問題,同時提高運算效率呢?
實際上早在06年,Simon Funk就提出了Funk-SVD算法,其主要思路是將原始評分矩陣M(m*n)分解成兩個矩陣P(m*k)和Q(k*n),同時僅考察原始評分矩陣中有評分的項分解結果是否準確,而判別標準則是均方差。
即對于矩陣M(m*n),我們想辦法將其分解為P(m*k)、Q(k*n),此時對于原始矩陣中有評分的位置MUI來說,其在分解后矩陣中對應的值就是
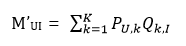
那么對于整個評分矩陣而言,總的損失就是
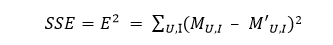
只要我們能想辦法最小化上面的損失SSE,就能以最小的擾動完成對原始評分矩陣的分解,在這之后只需要用計算M’ 的方式來完成對原始評分矩陣的填充即可。(達觀數據 周顥鈺)
這種方法被稱之為隱語義模型(Latent factor model,LFM),其算法意義層面的解釋為通過隱含特征(latent factor)將user興趣與item特征聯系起來。
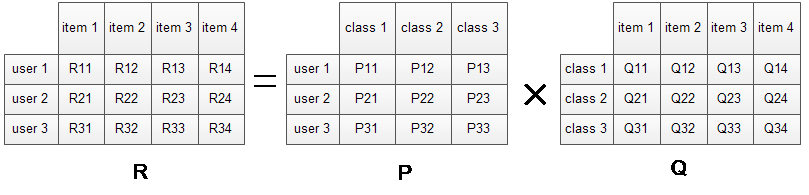
對于原始評分矩陣R,我們假定一共有三類隱含特征,于是將矩陣R(3*4)分解成用戶特征矩陣P(3*3)與物品特征矩陣Q(3*4)。考察user1對item1的評分,可以認為user1對三類隱含特征class1、class2、class3的感興趣程度分別為P11、P12、P13,而這三類隱含特征與item1相關程度則分別為Q11、Q21、Q31。
回到上面的式子
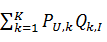
可以發現用戶U對物品I最終的評分就是由各個隱含特征維度下U對I感興趣程度的和,這里U對I的感興趣程度則是由U對當前隱含特征的感興趣程度乘上I與當前隱含特征相關程度來表示的。
于是,現在的問題就變成了如何求出使得SSE最小的矩陣P和Q。
NO.2隨機梯度下降法
在求解上文中提到的這類無約束最優化問題時,梯度下降法(Gradient Descent)是最常采用的方法之一,其核心思想非常簡單,沿梯度下降的方向逐步迭代。梯度是一個向量,表示的是一個函數在該點處沿梯度的方向變化最快,變化率最大,而梯度下降的方向就是指的負梯度方向。
根據梯度下降法的定義,其迭代最終必然會終止于一階導數(對于多元函數來說則是一階偏導數)為零的點,即駐點。對于可導函數來說,其極值點一定是駐點,而駐點并不一定是極值點,還可能是鞍點。另一方面,極值點也不一定是最值點。下面舉幾個簡單的例子。
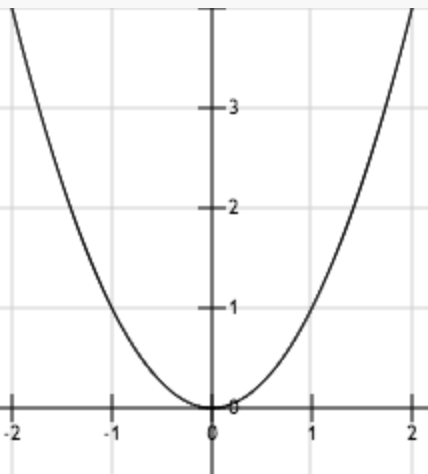
上圖為函數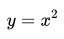 。從圖中可以看出,函數唯一的駐點 (0,0)為其最小值點。
。從圖中可以看出,函數唯一的駐點 (0,0)為其最小值點。
上圖為函數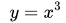 。其一階導數為
。其一階導數為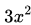 ,從而可知其同樣有唯一駐點(0,0)。從圖中可以看出,函數并沒有極值點。
,從而可知其同樣有唯一駐點(0,0)。從圖中可以看出,函數并沒有極值點。
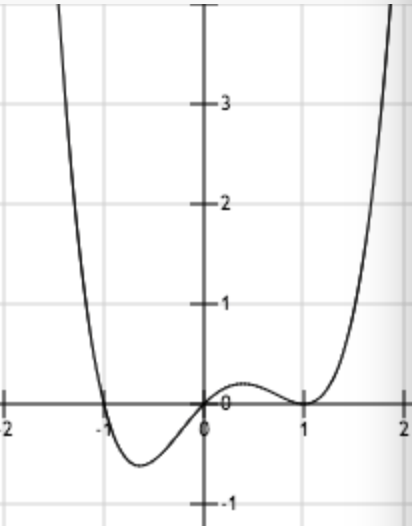
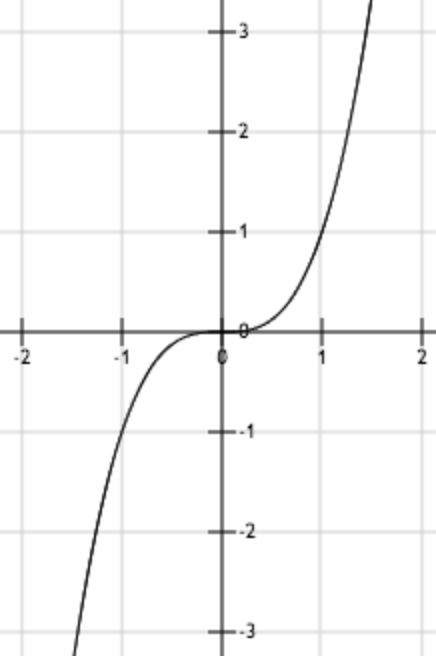
上圖為函數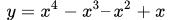

上圖為函數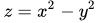
從上面幾幅函數圖像中可以看出梯度下降法在求解最小值時具有一定的局限性,用一句話概括就是,目標函數必須是凸函數。關于凸函數的判定,對于一元函數來說,一般是求二階導數,若其二階導數非負,就稱之為凸函數。對于多元函數來說判定方法類似,只是從判斷一元函數的單個二階導數是否非負,變成了判斷所有變量的二階偏導數構成的黑塞矩陣(Hessian Matrix)是否為半正定矩陣。判斷一個矩陣是否半正定可以判斷所有特征值是否非負,或者判斷所有主子式是否非負。
回到上面funk-svd的最優化問題上來。經過一番緊張刺激的計算之后,可以很遺憾地發現,我們最終的目標函數是非凸的。這就意味著單純使用梯度下降法可能會找到極大值、極小值或者鞍點。這三類點的穩定性按從小到大排列依次是極大值、鞍點、極小值,考慮實際運算中,浮點數運算都會有一定的誤差,因此最終結果很大幾率會落入極小值點,同時也有落入鞍點的概率。而對于極大值點,除非初始值就是極大值,否在幾乎不可能到達極大值點。
為了從鞍點和極小值點中脫出,在梯度下降法的基礎上衍生出了各式各樣的改進算法,例如動態調整步長(即學習率),利用上一次結果的動量法,以及隨機梯度下降法(Stochastic Gradient Descent, SGD)等等。實際上,這些優化算法在當前最火熱的深度學習中也占據著一席之地,例如adagrad、RMSprop,Adam等等。而本文則將主要介紹一下隨機梯度下降法。(達觀數據 周顥鈺)
隨機梯度下降法主要是用來解決求和形式的優化問題,與上面需要優化的目標函數一致。其思想也很簡單,既然對于求和式中每一項求梯度很麻煩,那么干脆就隨機選其中一項計算梯度當作總的梯度來使用好了。
具體應用到上文中的目標函數
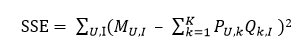
SSE是關于P和Q的多元函數,當隨機選定U和I之后,需要枚舉所有的k,并且對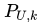
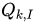
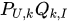
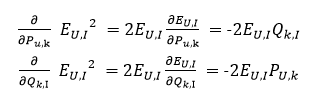
在實際的運算中,為了P和Q中所有的值都能得到更新,一般是按照在線學習的方式選擇評分矩陣中有分數的點對應的U、I來進行迭代。
值得一提的是,上面所說的各種優化都無法保證一定能找到最優解。有論文指出,單純判斷駐點是否是局部最優解就是一個NPC問題,但是也有論文指出SGD的解能大概率接近局部最優甚至全局最優。
另外,相比于利用了黑塞矩陣的牛頓迭代法,梯度下降法在方向上的選擇也不是最優的。牛頓法相當于考慮了梯度的梯度,所以相對更快。而由于其線性逼近的特性,梯度下降法在極值點附近可能出現震蕩,相比之下牛頓法就沒有這個問題。
但是在實際應用中,計算黑塞矩陣的代價是非常大的,在這里梯度下降法的優勢就凸顯出來了。因此,牛頓法往往應用于一些較為簡單的模型,如邏輯回歸。而對于稍微復雜一些的模型,梯度下降法及其各種進化版本則更受青睞。(達觀數據 周顥鈺)
NO.3基于Funk-SVD的改進算法
到這一步為止,我們已經能通過SGD找到一組分解方案了,然而對于填充矩陣的FunkSVD算法本身而言,目前這個形式是否過于簡單了一些呢?
實際上,在Funk-SVD被提出之后,出現了一大批改進算法。本文將介紹其中某些經典的改進思路。
1
正則化
對于所有機器學習算法而言,過擬合一直是需要重視的一個問題,而加入正則化項則是防止過擬合的經典處理方法。對于上面的Funk-SVD算法而言,具體做法就是在損失函數后面加入一個L2正則項,即
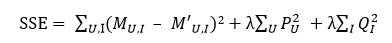
其中,λ為正則化系數,而整個求解過程依然可以使用隨機梯度下降來完成。
2
偏置
考察式子
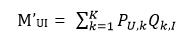
可以發現這個式子表明用戶U對物品 I 的評分全部是由U和I之間的聯系帶來的。然而實際上,有很多性質是用戶或者物品所獨有的。比如某個用戶非常嚴苛,不論對什么物品給出的分數都很低,這僅僅與用戶自身有關。
又比如某個物品非常精美,所有用戶都會給出較高的分數,這也僅僅與物品自身有關。因此,只通過用戶與物品之間的聯系來預測評分是不合理的,同時也需要考慮到用戶和物品自身的屬性。于是,評分預測的公式也需要進行修正。不妨設整個評分矩陣的平均分為σ,用戶U和物品I的偏置分別為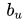
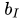
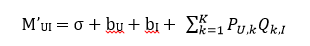
同時,誤差E除了由于M‘計算方式帶來的變化之外,也同樣需要加入U和I偏置的正則項,因此最終的誤差函數變成了
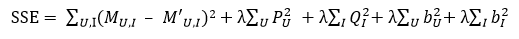
3
隱式反饋
對于實際的應用場景中,經常有這樣一種情況:用戶點擊查看了某一個物品,但是最終沒有給出評分。
實際上,對于用戶點擊查看物品這個行為,排除誤操作的情況,在其余的情況下可以認為用戶被物品的描述,例如貼圖或者文字描述等所吸引。這些信息我們稱之為隱式反饋。事實上,一個推薦系統中有明確評分的數據是很少的,這類隱式數據才占了大頭。
可以發現,在我們上面的算法當中,并沒有運用到這部分數據。于是對于評分的方法,我們可以在顯式興趣+偏置的基礎上再添加隱式興趣,即
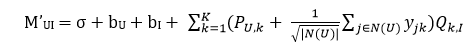
其中N(U)表示為用戶U提供了隱式反饋的物品的集合。這就是svd++算法。
此時的損失函數也同樣需要加上隱式興趣的正則項,即
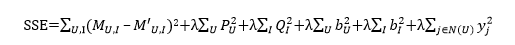
4
對偶算法
在上面的svd++中,我們是基于用戶角度來考慮問題的,很明顯我們同樣可以基于物品的角度來考慮問題。具體來說就是
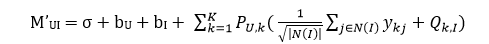
其中 N(I)表示為物品I提供了隱式反饋的用戶的集合。類似地,在損失函數中也需要加上隱式興趣的正則項。
在實際運用中,可以將原始的svd++得到的結果與對偶算法得到的結果進行融合,使得預測更加準確。然而相比起物品的數目,用戶的數目往往是要高出幾個量級的,因此對偶算法在儲存空間和運算時間的開銷上都將遠高于原始的svd++,如何在效率和準確度之間找到平衡也是一個需要思考的問題。(達觀數據 周顥鈺)
NO.4請因子分解機
矩陣分解的思想除了直接應用在分解評分矩陣上之外,其思想也能用在其他地方,接下來介紹的因子分解機(Factorization Machine,FM)就是一個例子。
對于經典的邏輯回歸算法,其sigmoid函數中的項實際上是一個線性回歸
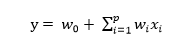
在這里我們認為各個特征之間是相互獨立的,而事實上往往有些特征之間是相互關聯、相互影響的。因此,就有必要想辦法捕捉這些特征之間的相互影響。簡單起見,先只捕捉二階的關系,即特征之間兩兩之間的相互影響。具體反映到回歸公式上,即為
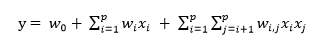
具體來說就是使用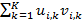
NO.5與DNN的結合
深度學習無疑是近幾年來最熱門的機器學習技術。注意到隱語義模型中,隱含特征與深度學習中的embedding實際上是一回事,那么是否有可能借助DNN來幫助我們完成矩陣分解的工作呢?
實際上,在YouTube的文章《Deep neural networks for YouTube recommendations》中,就已經有了相關技術的應用。
上圖是YouTube初排模型的圖示。具體的流程為:首先通過nlp技術,如word2vec,預訓練出所有物品的向量I表示;然后對于每一條用戶對物品的點擊,將用戶的歷史點擊、歷史搜索、地理位置信息等信息經過各自的embedding操作,拼接起來作為輸入,經過MLP訓練后得到用戶的向量表示U;而最終則是通過 softmax 函數來校驗U*I的結果是否準確。
相比于傳統的矩陣分解算法,使用DNN能為模型帶來非線性的部分,提高擬合能力。另一方面,還可以很方便地加入各式各樣的特征,提高模型的準確度。(達觀數據 周顥鈺)
NO.6矩陣分解的優缺點
矩陣分解有如下優點:
能將高維的矩陣映射成兩個低維矩陣的乘積,很好地解決了數據稀疏的問題;
具體實現和求解都很簡潔,預測的精度也比較好;
模型的可擴展性也非常優秀,其基本思想也能廣泛運用于各種場景中。
相對的,矩陣分解的缺點則有:
可解釋性很差,其隱空間中的維度無法與現實中的概念對應起來;
訓練速度慢,不過可以通過離線訓練來彌補這個缺點;
實際推薦場景中往往只關心topn結果的準確性,此時考察全局的均方差顯然是不準確的。
NO.7總結
矩陣分解作為推薦系統中的經典模型,已經經過了十幾年的發展,時至今日依然被廣泛應用于推薦系統當中,其基本思想更是在各式各樣的模型中發揮出重要作用。但是對于推薦系統來說,僅僅有一個好的模型是遠遠不夠的。影響推薦系統效果的因素非常之多。想要打造一個一流的推薦系統,除了一個強大的算法模型之外,更需要想方設法結合起具體業務,不斷進行各種嘗試、升級,方能取得最終的勝利。
參考文獻
【1】Simon Funk, http://sifter.org/~simon/journal/20061211.html
【2】Koren, Yehuda, Robert Bell, and Chris Volinsky. "Matrix factorization techniques for recommender systems."Computer42.8 (2009).
【3】Jahrer, Michael, and Andreas T?scher. "Collaborative filtering ensemble."Proceedings of the 2011 International Conference on KDD Cup 2011-Volume 18. JMLR. org, 2011.
【4】Rendle, Steffen. "Factorization machines."Data Mining (ICDM), 2010 IEEE 10th International Conference on. IEEE, 2010.
【5】Covington, Paul, Jay Adams, and Emre Sargin. "Deep neural networks for youtube recommendations."Proceedings of the 10th ACM Conference on Recommender Systems. ACM, 2016.
-
推薦系統
+關注
關注
1文章
43瀏覽量
10073 -
矩陣分解
+關注
關注
1文章
13瀏覽量
3671
原文標題:技術干貨丨想寫出人見人愛的推薦系統,先了解經典矩陣分解技術
文章出處:【微信號:AI_Thinker,微信公眾號:人工智能頭條】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
矩陣分解,不知是用的什么分解算法
基于CORDIC技術的無開方無除法的MQR陣分解方法
非負矩陣集分解
快速高效的實現浮點復數矩陣分解
基于評分相似性的群稀疏矩陣分解推薦算法
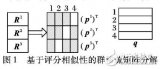
利用CUR矩陣分解提高特征選擇與矩陣恢復能力
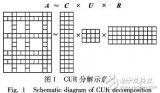
基于矩陣分解的手機APP推薦
基于低秩矩陣分解在母線中應用
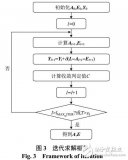
基于Spark的矩陣分解并行化算法
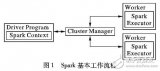




 推薦系統中的矩陣分解技術
推薦系統中的矩陣分解技術











評論