在本文中,我們將了解一致性哈希是什么、為什么它是可擴展的分布式系統架構中的一個必要工具。
此外,我們將探究可用于大規模實施該算法的數據結構。最后,我們還將探究一個實際例子。
一致性哈希到底是什么?
還記得你在大學里學到的那種傳統的樸素哈希方法嗎?使用哈希函數,我們確保計算機程序所需的資源能夠高效地存儲在內存中,從而確保內存中的數據結構均勻地加載。
我們還確保該資源存儲策略同樣使得信息檢索更高效,因而使程序運行起來更快。
經典的哈希方法使用哈希函數來生成偽隨機數,然后除以內存空間的大小,將隨機標識符轉變成可用空間內的一個位置。
結果看起來如下:location = hash(key)mod size。
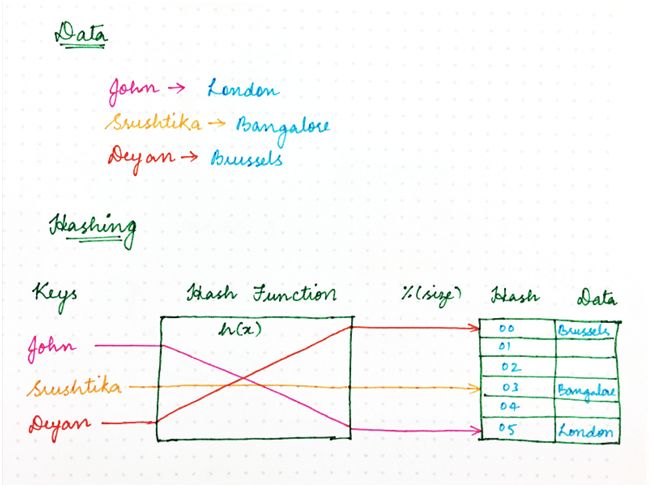
圖 1
那么,我們為什么不使用同一方法來處理網絡上的請求?
在各種程序、計算機或用戶向多個服務器節點請求一些資源的場景下,我們需要一種機制將請求均勻地映射到可用的服務器節點,從而確保負載均衡,并且保持一致的性能。
我們不妨將服務器節點視為一個或多個請求可以映射到的占位符,現在不妨后退一步。
在經典哈希方法中,我們總是假設:內存位置的數量是已知的,而且這個數永遠不變。
比如我們通常在一天內擴大或縮小集群規模,還要處理突如其來的故障。但是如果我們考慮上述場景,就無法保證服務器節點的數量保持不變。
如果其中一個突然出現故障,該怎么辦?使用樸素哈希方法,我們最終需要重新計算每一個鍵的哈希值,因為新映射依賴節點數量/內存位置,如下所示:
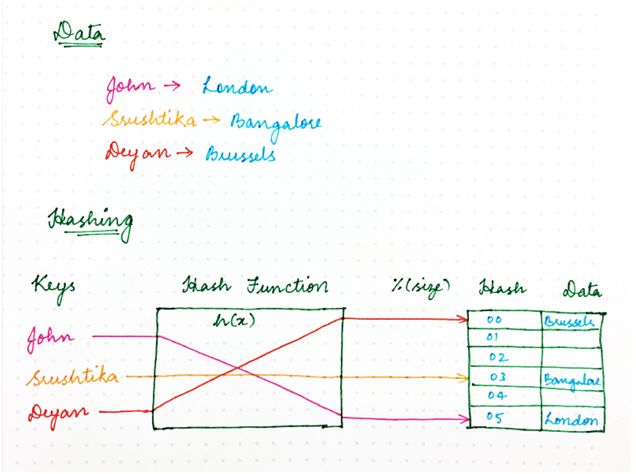
圖 2:之前
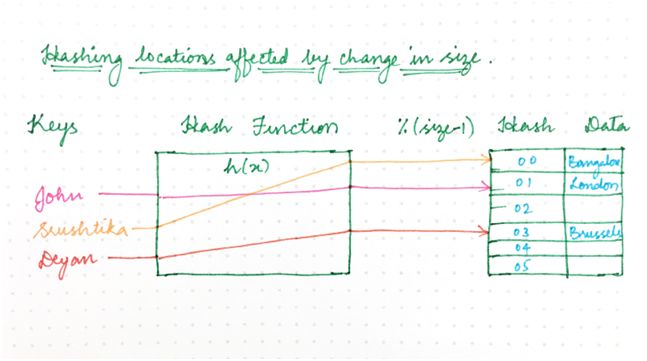
圖 3:之后
只是重新計算哈希值的分布式系統(每個鍵的位置都移動)存在一個問題,那就是每個節點上都存儲了狀態。
比如說,集群規模的微小變化可能導致大量的工作,以便重新調整集群內的所有數據。
集群規模變大后,這就無以為繼,因為每個哈希變更(hash change)所需的工作量隨集群規模呈線性增長。這時,一致性哈希這個概念有了用武之地。
一致性哈希到底是什么?可以這樣來描述:
它表示某種虛擬環結構(名為哈希環,HashRing)中的資源請求者(我們在本文中簡稱為“請求”)和服務器節點。
位置數量不再固定,但是環被認為有無限數量的點,服務器節點可以放置在該環上的隨機位置。
當然,再次選擇該隨機數可以使用哈希函數來完成,但是除以可用位置數量的第二步被跳過,因為它不再是一個有限數。
請求即用戶、計算機或無服務器程序,它們類似于經典哈希方法中的鍵,也使用同樣的哈希函數放置在同一個環上。
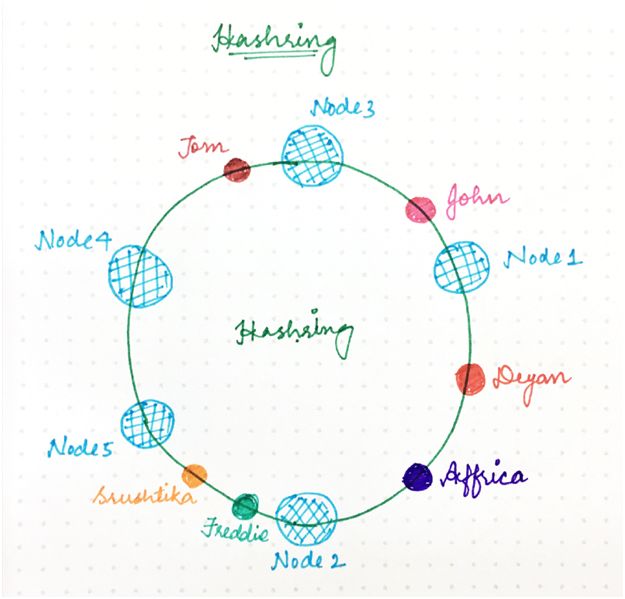
圖 4
那么,如何決定哪個請求將由哪個服務器節點來處理?如果我們假設環是有序的,以便環的順時針遍歷與位置地址的遞增順序對應,那么每個請求可以由最先出現在該順時針遍歷中的那個服務器節點來處理。
也就是說,地址高于請求地址的第一個服務器節點負責處理該請求。如果請求地址高于最高尋址節點,它由最小地址的服務器節點來處理,因為環遍歷以圓形方式進行。如下圖所示:
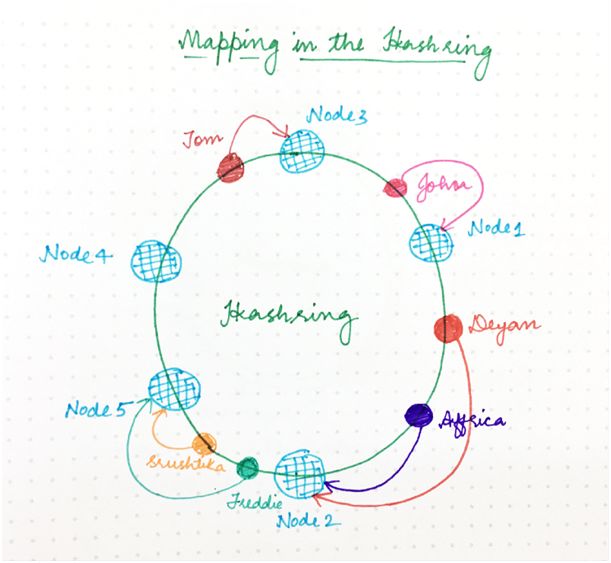
圖 5
從理論上來說,每個服務器節點“擁有”哈希環的一個區間,進入該區間的任何請求將由同一服務器節點來處理。
現在,如果其中一個服務器節點(比如節點 3)出現故障,下一個服務器節點的區間就變寬,進入該區間的任何請求都將進入到新的服務器節點,該怎么辦?
那就需要重新分配的是僅僅這一個區間(與出現故障的服務器節點對應),哈希環的其余部分和請求/節點分配仍然不受影響。
這與經典哈希技術形成了對比:哈希表大小的變更實際上干擾了所有映射。
由于一致性哈希,只有一部分請求(相對于環分配因子)會受到特定的環變更的影響。(之所以出現環變更,是由于添加或刪除節點導致一些請求/節點映射發生了變化。)
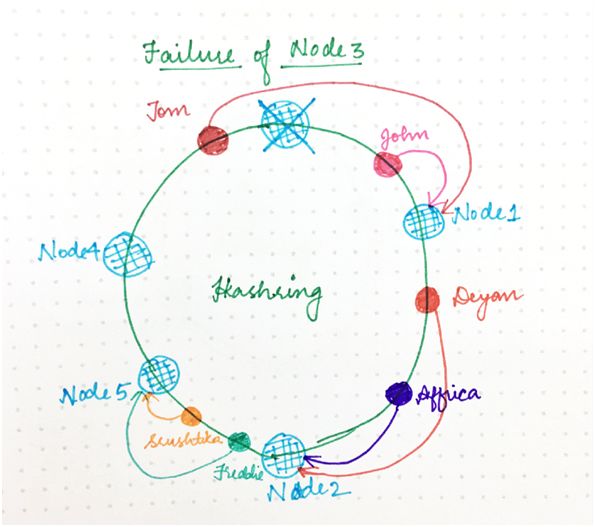
圖 6
如何高效地實施一致性哈希算法?
我們弄清楚了哈希環是什么,現在需要實施下列部分讓它發揮作用:
從我們的哈希空間到集群中節點的映射,讓我們得以找到負責某個請求的節點。
針對解析到某個節點的集群的那些請求的集合。之后,這將讓我們得以搞清楚哪些哈希值受到添加或刪除某個節點的影響。
映射
為了完成上面第一個部分,我們需要下列部分:
在給出請求標識符的情況下,計算環中位置的哈希函數。
搞清楚哪個節點與哈希請求對應的方法。
為了搞清楚與某個請求對應的節點,我們可以使用一種簡單的數據結構來進行表示,包括下列部分:
與環中節點對應的哈希數組。
用于查找與某個請求對應的節點的圖(哈希表)。
這實際上是有序圖的一種原始表示。想找到負責上述結構中某個哈希值的節點,我們需要:
執行修改后的二進制搜索,查找數組中等于或大于(≥)所要查找的哈希值的第一個節點/哈希值。
查找與圖中已找到的節點/哈希值對應的節點。
添加或刪除節點
正如我們在文章開頭看到,添加新節點時,必須將含有各種請求的哈希環的某些部分分配給該節點。
反過來,刪除節點時,已分配給該節點的請求需要由另外某個節點來處理。
我們如何查找受環變更影響的那些請求?一種解決方案是遍歷分配給節點的所有請求。
對于每個請求,我們確定它是否屬于已出現的環變更的范圍內,必要時將它移到其他位置。
不過,執行此操作所需的工作量隨分配給某個節點的請求數量的增加而增加。由于節點數量增加后,出現的環變更的數量往往增加,情況變得更糟。
在最糟糕的情況下,由于環變更常常與局部故障有關,因此與環變更相關的瞬時負載也可能加大其他節點同樣受影響的可能性,可能導致整個系統出現連鎖反應問題。
為了解決這個問題,我們希望請求的重新定位盡可能高效。理想情況下,我們將所有請求存儲在這樣一種數據結構中:便于我們找到受環上任何位置的單一哈希變更影響的那些請求。
高效地查找受影響的哈希值
往集群添加節點或從集群刪除節點將改變在環的一些部分分配請求,我們稱之為受影響的區間(affected range)。如果我們知道受影響區間的界限,就能夠將請求移到正確的位置。
想找到受影響區間的邊界,從已添加或已刪除的節點的哈希值 H 開始,我們就能從 H 開始沿環向后移動(圖中逆時針),直至找到另一個節點。
不妨稱該節點的哈希值為 S(開始值)。該節點逆時針的請求將定位到它,那樣這些請求不會受影響。
請注意:這只是簡單描述了發生的情況;實際上,結構和算法更加復雜,因為我們使用大于 1 的復制因子和專門的復制策略(只有一小部分的節點適用于任何特定的請求)。
區間中的放置哈希值介于已找到的節點與已添加(或已刪除)的節點之間的請求是需要移動的請求。
高效地查找受影響區間中的請求
一種解決方案就是遍歷與某個節點對應的所有請求,并更新哈希值在該區間內的請求。
在 JavaScript 中可能看起來像這樣:
for(constrequestofrequests){if(contains(S,H,request.hash)){/*therequestisaffectedbythechange*/request.relocate();}}functioncontains(lowerBound,upperBound,hash){constwrapsOver=upperBound=lowerBound;constbelowUpper=upperBound>=hash;if(wrapsOver){returnaboveLower||belowUpper;}else{returnaboveLower&&belowUpper;}}
由于環是圓形的,光查找 S <= r
只要請求數量比較少,或如果節點的添加或刪除比較少見,迭代某個節點上的所有請求就行。
不過,某個節點處的請求數量增加后,所需的工作量隨之增加;更糟糕的是,隨著節點數量增加,無論是由于自動擴展還是故障切換,環變更往往會更頻繁地出現,從而觸發系統上的同步負載重新均衡請求。
在最糟糕的情況下,與此相關的負載可能加大其他節點上出現故障的可能性,可能導致整個系統出現連鎖反應問題。
為了應對這種情況,我們還可以將請求存儲在與前面討論的數據結構類似的單獨的環數據結構中。在此環中,哈希直接映射到位于該哈希值的請求。
然后我們可以執行下列操作,找到區間內的請求:
找到區間開始值 S 后的第一個請求。
順時針迭代,直至找到哈希值超出區間的請求。
重新找到區間內的那些請求。
針對特定的哈希更新而需要迭代的請求數量平均為 R/N,其中 R 是位于節點區間內的請求數量,N 是環中哈希值的數量,假設請求均勻地分配。
下面用一個實際的例子來介紹上述解釋。
假設我們有一個集群含有兩個節點:A 和 B。不妨為這每個節點隨機生成一個“放置哈希值”(假設是 32 位哈希值)。
于是我們得到:
A:0x5e6058e5
B:0xa2d65c0
這將節點放在一個假想環上,其中數字 0x0、0x1、0x2......連續放置到 0xffffffff。
由于節點 A 有哈希值 0x5e6058e5,因此它負責哈希進入到區間 0xa2d65c0+1 直到 0xffffffff 以及從 0x0 直到 0x5e6058e5 的任何請求,如下所示:
圖 7
另一方面,B 負責區間 0x5e6058e5+1 直到 0xa2d65c0。因此,整個哈希空間是分布式的。
從節點到哈希的這種映射需要與整個集群共享,以便環計算的結果始終相同。因此,需要特定請求的任何節點都可以查明其所在位置。
假設我們想要查找(或創建)擁有標識符“bobs.blog@example.com”的請求:
我們計算標識符的哈希值 H,比如 0x89e04a0a。
我們查看環,找到哈希值大于 H 的第一個節點,這里恰好是 B。
因此 B 是負責該請求的節點。如果我們再次需要該請求,將重復上述步驟,再次登陸到同一個節點,它有我們所需的狀態。
這個例子有點過于簡單,實際上,每個節點有一個哈希可能會很不公平地分配負載。
你可能已注意到,在這個例子中,B 負責環的(0xa2d656c0-0x5e6058e5)/232 = 26.7%,而 A 負責其余部分。理想情況下,每個節點將負責環的相等部分。
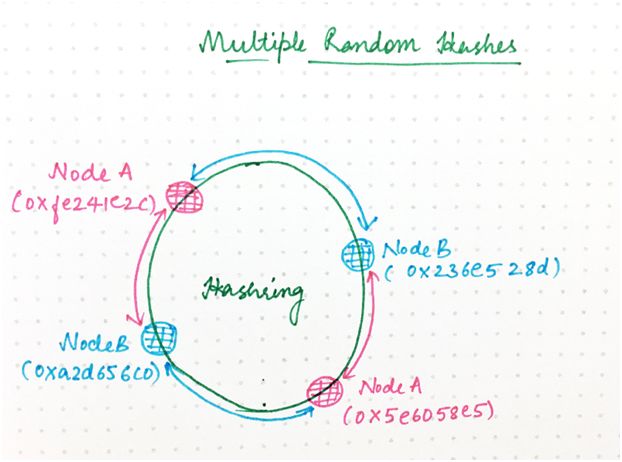
讓這更公平的一種方法是,為每個節點生成多個隨機哈希值,如下所示:
圖 8
實際上,我們發現這個結果仍然不能令人滿意,于是我們將環分成 64 個大小同等的段,確保每個節點的哈希值放在每個段的某個位置;不過,這方面的細節不重要。
目的只是想確保每個節點負責環的同等部分,從而使負載均勻地分配。(每個節點有多個哈希值的另一個優點是,可以逐漸將哈希值添加到環中或從環中移除,以免負載突然猛增。)
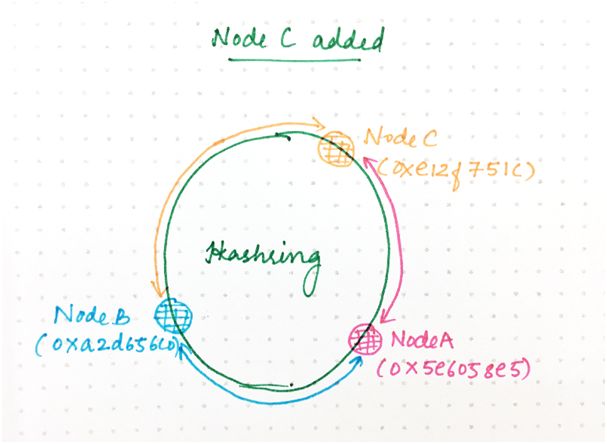
假設現在我們向環添加一個名為 C 的新節點,我們為 C 生成隨機哈希值:
A:0x5e6058e5
B:0xa2d65c0
C:0xe12f751c
0xa2d65c0+1 和 0xe12f751c(用于哈希到 A)之間的環空間現在被委托給 C。所有的其他請求將繼續哈希到與之前相同的那個節點。
為了處理這種權力轉移,該區間內已經在 A 上的所有請求都需要將其所有狀態轉移到 C。
圖 9
你現已了解了為什么分布式系統中需要哈希以均勻地分配負載。然而需要一致性哈希,確保一旦出現環變更,集群中只需要最小的工作量。
此外,節點需要存在于環上的多個位置,確保從統計學上來說負載更可能更均勻地分配。
為每個環變更迭代整個哈希環效率很低下。隨著分布式系統的規模不斷擴大,勢必需要一種更高效的方法來查明什么發生了變更,從而盡可能減小環變更對性能帶來的影響。這就需要新的索引和數據類型來解決這個問題。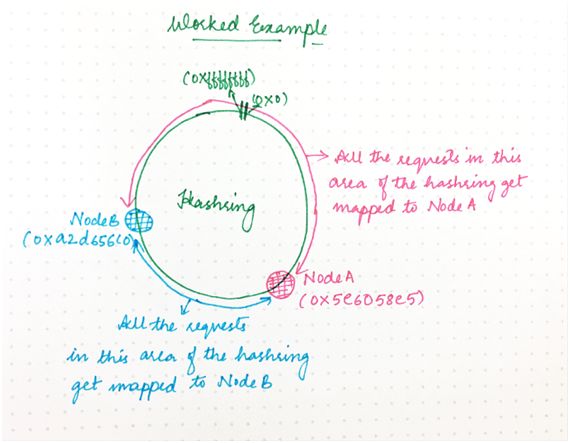
-
算法
+關注
關注
23文章
4552瀏覽量
92021 -
架構
+關注
關注
1文章
501瀏覽量
25374 -
分布式系統
+關注
關注
0文章
143瀏覽量
19164
原文標題:一致性哈希算法很難?看完這篇全懂了
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
一行代碼,保障分布式事務一致性—GTS:微服務架構下分布式事務解決方案
一文讀懂分布式架構知識體系(內含超全核心知識大圖)
分布式一致性算法Yac
基于消息通信的分布式系統最終一致性平臺

分布式大數據不一致性檢測
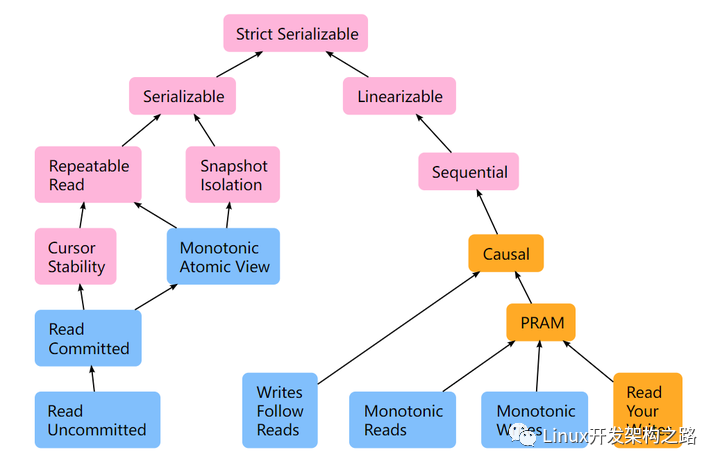
分布式系統的CAP和數據一致性模型
基于自觸發一致性算法的分布式分層控制策略
一種更安全的分布式一致性算法選舉機制

最終一致性是現在大部分高可用的分布式系統的核心思路
深入理解數據備份的關鍵原則:應用一致性與崩潰一致性的區別





 一致性哈希是什么?為什么它是可擴展的分布式系統架構的一個必要工具
一致性哈希是什么?為什么它是可擴展的分布式系統架構的一個必要工具











評論