摘要:雖然一致性幾何繞射理論(UTD)理論上可以應用于由非均勻有理B樣條(NURBS)建模的任意形狀的曲面,但UTD表面衍射場的計算中有一個巨大挑戰,即難以確定爬行波在任意形狀的NURBS表面上傳播的測地線路徑。在微分幾何中,測地路徑滿足測地微分方程(GDE)。因此,引入了一種通用且高效的自適應變量歐拉法來解決任意形狀的NURBS曲面上的GDE。與傳統的歐拉法相比,所提出的方法采用形狀因子(SF)ξ來有效提高跟蹤精度,并擴展了UTD在實際工程中的應用。 算法的有效性和有用性可以通過數值計算結果進行驗證。
0 引言
在高頻電磁問題中,一致性幾何繞射理論(UTD)應用非常廣泛[1],例如目標散射特性預估。因此,在準確獲得目標表面UTD繞射場問題上,表面爬行射線波追蹤起著非常大的作用[2]。所以,首先要進行目標表面爬行波追蹤(測地線軌跡)。但是,實際上除了一些典型形體能夠直接得到測地線微分方程(GDE)外,在任意形狀的光滑物體表面如何測定測地線軌跡是一個巨大的挑戰。
JHA R M[3-5]提出了Geodesic Constant解析方法,但只在一般的拋物旋轉面適用。通常地,在工程應用上,很多目標被看作如木板、圓柱、圓錐和球等一些已經有爬行波尋跡解析解的典型形體。但很難用這些典型形體去估計復雜形體,這似乎就限制了UTD方法的應用。
因此,需要介紹一下數值爬行波追蹤算法,該方法基于離散三角面剖分模型表面,但是不能直接應用于UTD算法[6]。除了用離散三角形面片建立復雜模型,它還可以描述NURBS曲面。而且,NURBS曲面由于它的高精度、少面片的特性,被引用到高頻電磁分析領域。當目標用NURBS曲面表示后,測地線軌跡可由GDE求解直接獲得。所以,一些數值方法被用來計算GDE。為了獲得NURBS曲面上的爬行波軌跡[7],歐拉方法效率高但是精度低,精度依賴于剖分面片外形,對于任意形狀模型可能會失效。
為了提高在任意形狀NURBS表面爬行波追蹤的準確性和效率,本文提出了一種基于新型自適應變步長歐拉法的爬行波跟蹤算法。由于自適應變步長歐拉方法是基于傳統的歐拉法,從而保證了效率;并在數值迭代求解GDE的過程中引進形狀因子ξ,離散的步長可以及時自適應地糾正。因此,與傳統的歐拉法相比,該方法可以很容易地保證其準確性在任意形狀的NURBS表面上的爬行光線跟蹤。也就是說,它更適合于工程應用。
1 任意形狀目標NURBS曲面建模
非均勻有理B樣條(Non-Uniform Rational B-Splines,NURBS)曲面是非均勻B樣條曲面的有理推廣。它被定義為:

u、v參數域映射到3個空間可以在圖1中看到。
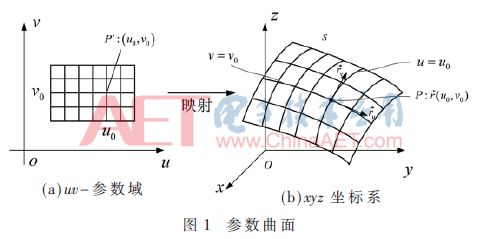


下面在圖2中給出3個NURBS建模結果。其中圓柱的表面是均勻網格表面,而其他表面是不均勻網格表面。
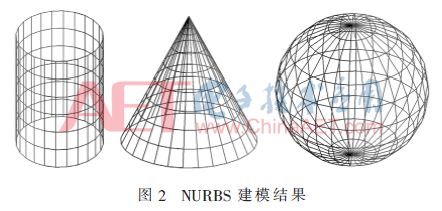
2 任意NURBS曲面表面的爬行波追蹤算法
對于源點和觀察點的位置,光滑曲面表面的繞射問題有3種類型:(1)源點和觀察點都不在表面且遠離表面,這種情況屬于光滑曲面散射問題;(2)源點在曲面上,觀察點遠離表面,此時為光滑曲面輻射問題;(3)源點與觀察點都在表面上,這就屬于耦合問題[10]。
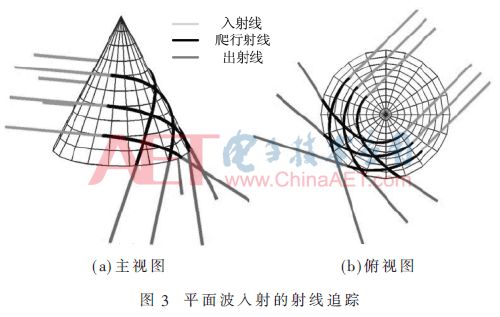
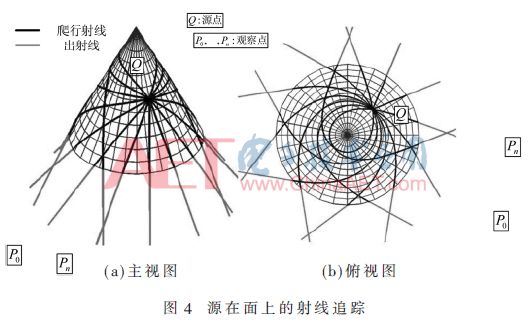
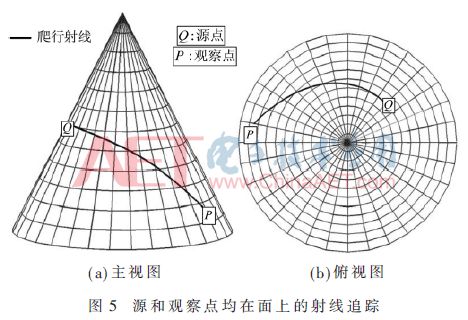
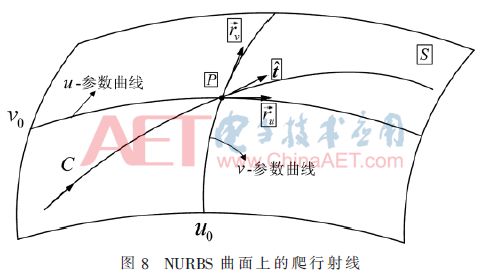
所以,射線追蹤也有3種類型,根據圖3~圖5所示,在所有這些情況下,表面上的射線軌跡稱為爬行波,其被約束沿著測地線傳播。本文主要關注爬行波的射線追蹤,因為它是射線追蹤過程中最困難的一部分。
2.1 爬行波的入射點和出射點
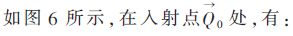
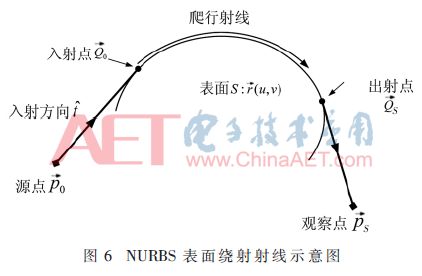

根據這兩個方程可以求解出NURBS曲面上大量的入射點與出射點。
2.2 基于自適應變步長歐拉法求解射線追蹤GDE
由于任意形狀的表面上的爬行射線的路徑滿足GDE,因此可以將爬行射線的問題改為求解GDE的問題。一般來說,通過歐拉法求解GDE是一種簡單快捷的方法。但是根據研究,在大多數情況下由于傳統的歐拉法精度低,穩定性不好,導致求解效果不好。
對于非線性問題,基本上需要步進控制校正程序。因此,本文中,為提高光線跟蹤的準確性并確保效率,提出了自適應變步長歐拉方法來求解GDE。
GDE方程如下:
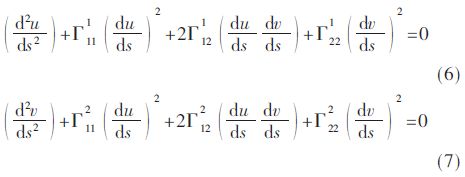

其中,h是兩個相鄰離散點之間的步長,并且確定它是非常重要的。ξ是形狀因子(SF),用來自適應地控制每個離散步長。而ξ的值受制于對象的形狀,關于ξ的更多細節將在2.3節中給出。
在數值計算中,可以計算多個離散點(ui,vi)來表示爬行波,i=0,1,2…。因此,根據離散化,上式可以重寫為:

由式(13)可知,(ui+2,vi+2)能用(ui+1,vi+1)、(ui,vi)及ξi+1,i推導而出。必須計算出爬行射線最初的兩個坐標(u0,v0)、(u1,v1)及ξ1,0,才能遞推出整個爬行射線。
可以通過方程(4)獲得第一個點Q0(u0,v0),然后由微分幾何,第二個點可由Q0在u,v各自方向切向量之和近似表示,如圖7所示。

這里第二個點表示為:

形狀因子的一般表達式在2.3節中給出。根據表達式,可以確定得到ξ1,0。計算出(u0,v0)、(u1,v1)及ξ1,0后,(ui,vi)可以根據式(12)隨著i的增加逐步迭代算出。
2.3 形狀因子?孜的推導
微分方程的精度與步長h有關,步長越小精度越高。然而,在迭代求解爬行波射線軌跡上的離散點的過程中,算法效率因離散點數的增加而減小,而且,離散點越多,累積誤差越大,可能導致錯誤的結果。
顯然,為了逼近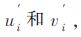
但是在實際情況中,無法得知確定的(u(s),v(s))表達式,所以導致離散點無法合理提取。于是本文提出用形狀因子ξ來反映參數變化,用于確定離散步長。用ξ的離散值ξi+1,i來表示爬行射線相鄰點參數變化率。ξi+1,i的表達式如下:

設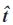
對方程(17)中的變量s求微分,可得單位切向量:

3 數值算例與分析
理論上可以在一些典型物體(如圓柱體、錐體)上計算爬行射線,因此,可以從這些對象的分析結果中驗證所提出的方法是否有效。
3.1 圓柱體
圖9所示為圓柱表面(均勻網格)爬行波射線傳播軌跡圖。圓柱的半徑為1 m,高為3 m。表1為爬行波尋跡結果,起始點為(1,0,0)。

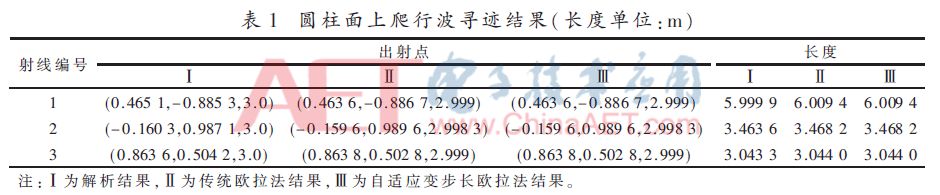
從表1可知,采用自適應變步長歐拉法得到的數值結果與解析方法的結果吻合得非常好,由此可證明該尋跡算法正確性。
3.2 任意曲面目標
圖10所示為任意曲面表面(非均勻網格表面)爬行波射線傳播軌跡圖。根據微分幾何知識,球面上的數值結果可以直接由理論值得到驗證。表2為爬行波尋跡結果,起始點為(1.0,0.0,0.0)。
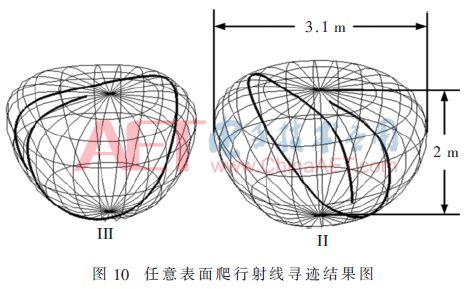
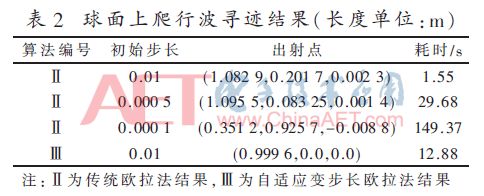
如圖10所示,提出的方法結果與理論結果吻合較好。從表2和圖10可以看出,盡管隨著離散步長的增加歐拉方法的誤差減少了,但是耗時也增加了很多。更重要的是,如果離散步長繼續增加下去,結果完全錯誤,這意味著歐拉方法不穩定。
4 結論
對于任意形狀NURBS目標表面爬行波射線軌跡尋跡,本文提出了基于自適應變步長歐拉法的快速有效的尋跡算法。為了驗證該尋跡算法的正確性與有效性,給出了幾個典型驗證算例。相比于傳統的歐拉法,自適應變步長歐拉法不僅繼承了傳統歐拉法的效率高的優勢,而且該算法適用于任意的光滑曲面。
-
算法
+關注
關注
23文章
4600瀏覽量
92647 -
高頻電磁
+關注
關注
0文章
3瀏覽量
5246 -
尋跡算法
+關注
關注
1文章
2瀏覽量
3538
原文標題:【學術論文】基于自適應變步長歐拉法的NURBS曲面爬行波尋跡算法
文章出處:【微信號:ChinaAET,微信公眾號:電子技術應用ChinaAET】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦

郭天祥 mini 80E升級版的蜂鳴器怎么不響呢??
上海升級版超級電容公交車投運
[推薦] (不看后悔)Android開發資料分享- 免積分(升級版)
HFSS高頻電磁場仿真應用
STM32電磁尋跡、紅外尋跡,遙控小車制作教程
電磁爐電源芯片SM7028升級版SM7028B
DIY ARDUINO PRO MINI 2.0(升級版)





 基于高頻電磁的尋跡算法升級版介紹
基于高頻電磁的尋跡算法升級版介紹










評論