Philadelphia Media Network資深數據分析師Daniel McNichol使用R語言演示了畢達哥拉斯平均數在不同概率分布上的效果。
這篇則將在技術方面更深入一點,在一些概率分布合成的數據上探索這些平均數。接著我們將考察一些可供比較的“真實世界”大型數據集。這篇的使用的表述也會更簡短,假定讀者對高等數學和概率論有所了解。
畢達哥拉斯平均數溫習
讓我們復習一下,有3種畢達哥拉斯平均數,遵循如下不等關系:
調和平均數 ≤ 幾何平均數 ≤ 算術平均數
僅當數據集中的所有數字都相等時,這3種平均數才相等。
算術平均數通過加法和除法得到。
幾何平均數通過乘法和開方根得到。
調和平均數通過倒數、加法、除法得到。
它們的公式為:
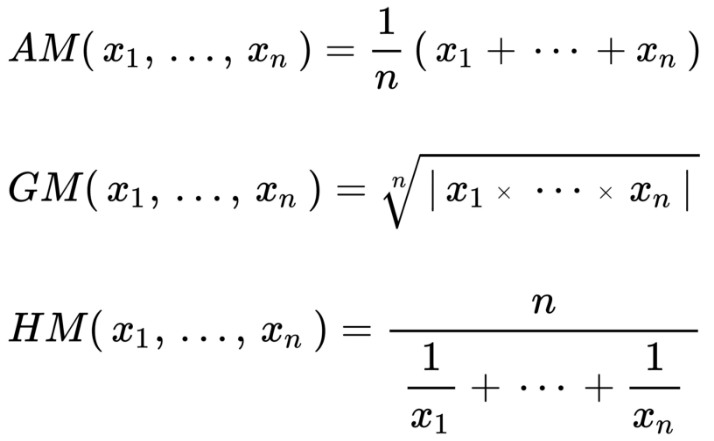
圖片來源:維基百科
每種平均數可以表達為另一種平均數的再配置。例如:
幾何平均數不過是數據集中的值的對數變換的算術平均數的反對數。有時它也能保留伸縮到同一分母后的算術平均數的次序。
調和平均數不過是數據集中的值的倒數的算術平均數的倒數。它也可以通過適當加權算術平均數重現。
經驗規則:
算術平均數最適合相加的、線性的、對稱的、正態/高斯數據集。
幾何平均數最適合相乘的、幾何的、指數的、對數正態分布的、扭曲的數據集,以及尺度不同的比率和復合增長的比率。
調和平均數是三種畢達哥拉斯平均數中最不常見的一種,但非常適合平均以分子為單位的比率,例如行程速度,一些財經指數,從物理到棒球的一些專門應用,還有評估機器學習模型。
限制:
由于相對不那么常用,幾何平均數和調和平均數對一般受眾而言可能難以理解甚至會誤導他們。
幾何平均數是無單位(unitless)的,尺度和可解釋的單位在相乘操作中丟失了。
幾何平均數和調和平均數無法處理包含0的數據集。
詳細的討論,請參閱上篇。下面我們將查看一些實際的例子。
合成數據集
上篇中,我們在一些微不足道的數據集(等差數列和等比數列)上觀察了畢達哥拉斯平均數的效果。這里我們將查看一些更大的合成數據集(實數集上的多種概率分布)。
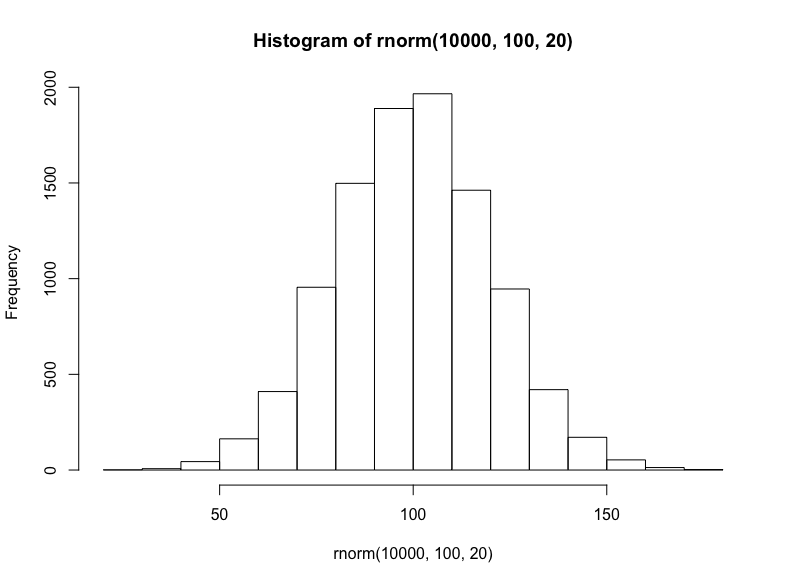
就相加或線性數據集而言,我們將從隨機正態分布(均值100、標準差20)中抽取10000個樣本:
hist(
rnorm( 10000, 100, 20 )
)
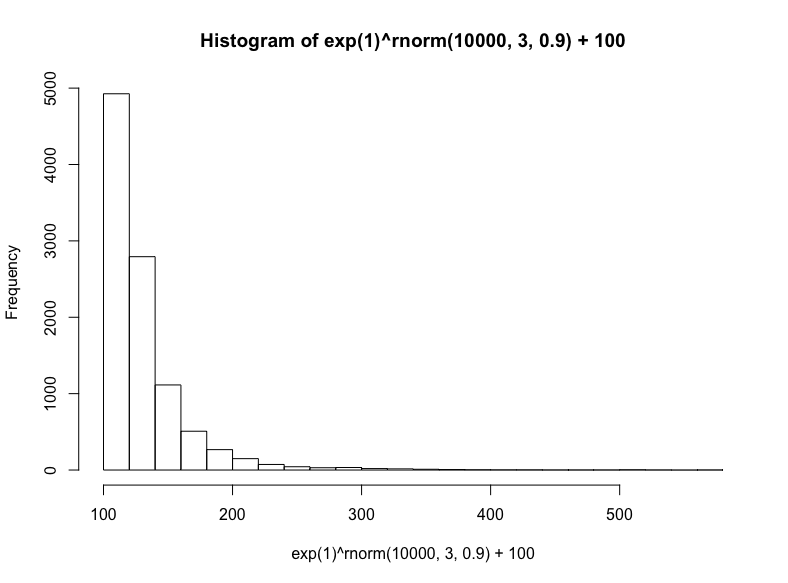
接著我們將模擬三種相乘數據集(盡管這些數據集具有有意義的差別,仍然常常難以區分):對數正態分布、指數分布、冪律分布。
有很多種生成對數正態分布的方法——基本上任何獨立同分布的隨機變量的乘法過程都將生成對數正態分布——這也正是它在真實世界中如此常見的原因,特別是在人類活動中。出于簡單性和可解釋性方面的考慮,我們將以歐拉數為底數,以從正態分布抽取的隨機數為指數,然后加上100(使取值范圍大致相當我們之前的正態分布):
hist(
exp(1)^rnorm(10000,3,.9) + 100,
breaks = 39
)
技術上說,這是指數分布的一個特例,但我們將通過R的rexp函數生成另一個指數分布,我們只需指定樣本數以及衰減率(同樣,我們在結果上加上100):
hist(
rexp(10000, 1/10) +100
)
最后,我們將從正態分布取樣底數,以歐拉數為指數,接著加上100,生成冪律分布:
(注意,這是對數正態方法的反向操作,在生成對數正態分布時,我們以歐拉數為底數,以正態分布取樣為指數)
hist(
rnorm(10000, 3, 1)^exp(1) + 100
)
接著我們將使用ggridges包以更好地繪制分布,我們也將同時加載tidyverse包,任何有教養的R用戶都這么干:
library(tidyverse)
library(ggridges)
dist1 <- rnorm(10000, 100, 20) %>%
tibble(x=., distribution = "normal")
dist2 <- ( exp(1)^rnorm(10000, 3, .9) + 100 ) %>%
tibble(x=., distribution = "lognormal")
dist3 <- ( rexp(10000, 1/10) + 100 ) %>%
tibble(x=., distribution = "exponential")
dist4 <- ( rnorm(10000,3,1)^exp(1) + 100 ) %>%
tibble(x=., distribution = "power law")
dists <- bind_rows(dist1, dist2, dist3, dist4)
dist_ord <- c("normal", "lognormal", "exponential", "power law")
dists <- dists %>%
mutate(distribution = fct_relevel(distribution, dist_ord))
ggplot(dists, aes(x = x, y = fct_rev(distribution), fill=..x..)) +
geom_density_ridges_gradient(quantiles = 2, scale=0.9,
color='white', show.legend = F) +
theme_minimal(base_size = 13, base_family = "sans") +
scale_y_discrete(expand = c(0.1, 0)) + xlim(0, 250) +
theme(panel.grid.major = element_line(colour = "white",
size = .3),
panel.grid.minor = element_blank(),
plot.background = element_rect(fill = "whitesmoke"),
axis.title = element_blank(), legend.position="none") +
ggtitle(label = "Distributions")
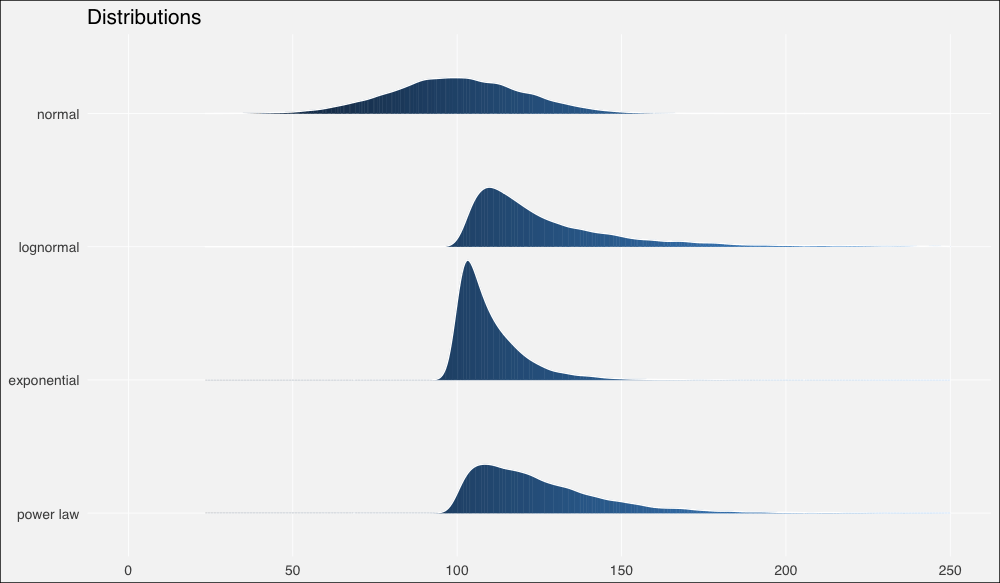
現在讓我們計算一些概述統計量。
由于R沒有內置幾何平均數或調和平均數的函數,我們需要自行定義:
# 幾何平均數函數
gm_mean = function(x, na.rm=TRUE){
exp(sum(log(x[x > 0]), na.rm=na.rm) / length(x))
}
dist_stats <- dists %>% group_by(distribution) %>%
summarise(median = median(x),
am = mean(x),
gm = gm_mean(x),
hm = 1/mean(1/x) # 調和平均數公式
)
輸出:
# A tibble: 4 x 5
distribution median am gm hm
1 normal 99.699.997.795.4
2 lognormal 120 129 127 125
3 exponential 107 110 110 109
4 power law 120 125 124 122
……在繪制的圖形上加上這些平均數:
ggplot(dists, aes(x = x, y = fct_rev(distribution), fill=..x..)) +
geom_density_ridges_gradient(quantiles = 2, scale=0.9,
color='white', show.legend = F) +
theme_minimal(base_size = 13, base_family = "sans") +
scale_y_discrete(expand = c(0.1, 0)) + xlim(0, 200) +
geom_point(data = dist_stats, aes(y=distribution, x=am),
colour="green3", shape=3, size=1, stroke =2,
alpha=.9, show.legend = F) +
geom_point(data = dist_stats, aes(y=distribution, x=gm),
colour="green3", fill="green3", shape=24, size=3,
alpha=.9, show.legend = F) +
geom_point(data = dist_stats, aes(y=distribution, x=hm),
colour="green3",fill= "green3", shape=25, size=3,
alpha=.9, show.legend = F) +
geom_segment(data = dist_stats, aes(x = median, xend = median,
y = c(4,3,2,1),
yend = c(4,3,2,1) + .3),
color = "salmon", show.legend = F) +
theme(panel.grid.major = element_line(colour = "white",
size = .3),
panel.grid.minor = element_blank(),
plot.background = element_rect(fill = "whitesmoke"),
axis.title = element_blank(), legend.position="none") +
ggtitle(label = "Distributions & summary statistics",
subtitle = "| : median : harmonic mean : geometric mean : arithmetic mean")
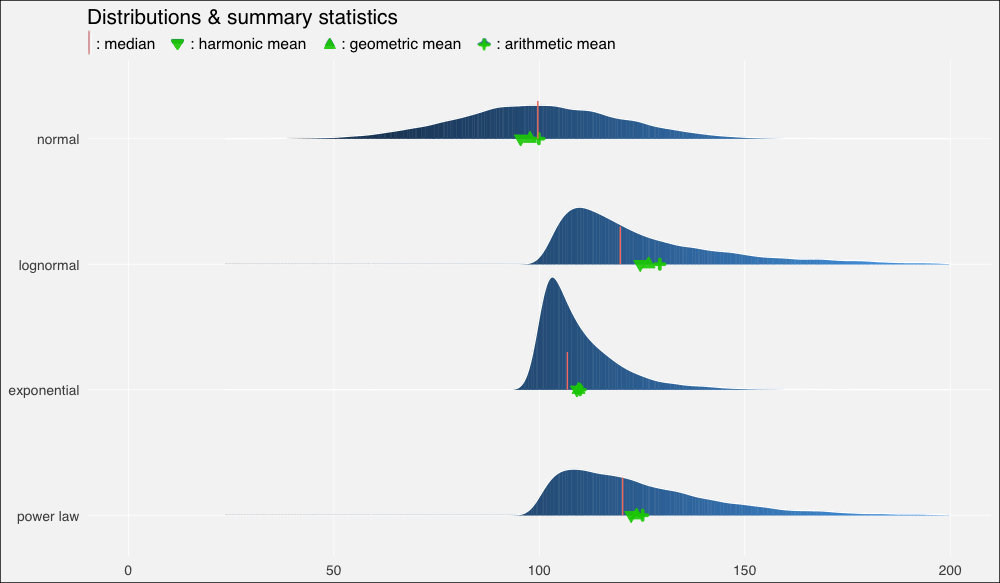
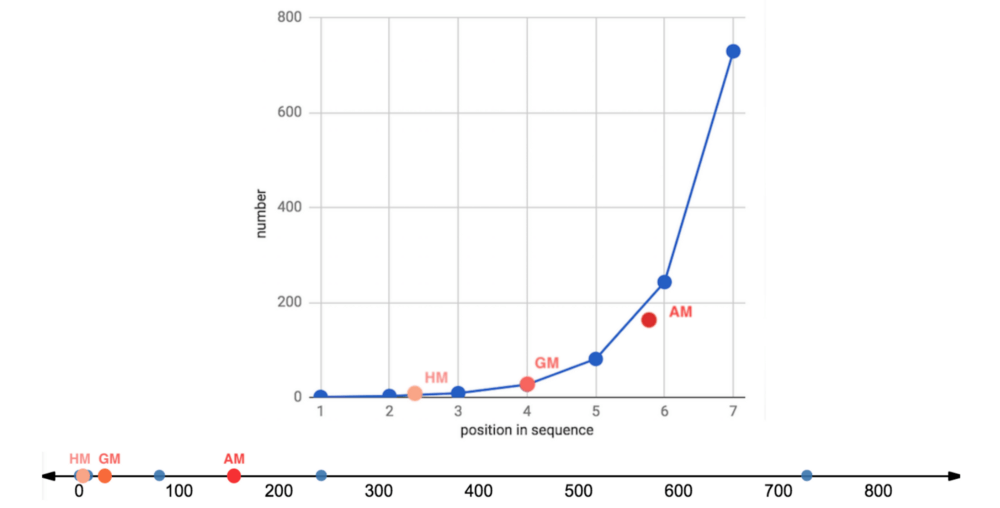
我們立刻看到了扭曲的密度的影響,以及平均數的重尾分布以及它們和中位數的關系:
在正態分布上,由于數據分布基本上是對稱的,中位數和算術平均數幾乎相等(分別是99.6和99.9)。
在向右扭曲的其他分布上,所有平均數均位于中位數右方,靠近數據集較密集的駝峰。
不過上圖中的平均數有點擁擠,所以讓我們放大一點來看(調整xlim()):
...xlim(90, 150)...
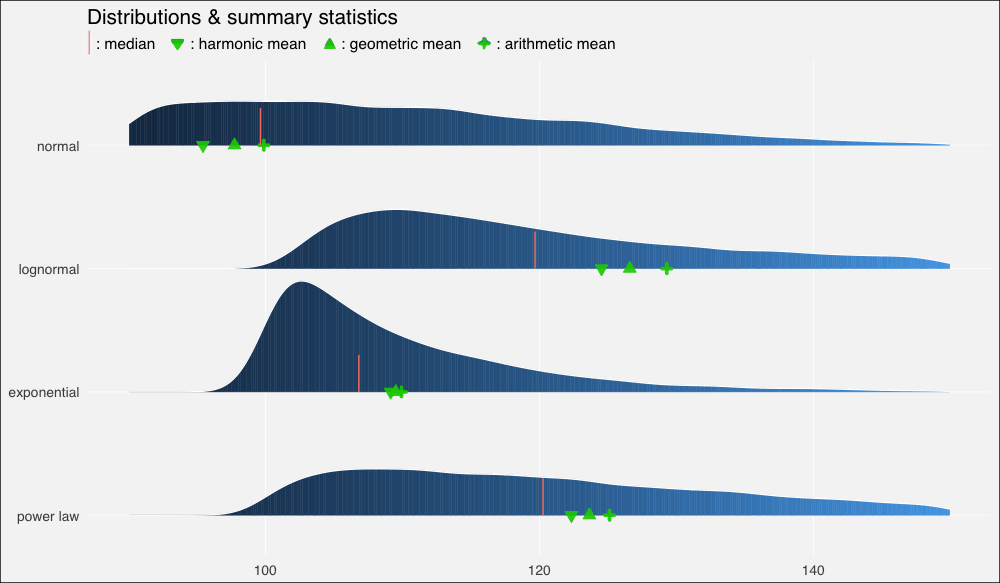
我們再一次看到,在正態、對稱數據集上,幾何平均數和調和平均數低估了數據的“中點”,不過三個平均數大致上間隔的空間是相等的。
在對數正態分布上,中等瘦削的長尾使平均數遠離中位數,甚至也扭曲了平均數的分布,使算術平均數到幾何平均數的距離比幾何平均數到調和平均數的距離更遠。
在指數分布上,數值高度密集,指數瘦削的短尾飛速衰減,使得平均數也擠作一團——盡管嚴重的扭曲仍然使它們偏離中位數。
冪律分布衰減較慢,也因此具有最肥的尾部。它的“主體”部分仍然是接近正態的,在不對稱分布中的扭曲是最輕微的。平均數之間的距離大致相等,不過仍然遠離中位數。
我之前提到過幾何平均數和算術平均數之間的對數關系:
幾何平均數不過是數據集中的值的對數變換的算術平均數的反對數。
為了驗證這一點,讓我們再看一看我們的概述統計量表格:
# A tibble: 4 x 5
distribution median am gm hm
1 normal 99.699.997.795.4
2 lognormal 120 129 127 125
3 exponential 107 110 110 109
4 power law 120 125 124 122
注意我們的對數正態分布的幾何平均數是127.
現在我們計算對數變換值的算術平均數:
dist2$x %>% log() %>% mean()
輸出:
4.84606
取反對數:
exp(1)^4.84606
輸出:
127.2381
現在,為了把這一點講透徹,讓我們看看為什么會這樣(以及對數正態是如何得名的):
減去我們原本加上的100,然后取對數:
(dist2$x — 100) %>% log() %>% hist()
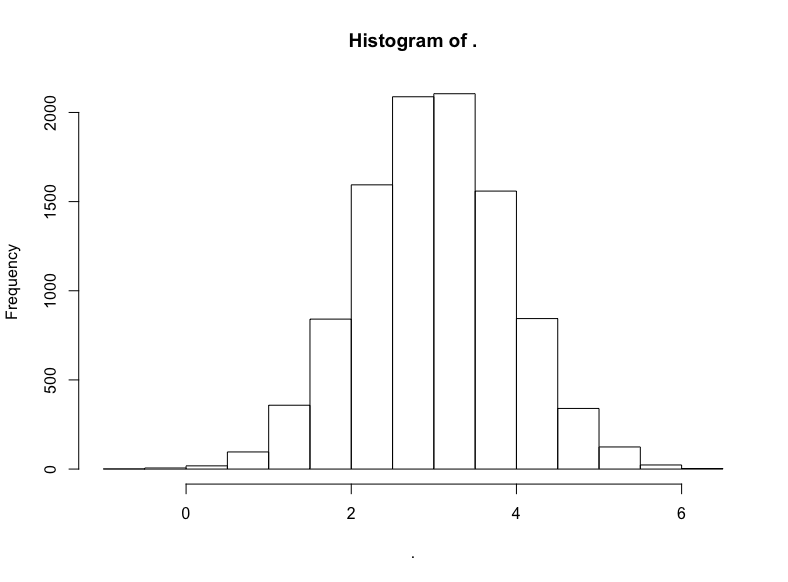
名副其實,對數正態分布的對數變換將產生正態分布。因此,正態分布中以相加為基礎的算術平均數的結果與對數正態分布中以相乘為本質的幾何平均數的結果是一致的。
我們不應該對對數正態分布的數據集經過對數變換得到的無可挑剔的正態分布過于印象深刻,畢竟我們在指定生成對數正態分布值的具體數據生成過程時就使用了正態分布,我們現在不過是反向操作以重現底層的正態分布而已。
現實世界中的事情很少如此整潔,現實世界的生成過程通常更復雜,是未知的,或者不可知的。因此如何建模和描述得自經驗的數據集充滿了困惑和爭議。
讓我們查看一些這樣的數據集,了解下真實世界的煩惱。
真實世界數據
盡管通常不像模擬數據那樣溫順,真實世界數據集通常至少再現了上述四種分布中的一種。
正態分布——喧鬧的“鐘形曲線”——最常出現在自然、生物場景中。身高和體重是經典的例子。因此,我們的第一直覺是看看可信賴的iris數據集。它確實滿足要求,但樣本數有點小(數據集中單種花卉的樣本數為50)。我想要更大的數據集。
所以讓我們加載bigrquery包:
library(bigrquery)
Google的BigQuery提供了眾多真實數據的公開數據集,其中一些非常大,例如基因、專利、維基百科文章數據。
回到我們最初的目標,natality(譯者注:natality意為出生率)看起來就很生物:
project <- “YOUR-PROJECT-ID”
sql <- “SELECT COUNT(*)
FROM `bigquery-public-data.samples.natality`”
query_exec(sql, project = project, use_legacy_sql = F)
(提示:由于有海量數據,因此你可能需要為訪問數據付費,不過每個月前1TB的數據訪問是免費的。另外,盡管出于明顯的原因,強烈不推薦使用SELECT *,SELECT COUNT(*)卻是一項免費的操作,使用它確定范圍是個好主意。)
輸出:
137826763
一億三千七百萬嬰兒數據!我們用不了這么多,所以讓我們隨機取樣1%嬰兒的體重,獲取前一百萬結果:
sql <- “SELECT weight_pounds
FROM `bigquery-public-data.samples.natality`
WHERE RAND() < .01”
natal <- query_exec(sql, project = project, use_legacy_sql = F,
max_pages = 100)
hist(natal$weight_pounds)生成:
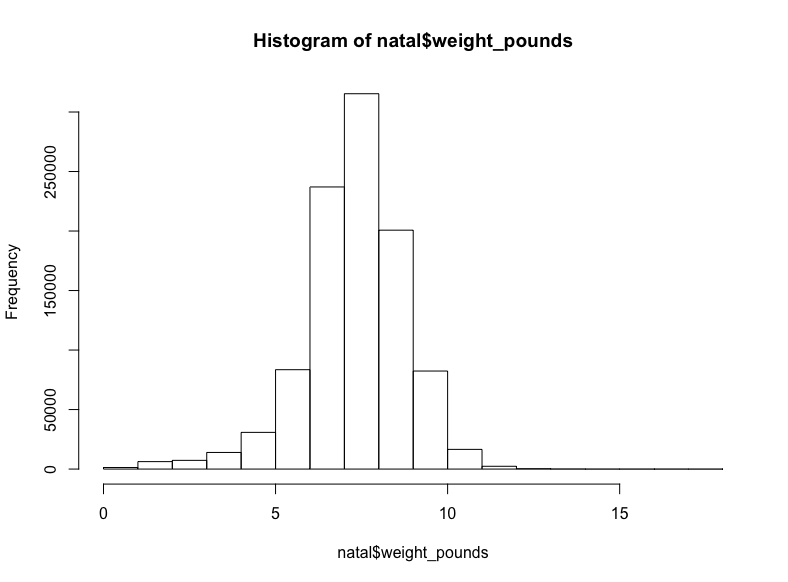
至少在我看來這是正態分布。
現在讓我們找找有些扭曲的相乘數據,讓我們從生物學轉向社會學。
我們將查看New York(紐約)數據集,其中包含各種城市信息,包括黃色出租車和綠色出租車的行程信息(譯者注:紐約的出租車分為黃、綠兩種,兩者允許接客區域不同)。
sql <- “SELECT COUNT(*)
FROM `nyc-tlc.green.trips_2015`”
query_exec(sql, project = project, use_legacy_sql = F)
輸出:
9896012
不到一千萬條記錄,所以讓我們抓取所有的行程距離:
(這可能需要花費一點時間)
sql <- "SELECT trip_distance FROM `nyc-tlc.green.trips_2015`"
trips <- query_exec(sql, project = project, use_legacy_sql = F)
hist(trips$trips_distance)
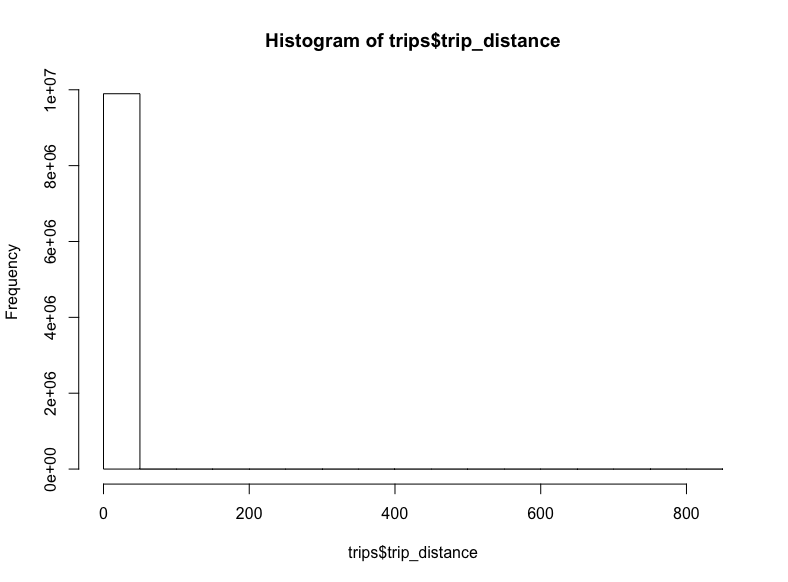
-_-
看起來一些極端的離散值將我們的x軸拉到了八百英里開外。對出租車而言,這也太遠了。讓我們移除這些離散值,將距離限定至20英里:
trips$trip_distance %>% subset(. <= 20) %>% hist()
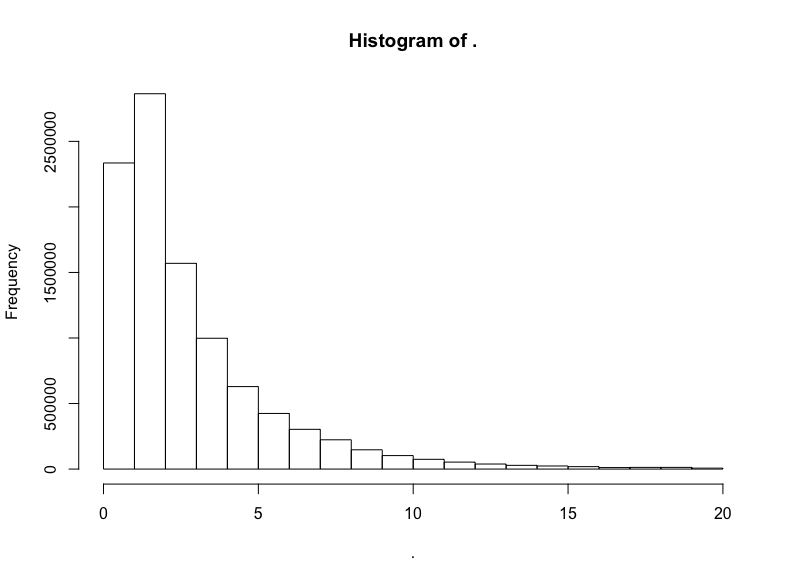
我們做到了,得到了對數正態分布標志性的長尾。讓我們驗證一下分布的對數正態性,繪制對數的直方圖:
trips$trip_distance %>% subset(. <= 20) %>% log() %>% hist()
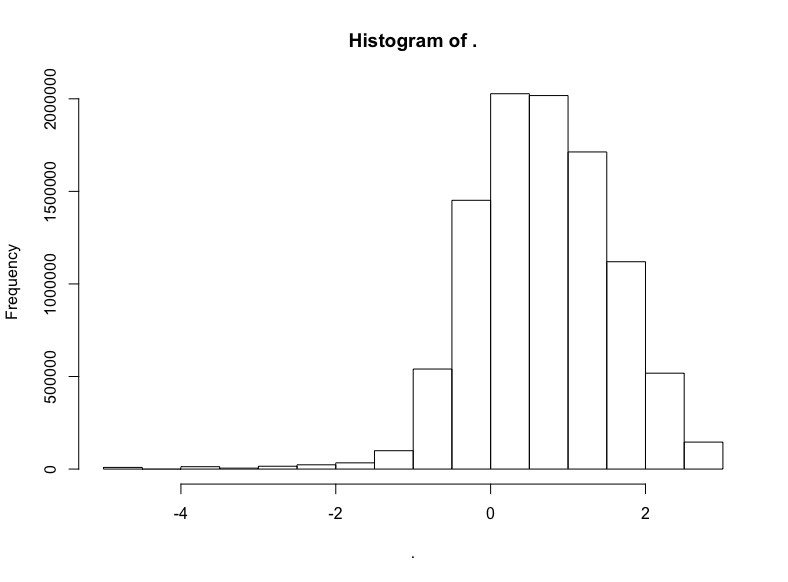
明顯有正態分布的樣子,不過偏離了一點靶心,有一點向左扭曲。哎呀,真實世界就是這樣的。不過我們有把握說,應用對數正態分布至少不算荒謬。
讓我們繼續前行。尋找更重尾分布的數據。這次我們將使用Github數據集:
sql <- "SELECT COUNT(*)
FROM `bigquery-public-data.samples.github_nested`"
query_exec(sql, project = project, use_legacy_sql = F)
輸出:
2541639
二百五十萬項記錄。我開始為本地機器的內存擔心了,所以我將通過隨機取樣去掉一半數據,然后查看剩余代碼倉庫的關注數(watchers):
sql <- “SELECT repository.watchers
FROM `bigquery-public-data.samples.github_nested`
WHERE RAND() < .5”
github <- query_exec(sql, project = project, use_legacy_sql = F,
max_pages = 100)
github$watchers %>% hist()
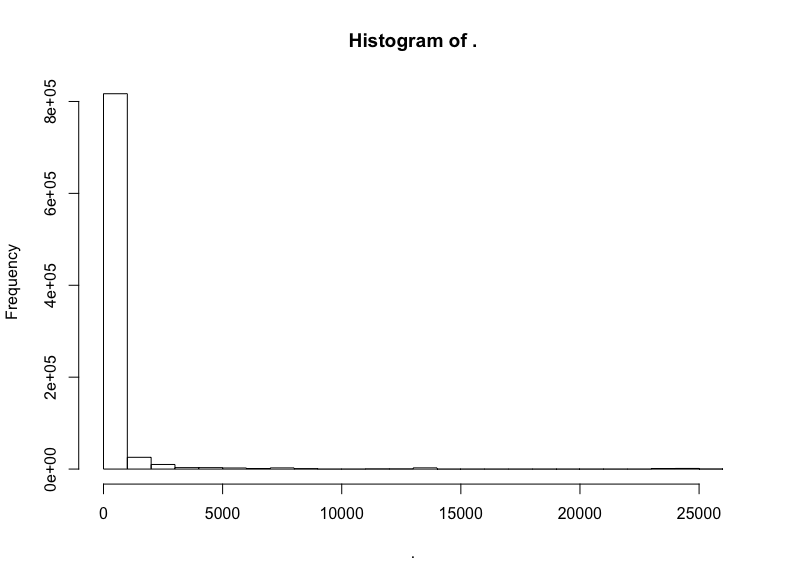
極端的長尾,所以讓我們移除過低和過高的關注數:
github$watchers %>% subset(5 < . & . < 3000) %>% hist()
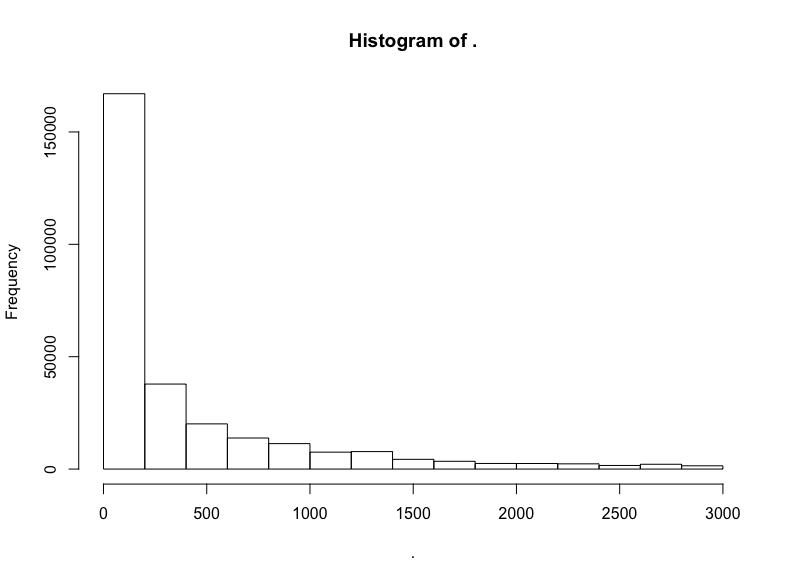
這是指數分布。
但是它是不是同時也是對數正態分布?
github$watchers %>% subset(5 < . & . < 3000) %>% log() %>% hist()
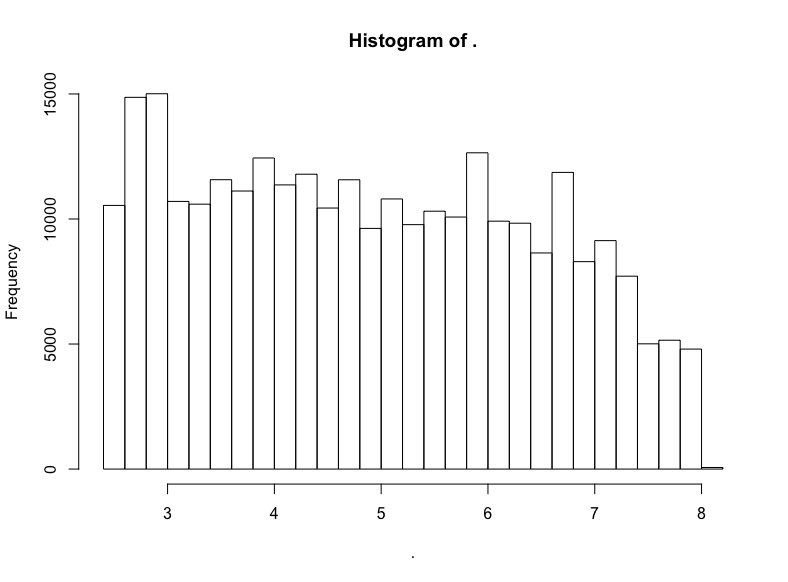
否。
不過我們看到了一頭珍稀的野獸:(逼近)LogUniform分布!
讓我們再從大數據中抽取一次,這次我們將查看Hacker News帖子的評分:
sql <- “SELECT COUNT(*)
FROM `bigquery-public-data.hacker_news.full`”
query_exec(sql, project = project, use_legacy_sql = F)
輸出:
16489224
我們抽取前10%的樣本:
sql <- “SELECT score
FROM `bigquery-public-data.hacker_news.full`
WHERE RAND() < .1”
hn <- query_exec(sql, project = project, use_legacy_sql = F,
max_pages = 100)
hn$score %>% hist()
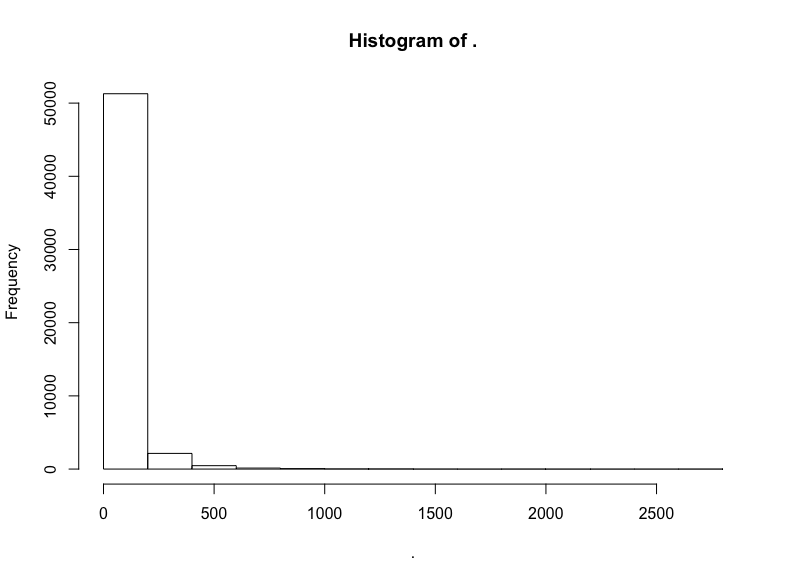
同樣,我們截取中間部分的評分:
hn$score %>% subset(10 < . & . <= 300) %>% hist()
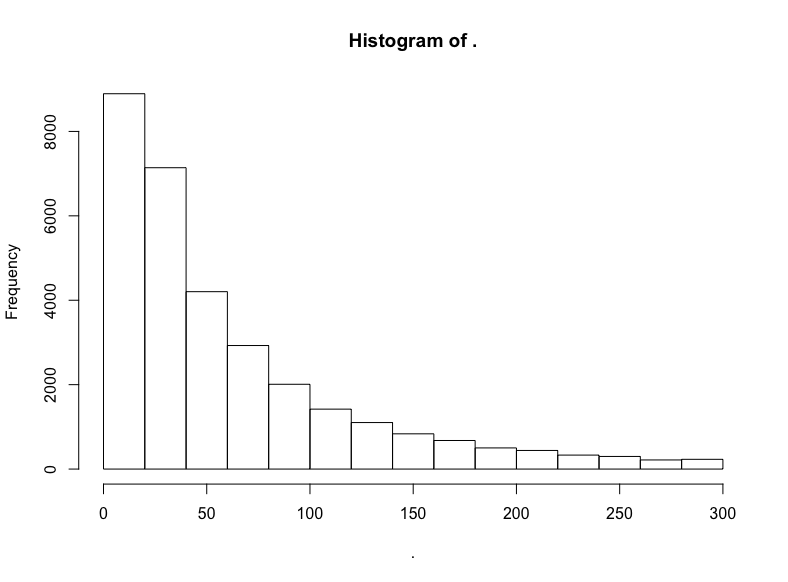
截取中間部分后,衰減得慢了。看看對數變換的結果?
hn$score %>% subset(10 < . & . <= 300) %>% log() %>% hist()
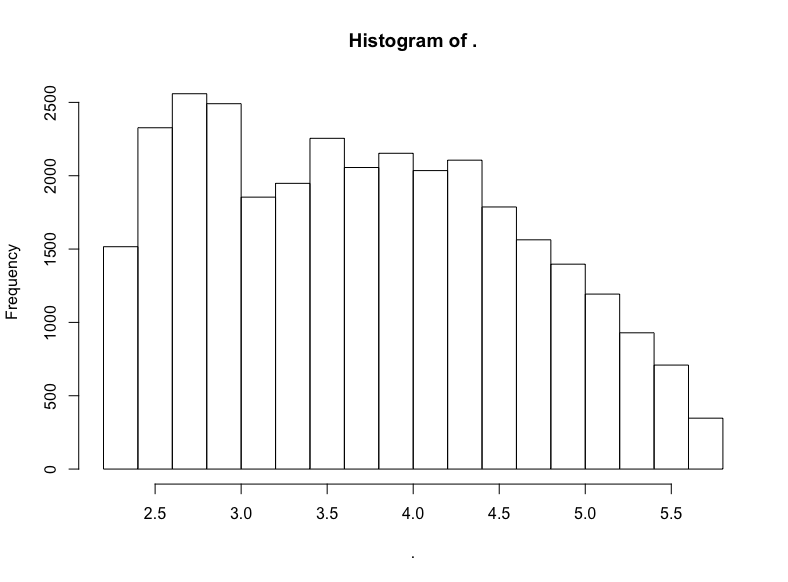
同樣大致是右向衰減的LogUniform分布。
我對冪律分布的搜尋沒有得到結果,這也許并不值得驚訝,畢竟冪律分布最常出現在網絡科學中(甚至,即使在網絡科學中,冪律分布看起來也比最初宣稱的要罕見)。
不管怎么說,讓我們也像模擬分布那樣繪制真實數據集的分布圖,并加以對比。同樣,我們將對其加以標準化,使其位于100左右。
# 定制標準化函數
normalize = function(x, na.rm = T){
(x-min(x[!is.na(x)]))/(max(x[!is.na(x)])-min(x[!is.na(x)]))
}
rndist1 <- (normalize(natality$weight_pounds) + 100) %>%
tibble(x=., distribution = "natal weights")
trip_trim <- trips$trip_distance %>% subset(. <= 20)
rndist2 <- (normalize(trip_trim) + 100) %>%
tibble(x=., distribution = "nyc green cab trips")
git_trim <- github$watchers %>% subset(5 < . & . < 3000)
rndist3 <- (normalize(git_trim) + 100) %>%
tibble(x=., distribution = "github watchers")
hn_trim <- hn$score %>% subset(10 < . & . <= 300)
rndist4 <- (normalize(hn_trim) + 100) %>%
tibble(x=., distribution = "hacker news scores")
rndists <- bind_rows(rndist1, rndist2, rndist3, rndist4)
rndist_ord <- c("natal weights", "nyc green cab trips",
"github watchers", "hacker news scores")
rndists <- rndists %>%
mutate(distribution = fct_relevel(distribution, rndist_ord))
ggplot(rndists, aes(x = x, y = fct_rev(distribution), fill=..x..)) +
geom_density_ridges_gradient(quantiles = 2, scale=0.9,
color='white', show.legend = F) +
theme_minimal(base_size = 13, base_family = "sans") +
scale_y_discrete(expand = c(0.1, 0)) + xlim(99.5, 101) +
theme(panel.grid.major = element_line(colour = "white", size = .3),
panel.grid.minor = element_blank(),
plot.background = element_rect(fill = "whitesmoke"),
axis.title = element_blank(), legend.position="none") +
ggtitle(label = "Distributions")
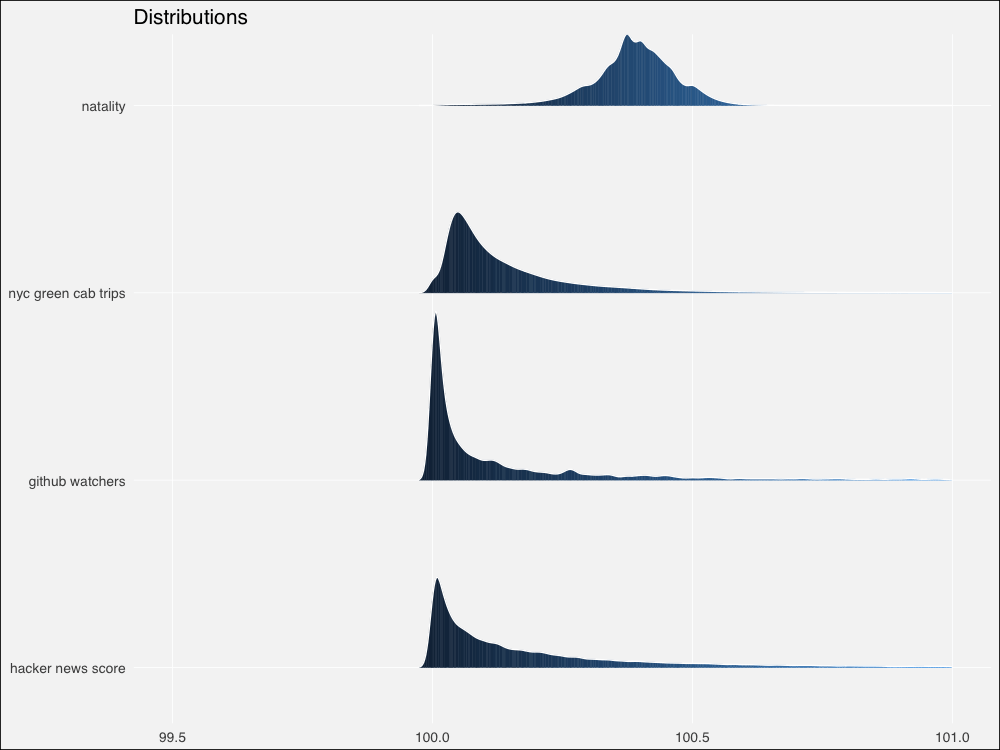
由于來自真實世界,和模擬分布相比,邊緣更加粗糙不平。不過仍然看起來相似。讓我們用Thomas Lin Pedersen的patchwork包繪制模擬分布和真實分布的對比圖:
# 將圖形分配給對象
p1 <-ggplot(dists, aes(x = x, y = fct_rev(distribution), fill=..x..)) +
geom_density_ridges_gradient(quantiles = 2, scale=0.9,
color='white', show.legend = F) +
theme_minimal(base_size = 13, base_family = "sans") +
scale_y_discrete(expand = c(0.1, 0)) + xlim(0, 250) +
theme(panel.grid.major = element_line(colour = "white", size = .3),
panel.grid.minor = element_blank(),
plot.background = element_rect(fill = "whitesmoke"),
axis.title = element_blank(), legend.position="none") +
ggtitle(label = "Distributions")
p2 <- ggplot(rndists, aes(x = x, y = fct_rev(distribution), fill=..x..)) +
geom_density_ridges_gradient(quantiles = 2, scale=0.9,
color='white', show.legend = F) +
theme_minimal(base_size = 13, base_family = "sans") +
scale_y_discrete(expand = c(0.1, 0)) + xlim(99.5, 101) +
theme(panel.grid.major = element_line(colour = "white", size = .3),
panel.grid.minor = element_blank(),
plot.background = element_rect(fill = "whitesmoke"),
axis.title = element_blank(), legend.position="none") +
ggtitle(label = "Distributions")
# 直接將圖形對象相加
p1 + p2
總體來看,模擬分布將為相鄰的真實數據集提供合理的模型,除了冪律 -> HackerNews評分這一對例外。
當然有很多模型擬合方面的嚴謹測試,不過讓我們直接在分布上繪制概述統計量,就像我們之前做的那樣。
不幸的是,標準化的真實世界數據扭曲了概述統計量計算,使得結果多多少少難以區分。我懷疑這可能是因為計算機的浮點計算精度問題(不過也可能只是因為我自己在數值計算上犯了錯誤)。我不得不使用未標準化的真實世界數據單獨繪制,然后嘗試手工對齊。
讓我們組合未標準化的分布,然后計算概述性數據:
# 未標準化
rdist1 <- natality$weight_pounds ?%>%
tibble(x=., distribution = "natal weights")
rdist2 <- trips$trip_distance %>% subset(. <= 20) %>%
tibble(x=., distribution = "nyc green cab trips")
rdist3 <- github$watchers %>% subset(5 < . & . < 3000) %>%
tibble(x=., distribution = "github watchers")
rdist4 <- hn$score %>% subset(10 < . & . <= 300) %>%
tibble(x=., distribution = "hacker news scores")
rdists <- bind_rows(rdist1, rdist2, rdist3, rdist4)
rdist_ord <- c("natal weights", "nyc green cab trips",
"github watchers", "hacker news scores")
rdists <- rdists %>%
mutate(distribution = fct_relevel(distribution, rdist_ord))
rdist_stats <- rdists %>% group_by(distribution) %>%
summarise(median = median(x, na, na.rm = T),
am = mean(x, na.rm = T),
gm = gm_mean2(x[x>0]),
hm = 1/mean(1/x[x>0], na.rm = T))
現在讓我們繪圖(這很丑陋因為我們需要為每個真實分布創建單獨的圖形,好在patchwork讓我們可以優雅地定義布局):
# 模擬分布的繪圖和之前一樣
pm1 <- ggplot(dists, aes(x = x, y = fct_rev(distribution), fill=..x..)) +
geom_density_ridges_gradient(quantiles = 2, scale=0.9,
color='white', show.legend = F) +
theme_minimal(base_size = 13, base_family = "sans") +
scale_y_discrete(expand = c(0.1, 0)) + xlim(0, 250) +
geom_point(data = dist_stats, aes(y=distribution, x=am),
colour="green3", shape=3, size=1, stroke =2,
alpha=.9, show.legend = F) +
geom_point(data = dist_stats, aes(y=distribution, x=gm),
colour="green3", fill="green3", shape=24, size=3,# stroke = 1,
alpha=.9, show.legend = F) +
geom_point(data = dist_stats, aes(y=distribution, x=hm),
colour="green3",fill= "green3", shape=25, size=3,# stroke = 1,
alpha=.9, show.legend = F) +
geom_segment(data = dist_stats, aes(x = median, xend = median,
y = c(4,3,2,1),
yend = c(4,3,2,1) + .3),
color = "salmon", show.legend = F)+
theme(panel.grid.major = element_line(colour = "white", size = .3),
panel.grid.minor = element_blank(),
plot.background = element_rect(fill = "whitesmoke"),
axis.title = element_blank(), legend.position="none") +
ggtitle(label = "Distributions & summary statistics",
subtitle = "| : median : harmonic mean : geometric mean : arithmetic mean")
# 真實數據
p3 <- ?ggplot(rdist1, aes(x = x, y = distribution, fill = ..x..)) +
geom_density_ridges_gradient(quantiles = 2, scale=0.9,
color='white', show.legend = F) +
theme_minimal(base_size = 13, base_family = "sans") +
scale_y_discrete(expand = c(0.1, 0)) + #xlim(3, 11) +
geom_point(data = rdist_stats[1,], aes(y=distribution, x=am),
colour="green3", shape=3, size=1, stroke =2,
alpha=.9, show.legend = F) +
geom_point(data = rdist_stats[1,], aes(y=distribution, x=gm),
colour="green3", fill="green3", shape=24, size=3,# stroke = 1,
alpha=.9, show.legend = F) +
geom_point(data = rdist_stats[1,], aes(y=distribution, x=hm),
colour="green3",fill= "green3", shape=25, size=3,# stroke = 1,
alpha=.9, show.legend = F) +
geom_segment(data = rdist_stats[1,], aes(x = median, xend = median,
y = 1,
yend = 1 + .3),
color = "salmon", show.legend = F)+
theme(panel.grid.major = element_line(colour = "white", size = .3),
panel.grid.minor = element_blank(),
plot.background = element_rect(fill = "whitesmoke"),
axis.title = element_blank(), legend.position="none",
axis.text.x=element_blank())
p4 <- ?ggplot(rdist2, aes(x = x, y = distribution, fill = ..x..)) +
geom_density_ridges_gradient(quantiles = 2, scale=0.9,
color='white', show.legend = F) +
theme_minimal(base_size = 13, base_family = "sans") +
scale_y_discrete(expand = c(0.1, 0)) + #xlim(-1, 4) +
geom_point(data = rdist_stats[2,], aes(y=distribution, x=am),
colour="green3", shape=3, size=1, stroke =2,
alpha=.9, show.legend = F) +
geom_point(data = rdist_stats[2,], aes(y=distribution, x=gm),
colour="green3", fill="green3", shape=24, size=3,# stroke = 1,
alpha=.9, show.legend = F) +
geom_point(data = rdist_stats[2,], aes(y=distribution, x=hm),
colour="green3",fill= "green3", shape=25, size=3,# stroke = 1,
alpha=.9, show.legend = F) +
geom_segment(data = rdist_stats[2,], aes(x = median, xend = median,
y = 1,
yend = 1 + .3),
color = "salmon", show.legend = F)+
theme(panel.grid.major = element_line(colour = "white", size = .3),
panel.grid.minor = element_blank(),
plot.background = element_rect(fill = "whitesmoke"),
axis.title = element_blank(), legend.position="none",
axis.text.x=element_blank())
p5 <- ?ggplot(rdist3, aes(x = x, y = distribution, fill = ..x..)) +
geom_density_ridges_gradient(quantiles = 2, scale=200,
color='white', show.legend = F) +
theme_minimal(base_size = 13, base_family = "sans") +
scale_y_discrete(expand = c(0.1, 0)) + #xlim(20, 450) +
geom_point(data = rdist_stats[3,], aes(y=distribution, x=am),
colour="green3", shape=3, size=1, stroke =2,
alpha=.9, show.legend = F) +
geom_point(data = rdist_stats[3,], aes(y=distribution, x=gm),
colour="green3", fill="green3", shape=24, size=3,# stroke = 1,
alpha=.9, show.legend = F) +
geom_point(data = rdist_stats[3,], aes(y=distribution, x=hm),
colour="green3",fill= "green3", shape=25, size=3,# stroke = 1,
alpha=.9, show.legend = F) +
geom_segment(data = rdist_stats[3,], aes(x = median, xend = median,
y = 1,
yend = 1 + .3),
color = "salmon", show.legend = F)+
theme(panel.grid.major = element_line(colour = "white", size = .3),
panel.grid.minor = element_blank(),
plot.background = element_rect(fill = "whitesmoke"),
axis.title = element_blank(), legend.position="none",
axis.text.x=element_blank())
p6 <- ?ggplot(rdist4, aes(x = x, y = distribution, fill = ..x..)) +
geom_density_ridges_gradient(quantiles = 2, scale=40,
color='white', show.legend = F) +
theme_minimal(base_size = 13, base_family = "sans") +
scale_y_discrete(expand = c(.01, 0)) + #xlim(0, 100) +
geom_point(data = rdist_stats[4,], aes(y=distribution, x=am),
colour="green3", shape=3, size=1, stroke =2,
alpha=.9, show.legend = F) +
geom_point(data = rdist_stats[4,], aes(y=distribution, x=gm),
colour="green3", fill="green3", shape=24, size=3,# stroke = 1,
alpha=.9, show.legend = F) +
geom_point(data = rdist_stats[4,], aes(y=distribution, x=hm),
colour="green3",fill= "green3", shape=25, size=3,# stroke = 1,
alpha=.9, show.legend = F) +
geom_segment(data = rdist_stats[4,], aes(x = median, xend = median,
y = 1,
yend = 1 + .3),
color = "salmon", show.legend = F)+
theme(panel.grid.major = element_line(colour = "white", size = .3),
panel.grid.minor = element_blank(),
plot.background = element_rect(fill = "whitesmoke"),
axis.title = element_blank(), legend.position="none")
# 魔法般的patchwork布局語法
pm1 | (p3 / p4 / p5 / p6)
有趣的是,我們的真實世界數據集的概述統計量看起來明顯比模擬分布上更為分散。讓我們放大一點看看。
為了節省篇幅,我這里不會重復粘貼代碼,基本上我不過是修改了pm1的xlim(90, 150),并且去掉了上述代碼中的xlim()行的注釋:
放大后對比更鮮明了。
我們對模擬和真實世界分布上的畢達哥拉斯平均數的探索到此為止。
如果你還沒有看過上篇,可以看一下,上篇給出了一個更明確、更直觀的介紹。同時,別忘了參考后面給出的鏈接和進一步閱讀。
另外,如果你想讀到更多這樣的文章,可以在Twitter、LinkedIn、Github上關注我(我在上面的用戶名都是dnlmc)。
-
概率
+關注
關注
0文章
17瀏覽量
13013 -
算術
+關注
關注
0文章
12瀏覽量
7370 -
數據集
+關注
關注
4文章
1205瀏覽量
24644
原文標題:平均而言,你用的是錯誤的平均數(下):平均數與概率分布
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
新手求助:請問怎么將數組中每100個數,求平均數
怎么查詢平均數
如何實現c++自動輸出平均數?
求無符號數的平均數
SV601187的詳細資料合集包括了電路圖,原理圖和介紹等詳細資料概述
CAN總線基礎的詳細資料概述
ADRF5144: 10 W平均數,硅SPDT,反射開關,1千赫至20千兆赫數據表 ADI





 概率分布合成的數據上平均數的探索詳細資料概述
概率分布合成的數據上平均數的探索詳細資料概述












評論