一、51%攻擊
51%攻擊指的是,有人掌握了全網一半以上的算力,就可以和全網其他算力進行對抗,更改區塊鏈記錄了。最根本的原因是比特幣區塊鏈采取的是最長鏈原則,即當前最長的鏈被認為是主鏈,是正確的鏈。51%具體能做什么呢?
1. 假設51%算力仍然是遵循比特幣的規則
這個時候,仍然需要簽名才能進行轉賬交易等,那么51%攻擊,不能修改別人的賬戶下的金額,不能將別人賬戶金額轉到自己的賬戶下,只能對自己的賬戶進行操作,比如雙重支付(雙重支付可以有兩種方式:要么是在交易被確認之前,要么攻擊者通過塊鏈分叉來完成)、阻止確認其他交易。
2. 假設51%算力不遵循比特幣的規則
這個時候,51%算力可以修改區塊鏈規則,比如,放棄非對稱加密的簽名機制,轉賬不需要簽名也可以進行,51%算力就可以將其他賬戶下的金額轉到自己名下,因為他掌握了一半以上的算力,所有規則都可以修改,不需要其他算力的參與(因為長遠來看,他總是能跑贏其他算力)。
二、6個確認數
為啥掌握51%的算力就能破壞比特幣網絡呢?從直觀感覺上確實如此,將攻擊節點算力和誠實節點算力當作兩個人,挖礦行為就像賽跑一樣,當然是速度快的人最終贏得比賽。其實中本聰在論文中做了數學上的分析。另外,現在比特幣轉賬,都建議等待6個確認數之后,資金才認為是安全的,在他的論文中也做了解釋。
首先,所有推導都有一個前提,就是區塊隨著時間按照大致恒定的速度產生,也就是說,每間隔T0(10分鐘)產生且只產生一個區塊。
假設當前網絡算力是H,誠實節點算力是pH,攻擊節點算力是qH,p + q = 1。因為算力本身就是指每個固定時間間隔內能計算Hash的次數,在比特幣中,每10分鐘產生一個區塊,我們可以將10分鐘當做一個最小的時間間隔,那么誠實節點算力和攻擊節點算力是說:每10分鐘發起一次計算的比賽,在這10分鐘內,誠實節點能計算k * p次,攻擊節點能計算k * q次(k只是一個系數而已,并不重要,重要的是比值),由前提可知:平均意義上,不存在誠實節點和攻擊節點都沒挖出區塊(某個10分鐘存在這個情況的話,那么下一個10分鐘會降低挖礦難度),也不存在誠實節點和攻擊節點都挖出區塊(某個10分鐘存在這個情況的話,那么下一個10分鐘會增加挖礦難度)。所以可以這樣認為:誠實節點有概率p挖出一個區塊(此時,攻擊節點沒有挖出區塊),攻擊節點有概率q挖出一個區塊(此時,誠實節點沒有挖出區塊)!即使誠實節點和攻擊節點在兩條分叉鏈上互不影響的挖礦,整個區塊鏈網絡也符合這個速度上的特點,這點是理解后面公式的關鍵。
關于某個交易得到多少個確認數之后資金才是安全的這個問題,在中本聰的論文中,將這個問題,分為兩步(假設是n個確認數之后):
1) n是指,在該交易之后,誠實節點已經挖出了n塊,也就是誠實節點對這個交易做了n次確認,因為攻擊節點的目的是破壞這個交易,不會浪費自己丁點兒的算力對這個交易做任何確認。這個時候,攻擊節點挖出了多少塊?(可以理解為,該交易之后,攻擊節點就在暗地里將區塊鏈條分叉了,并且不將自己分叉之后的工作放到區塊上,而是一直在自己的鏈條上單獨挖礦,等到合適的時機,才會公開自己的工作)
2) 假設這個時候,攻擊節點挖出了m塊,和誠實節點差距是z = n – m,攻擊節點彌補這個差距,追上誠實節點的可能性是多大?
先看第一個問題,中本聰從固定時間間隔的角度出發,他認為,誠實節點T0內挖出一個區塊的概率是p,那么平均而言,T0 / p 的時間間隔肯定能挖出一個區塊,那么誠實節點挖出n塊,共消耗了To * n / p的時間間隔。攻擊節點T0內挖出一個區塊的概率是q,那么T0 * n / p的時間間隔內,平均而言肯定能挖出q * n / p塊,而且每個T0 * n / p的時間間隔內,挖出的塊數差不多。將T0 * n / p當做一個單位時間間隔,那么求解的問題是:單位時間內隨機事件發生的次數的概率分布。而泊松分布就是描述這個概率的工具。可以參見:維基百科-泊松分布。λ 表示單位時間間隔內發生的次數,即為q * n / p。
而Analysis of hashrate-based double-spending這篇論文認為,不應該從固定時間間隔的角度進行估算,認為中本聰的計算只是一個簡化模型。該論文認為,依然從塊數出發,相當于:攻擊節點在經歷至少n次失敗(誠實節點挖出了n塊),能挖出的塊數,而負二項分布就是描述這個問題的工具,可以參見:維基百科-負二項分布。這個概率公式很簡單,不做解釋,可以參見論文。該論文最后得出的概率值,和中本聰的模型的概率值大致相當,只是略有差別。
接著看第二個問題,這里再次說一下推導的前提,就是區塊隨著時間按照大致恒定的速度產生,也就是說,每間隔T0(10分鐘)產生且只產生一個區塊。明確了這個前提,就能發現,其實誠實節點和攻擊節點是互斥的,每10分鐘只能有其中之一節點發現一個區塊,即使他們可能在兩個分叉上。那么這個問題就像中本聰在論文中說的,可以等同于賭徒破產問題,可以參見:維基百科-賭徒破產問題或者賭徒破產問題。其中的遞推公式
Pa= pPa+1+ q Pa-1,a=1,2,…,N-1
是說,假設初始有a個,如果以概率p獲得一個金幣,那么就等同于初始有a + 1個金幣,如果以概率q失去一個金幣,那么就等同于初始只有a – 1個金幣。應用到比特幣中,可以從誠實節點的角度出發,理解為,初始的時候,誠實節點有z個金幣,怎么賭博而失去了所有z個金幣或者財富一直增加。具體請參照中本聰的論文。
下面是Analysis of hashrate-based double-spending中列出的,不同攻擊節點q概率和等待確認數n的情況下,攻擊節點追趕上的概率(因為該論文提出的模型和中本聰提出的模型計算結果相差不大,并且提供的數據比較全,所以使用這個表格)
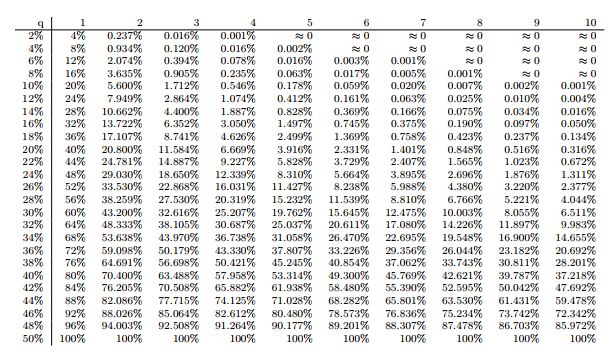
6個確認數是怎么得到的呢?是假設攻擊節點算力在10%左右,發起攻擊成功概率小于0.1%的確認數,從上表中可以看出是6。
-
區塊鏈
+關注
關注
110文章
15560瀏覽量
105787 -
比特幣
+關注
關注
57文章
7002瀏覽量
140339
原文標題:比特幣 (9):51%攻擊和6個確認數
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
尋找超導量子比特信息丟失的原因
科技看點:微軟將審議比特幣投資提案 2024年烏鎮峰會AI“含量”高
一種使用LED組成一個丘比特之箭圖案的設計
馬斯克:比特幣是有價值的
英偉達高端顯卡供不應求,國內或解除比特幣禁令
比特幣價格首次破7萬美元,看漲期權熱度不減
斯比特沖刺創業板上市
量子比特的“記憶力”——相干時間

比特與瓦特6精彩預告|“巨型充電寶”給紅海新城供電,主打一個“穩”!
低比特量化技術如何幫助LLM提升性能





 比特幣51%攻擊是什么?比特幣6個確認數是怎么得到的?
比特幣51%攻擊是什么?比特幣6個確認數是怎么得到的?










評論