編者按:無需艱深的數學,[24]7.ai首席數據科學家Abhishek Ghose帶你入門SVM(支持向量機)。
如果你曾經使用機器學習解決分類問題,你可能聽說過支持向量機(SVM)。五十年來,SVM隨著時間而演化,并在分類之外得到應用,例如回歸、離散值分析、排序。
SVM是許多機器學習從業者軍火庫中的最愛。在247.ai,我們同樣使用SVM解決各種各樣的問題。
本文將試圖從較高的層次講解SVM的機制。我將聚焦于發展直覺而不是嚴謹的細節。這意味著我們將跳過盡可能多的數學,發展對SVM工作原則的強有力的直覺。
分類問題
假設你的大學開設了一門機器學習(ML)課程。課程導師發現數學或統計學好的學生表現最佳。隨著時間的推移,積累了一些數據,包括參加課程的學生的數學成績和統計學成績,以及在ML課程上的表現(使用兩個標簽描述,“優”、“差”)。
現在,課程導師想要判定數學、統計學分數和ML課程表現之間的關系。也許,基于這一發現,可以指定參加課程的前提條件。
這一問題如何求解?讓我們從表示已有數據開始。我們可以繪制一張二維圖形,其中一根軸表示數學成績,另一根表示統計學成績。這樣每個學生就成了圖上的一個點。
點的顏色——綠或紅——表示學生在ML課程上的詞表現:“優”或“差”。

當一名學生申請加入課程時,會被要求提供數學成績和統計學成績。基于現有的數據,可以對學生在ML課程上的表現進行有根據的猜測。
基本上我們想要的是某種“算法”,接受“評分元組”(math_score, stats_score)輸入,預測學生在圖中是紅點還是綠點(綠/紅也稱為分類或標簽)。當然,這一算法某種程度上包括了已有數據中的模式,已有數據也稱為訓練數據。
在這個例子中,找到一條紅聚類和綠聚類之間的直線,然后判斷成績元組位于線的哪一邊,是一個好算法。

這里的直線是我們的分界(separating boundary)(因為它分離了標簽)或者分類器(classifier)(我們使用它分類數據點)。上圖顯示了兩種可能的分類器。
好 vs 差的分類器
這里有一個有趣的問題:上面的兩條線都分開了紅色聚類和綠色聚類。是否有很好的理由選擇一條,不選擇另一條呢?
別忘了,分類器的價值不在于它多么擅長分離訓練數據。我們最終想要用它分類未見數據點(稱為測試數據)。因此,我們想要選擇一條捕捉了訓練集中的通用模式(general pattern)的線,這樣的線在測試集上表現出色的幾率很大。
上面的第一條線看起來有點“歪斜”。下半部分看起來太接近紅聚類,而上半部分則過于接近綠聚類。是的,它完美地分割了訓練數據,但是如果它看到略微遠離其聚類的測試數據點,它很有可能會弄錯標簽。
第二條線沒有這個問題。
我們來看一個例子。下圖中兩個方形的測試數據點,兩條線分配了不同的標簽。顯然,第二條線的分類更合理。

第二條線在正確分割訓練數據的前提下,盡可能地同時遠離兩個聚類。保持在兩個聚類的正中間,讓第二條線的“風險”更小,為每個分類的數據分布留出了一些搖動的空間,因而能在測試集上取得更好的概括性。
SVM試圖找到第二條線。上面我們通過可視化方法挑選了更好的分類器,但我們需要更準確一點地定義其中的理念,以便在一般情形下加以應用。下面是一個簡化版本的SVM:
找到正確分類訓練數據的一組直線。
在找到的所有直線中,選擇那條離最接近的數據點距離最遠的直線。
距離最接近的數據點稱為支持向量(support vector)。支持向量定義的沿著分隔線的區域稱為間隔(margin)。
下圖顯示了之前的第二條線,以及相應的支持向量(黑邊數據點)和間隔(陰影區域)。

盡管上圖顯示的是直線和二維數據,SVM實際上適用于任何維度;在不同維度下,SVM尋找類似二維直線的東西。
例如,在三維情形下,SVM尋找一個平面(plane),而在更高維度下,SVM尋找一個超平面(hyperplane)——二維直線和三維平面在任意維度上的推廣。這也正是支持向量得名的由來。在高維下,數據點是多維向量,間隔的邊界也是超平面。支持向量位于間隔的邊緣,“支撐”起間隔邊界超平面。
可以被一條直線(更一般的,一個超平面)分割的數據稱為線性可分(linearly separable)數據。超平面起到線性分類器(linear classifier)的作用。
允許誤差
在上一節中,我們查看的是簡單的情形,完美的線性可分數據。然而,現實世界通常是亂糟糟的。你幾乎總是會碰到一些線性分類器無法正確分類的實例。
下圖就是一個例子。

顯然,如果我們使用一個線性分類器,我們將永遠不能完美地分割數據點。我們同樣不想干脆拋棄線性分類器,因為除了一些出軌數據點,線性分類器確實看起來很適合這個問題。
SVM允許我們通過參數C指定愿意接受多少誤差。C讓我們可以指定以下兩者的折衷:
較寬的間隔。
正確分類訓練數據。C值較高,意味著訓練數據上容許的誤差較少。
再重復一下,這是一個折衷。以間隔的寬度為代價得到訓練數據上更好的分類。
下圖展示了隨著C值的增加,分類器和間隔的變化(圖中沒有畫出支持向量):

上圖中,隨著C值的增加,分割線逐漸“翹起”。在高C值下,分割線試圖容納右下角大部分的紅點。這大概不是我們想要的結果。而C=0.01的圖像看起來更好的捕捉了一般的趨勢,盡管和高C值情形相比,他在訓練數據上的精確度較低。
同時,別忘了這是折衷,注意間隔是如何隨著C值的增加而收窄的。
在上一節的例子中,間隔曾經是數據點的“無人區”。正如我們所見,這里再也無法同時得到良好的分割邊界和相應的不包含數據點的間隔。總有一些數據點蔓延到了間隔地帶。
由于現實世界的數據幾乎從來都不是整潔的,因此決定較優的C值很重要。我們通常使用交叉驗證(cross-validation)之類的技術選定較優的C值。
非線性可分數據
我們已經看到,支持向量機有條不紊地處理完美線性可分或基本上線性可分的數據。但是,如果數據完全線性不可分,SVM的表現如何呢?畢竟,很多現實世界數據是線性不可分的。當然,尋找超平面沒法奏效了。這看起來可不妙,因為SVM很擅長找超平面。
下面是一個非線性可分數據的例子(這是知名的XOR數據集的一個變體),其中的斜線是SVM找到的線性分類器:

顯然這結果不能讓人滿意。我們需要做得更好。
注意,關鍵的地方來了!我們已經有了一項非常擅長尋找超平面的技術,但是我們的數據卻是非線性可分的。所以我們該怎么辦?將數據投影到一個線性可分的空間,然后在那個空間尋找超平面!
下面我們將逐步講解這一想法。
我們將上圖中的數據投影到一個三維空間:

下面是投影到三維空間的數據。你是不是看到了一個可以悄悄放入一個平面的地方?

讓我們在其上運行SVM:
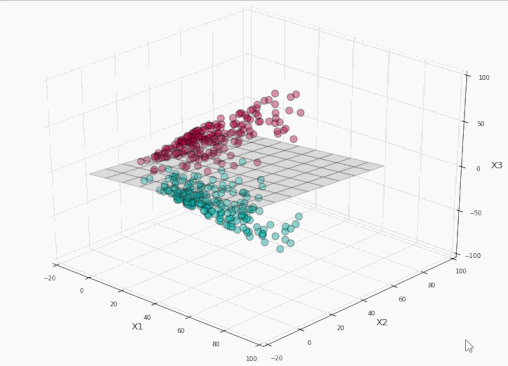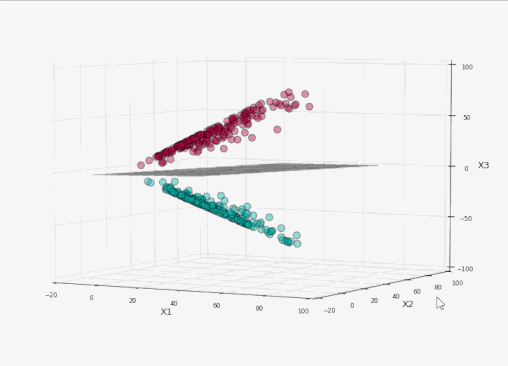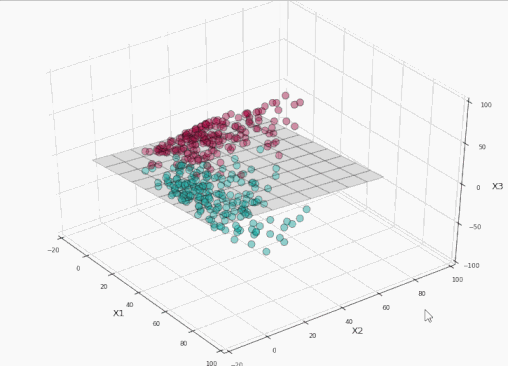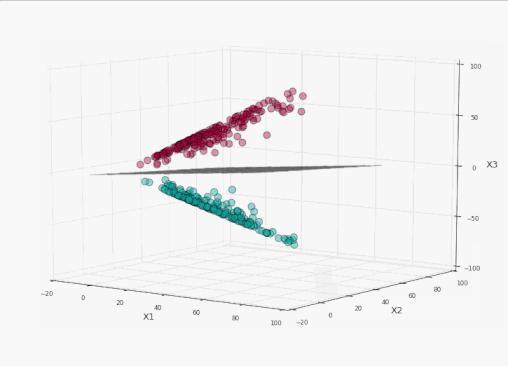
太棒了!我們完美地分割了標簽!現在讓我們將這個平面投影到原本的二維空間:

訓練集上精確度100%,同時沒有過于接近數據!耶!
原空間的分割邊界的形狀由投影決定。在投影空間中,分割邊界總是一個超平面。
別忘了,投影數據的主要目標是為了利用SVM尋找超平面的強大能力。
映射回原始空間后,分割邊界不再是線性的了。不過,我們關于線性分割、間隔、支持向量的直覺在投影空間仍然成立。

我們可以看到,在左側的投影空間中,三維的間隔是超平面之上的平面和之下的平面中間的區域(為了避免影響視覺效果,沒有加上陰影),總共有4個支持向量,分別位于標識間隔的上平面和下平面。
而在右側的原始空間中,分割邊界和間隔都不再是線性的了。支持向量仍然在間隔的邊緣,但單從原始空間的二維情形來看,支持向量好像缺了幾個。
現在讓我們回過頭去分析下發生了什么?
1. 如何知道應該把數據投影到哪個空間?
看起來我找了一個非常特定的解——其中甚至還有√2。
上面我是為了展示投影到高維空間是如何工作的,所以選擇了一個特定的投影。一般而言,很難找到這樣的特定投影。不過,感謝Cover定理,我們確實知道,投影到高維空間后,數據更可能線性可分。
在實踐中,我們將嘗試一些高維投影,看看能否奏效。實際上,我們可以將數據投影到無窮(infinite)維,通常而言效果很好。具體細節請看下一節。
2. 所以我首先投影數據接著運行SVM?
否。為了讓上面的例子易于理解,我首先投影了數據。其實你只需讓SVM為你投影數據。這帶來了一些優勢,包括SVM將使用一種稱為核(kernels)的東西進行投影,這相當迅速(我們很快將講解原因)。
另外,還記得我在上一點提過投影至無窮維么?那該如何表示、存儲無窮維呢?結果SVM在這一點上非常聰明,同樣,這和核有關。
現在是時候查看下核了。
核
這是讓SVM奏效的秘密武器。這里我們需要一點數學。
讓我們回顧下之前的內容:
SVM在線性可分的數據上效果極為出色。
使用正確的C值,SVM在基本線性可分的數據上效果相當出色。
線性不可分的數據可以投影至完美線性可分或基本線性可分的空間,從而將問題轉化為1或2.
看起來讓SVM得到普遍應用的關鍵是投影到高維。這正是核的用武之地。
SVM優化
之前我們略過了SVM尋找超平面的數學部分,現在為了更好地說明核的作用,我們需要還下之前的欠債。
假設訓練數據集包含n個數據點,其中每個數據點用一個元組表示(xi, yi),其中xi為表示數據點的向量,yi為數據點的分類/標簽(不妨令yi的取值為-1或1)。那么,分割超平面就可以表示為:
wx - b = 0
其中,w為超平面的法向量。
將某一數據點xi代入wx - b后,根據所得結果的正負,就可以判斷數據點的分類。
相應地,確定間隔的兩個超平面則可以表示為
wx - b = 1 wx - b = -1
這兩個超平面之間的距離,也就是間隔的寬度為2/||w||

SVM的目標是在正確分類的前提下,最大化間隔寬度,也就是說,在滿足yi(wxi- b) >= 1的前提下,最大化2/||w||,也就是最小化||w||。
上式中,i = 1, …, n,也就是說,所有數據點都要滿足。但實際上,并不需要為所有數據點進行計算,只需要為所有支持向量計算即可。另外,上式中,我們乘上了yi(取值為1或-1),這就同時保證了間隔兩側的數據點都符合要求。
下面我們需要使用一些更深入的數學。顯然,最小化||w||等價于最小化

這一變換表明這是一個二次優化問題,有成熟的方案可以使用。
不過,通過拉格朗日對偶(Lagrange Duality)變換,可以進一步將其轉換為對偶變量(dual variable)優化問題:

加入拉格朗日乘數
然后可以找出更高效的求解方法:(這里略去具體推導過程)

另外,在推導過程中,我們得到了一個中間結果,w可以通過下式計算:

你可以不用在意以上公式的細節,只需注意一點,以上計算都是基于向量的內積。也就是說,無論是超平面的選取,還是確定超平面后分類測試數據點,都只需要計算向量的內積。
核函數
而核函數(kernel function),簡稱核(kernel)正是算內積的!核函數接受原始空間中兩個數據點作為輸入,可以直接給出投影空間中的點積。
讓我們回顧下上一節的例子,看看相應的核函數。我們同時也將跟蹤投影和內積的運算量,以便和核函數對比。
給定數據點i:

相應的投影為:

算下得到投影需要的運算量:
計算第一維:1次乘法
計算第二維:1次乘法
計算第三維:2次乘法
共計1+1+2 =4次乘法
同理,數據點j投影也需要4次乘法。
數據點i和數據點j在投影空間的內積為:

內積計算需要3次乘法、2次加法。
也就是:
乘法:8(投影)+ 3(內積) = 11
加法:2(內積)
共計11 + 2 =13次運算
而以下核函數將給出相同結果:

以上核函數在原始空間計算內積,然后取平方,直接得到結果。
只需展開以上公式就可以驗證結果是一致的:

需要幾次運算?在二維情形下計算內積需要2次乘法、1次加法,然后平方又是1次乘法。所以總共是4次運算,僅僅是之前先投影后計算的運算量的31%。
看來用核函數計算所需內積要快得多。在這個例子中,這點提升可能不算什么:4次運算和13次運算。然而,如果數據點有許多維度,投影空間的維度更高,在大型數據集上,核函數節省的算力將飛速累積。這是核函數的巨大優勢。
大多數SVM庫內置了流行的核函數,比如多項式(Polynomial)、徑向基函數(Radial Basis Function,RBF)、Sigmoid。當我們不進行投影時(比如本文的第一個例子),我們直接在原始空間計算點積——我們把這叫做使用線性核(linear kernel)。
許多核函數提供了微調的選項,比如,多項式核函數:

讓你可以選擇c和d的值。在上面的三維投影問題中,我使用的就是c=0、d=2的多項式核函數。
不過我們還沒有說完核函數的酷炫之處呢!
還記得我之前提過投影至無窮維?你應該已經猜到了吧,這需要正確的核函數。只需找到正確的核函數,我們就可以計算所需內積,并不用真的投影輸入數據,也不用操心存儲無窮維度。
RBF核就常常用于特定的無窮維投影。我們這里就不介紹相關的數學了,如果你想深入數學,可以參考文章底部給出的資源。
你也許會納悶,我們如何能夠計算無窮維上的點積?如果你為此困惑,可以想想無窮級數求和。
我們已經回答了上一節提出的問題。總結一下:
我們通常并不定義數據的投影。相反,我們從現有的核中選取一個,加以微調,以找到最匹配數據的核函數。
我們當然可以定義自己的核,甚至自行投影。但許多情形下不必如此。至少,我們從嘗試現有核函數開始。
如果存在我們想要的投影的核,我們將使用它,因為核經常快很多。
RBF核可以投影數據點至無窮維。
SVM庫
你可以從以下SVM庫開始上手:
libSVM
SVM-Light
SVMTorch
scikit-learn之類的許多通用ML庫也提供了SVM模塊,這些模塊常常是專門SVM庫的封裝。我建議從久經考驗的libSVM開始。
libSVM可以作為命令行工具使用,也提供了Python、Java、Matlab封裝。只要你的數據文件的格式可以被libSVM理解(詳見README),你就可以開始使用了。
事實上,如果你需要快速了解不同核、C值等對尋找分割邊界的影響,你可以嘗試libSVM主頁上的“圖形界面”。標記數據點分類,選擇SVM參數,然后點擊運行(Run)!
這個可視化工具的魅力無可阻擋,下面是我標記的一些數據點:
沒錯,我要給SVM一點難度。
接著我嘗試了一些核:
這個可視化工具不顯示分割邊界,但會顯示SVM學習的屬于某一特定標簽的區域。如你所見,線性核完全忽略了紅點。它認為整個空間是黃色的(更準確地說,黃綠色)。而RBF核干凈利落地為紅點劃出了一個圈。
有幫助的資源
本文主要依靠可視化的直觀理解。雖然這是很棒的初步理解概念的方式,我仍然強烈建議你深入一點。畢竟有些地方可視化的直觀理解是不夠的。其中一些概念用于決定折衷優化,除非你查看數學,否則很難直觀地理解一些結果。
另外,數學也有助于理解核函數。例如,本文對RBF核的介紹一筆帶過。我希望它的“神秘”——和無窮維投影的關系,以及最后數據集上奇妙的結果(“圈”)——能讓你想要更深入地了解它。
推薦的資源
視頻講座:Learning from Data—— Yaser Abu-Mostafa的第14講至第16講討論了SVM以及核函數。如果你正在找ML的入門講座,我強烈推薦整個系列,它在數學性和直觀性上平衡得很好。
書籍:統計學習基礎—— Trevor Hastie、Robert Tibshirani、Jerome Friedman著。第4章介紹了SVM背后的基本想法,而第12章全面討論了SVM的細節。
快樂(機器)學習!
-
SVM
+關注
關注
0文章
154瀏覽量
32337 -
機器學習
+關注
關注
66文章
8306瀏覽量
131834
原文標題:SVM教程:支持向量機的直觀理解
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于MapReduce的SVM態勢評估算法
基于SVM-LeNet模型的行人檢測
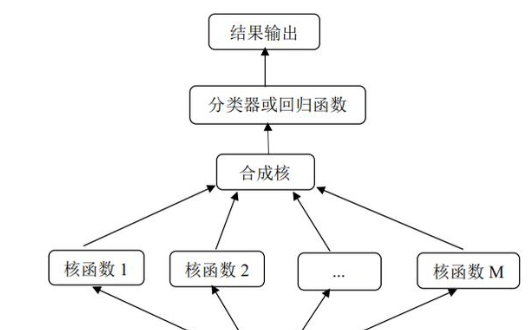
淺析SVM多核學習方法
一文帶你快速讀懂支持向量機 SVM 算法
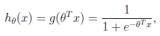




 帶你入門SVM,從較高的層次講解SVM的機制
帶你入門SVM,從較高的層次講解SVM的機制












評論