分三個部分來理解:
1.信號的角度
2.數學家的理解(外行)
3.與多項式的關系卷積這個東東是“信號與系統”中論述系統對輸入信號的響應而提出的。
因為是對模擬信號論述的,所以常常帶有繁瑣的算術推倒,很簡單的問題的本質常常就被一大堆公式淹沒了,那么卷積究竟物理意義怎么樣呢?
卷積表示為y(n) = x(n)*h(n)使用離散數列來理解卷積會更形象一點,我們把y(n)的序列表示成y(0),y(1),y(2) and so on; 這是系統響應出來的信號。同理,x(n)的對應時刻的序列為x(0),x(1),x(2)...and so on;其實我們如果沒有學過信號與系統,就常識來講,系統的響應不僅與當前時刻系統的輸入有關,也跟之前若干時刻的輸入有關,因為我們可以理解為這是之前時刻的輸 入信號經過一種過程(這種過程可以是遞減,削弱,或其他)對現在時刻系統輸出的影響,那么顯然,我們計算系統輸出時就必須考慮現在時刻的信號輸入的響應以 及之前若干時刻信號輸入的響應之“殘留”影響的一個疊加效果。假設0時刻系統的響應為y(0),若其在1時刻時,此種響應未改變,則1時 刻的響應就變成了y(0)+y(1),叫序列的累加和(與序列的和不一樣)。但常常系統中不是這樣的,因為0時刻的響應不太可能在1時刻仍舊未變化,那么 怎么表述這種變化呢,就通過h(t)這個響應函數與x(0)相乘來表述,表述為x(m)×h(n-m),具體表達式不用多管,只要記著有大概這種關系,引 入這個函數就能夠表述y(0)在1時刻究竟削弱了多少,然后削弱后的值才是y(0)在1時刻的真實值,再通過累加和運算,才得到真實的系統響應。再拓展點,某時刻的系統響應往往不一定是由當前時刻和前一時刻這兩個響應決定的,也可能是再加上前前時刻,前前前時刻,前前前前時刻,等等,那么怎么約束這 個范圍呢,就是通過對h(n)這個函數在表達式中變化后的h(n-m)中的m的范圍來約束的。即說白了,就是當前時刻的系統響應與多少個之前時刻的響應的 “殘留影響”有關。當考慮這些因素后,就可以描述成一個系統響應了,而這些因素通過一個表達式(卷積)即描述出來不得不說是數學的巧妙和迷人之處了。
++++++++++++++++++++++
卷積是人為定義的一種運算,就是為了計算的方便規定的一種算法。兩個函數普通乘積的積分變換(傅里葉變換與拉普拉斯變換)與這兩個函數積分變換的卷積建立了關系,使我們只要會求兩個函數的變換,利用卷積就可以求這兩個函數乘積的變換。卷積在數據處理中用來平滑,卷積有平滑效應和展寬效應.談起卷積分當然要先說說沖擊函數----這個倒立的小蝌蚪,卷積其實就是為它誕生的。“沖擊函數”是狄拉克為了解決一些瞬間作用的物理現象而提出的符號。古 人曰:“說一堆大道理不如舉一個好例子”,沖量這一物理現象很能說明“沖擊函數”。在t時間內對一物體作用F的力,我們可以讓作用時間t很小,作用力F很 大,但讓Ft的乘積不變,即沖量不變。于是在用t做橫坐標、F做縱坐標的坐標系中,就如同一個面積不變的長方形,底邊被擠的窄窄的,高度被擠的高高的,在數學中它可以被擠到無限高,但即使它無限瘦、無限高、但它仍然保持面積不變(它沒有被擠沒!),為了證實它的存在,可以對它進行積分,積分就是求面積嘛! 于是“卷積”這個數學怪物就這樣誕生了。說它是數學怪物是因為追求完美的數學家始終在頭腦中轉不過來彎,一個能瘦到無限小的家伙,竟能在積分中占有一席之 地,必須將這個細高挑清除數學界。但物理學家、工程師們確非常喜歡它,因為它解決了很多當時數學家解決不了的實際問題。最終追求完美的數學家終于想通了, 數學是來源于實際的,并最終服務于實際才是真。于是,他們為它量身定做了一套運作規律。于是,媽呀!你我都感覺眩暈的卷積分產生了。
目前,傅立葉變換最重要的應用之一就是可以將卷積方程變成兩個函數的乘積形式去求解。卷積分是積分方程家族的一名重要成員。
++++++++++++++++++++++
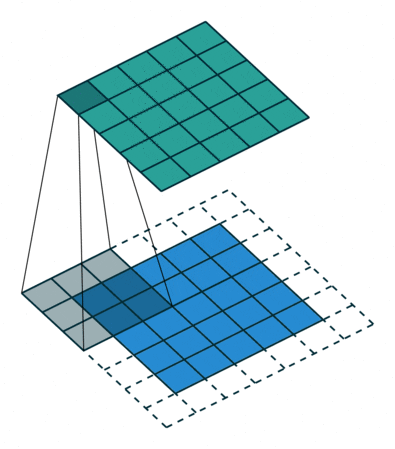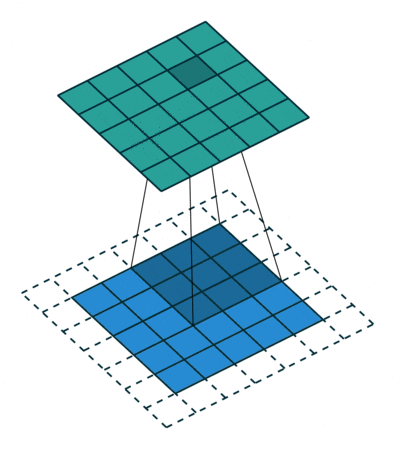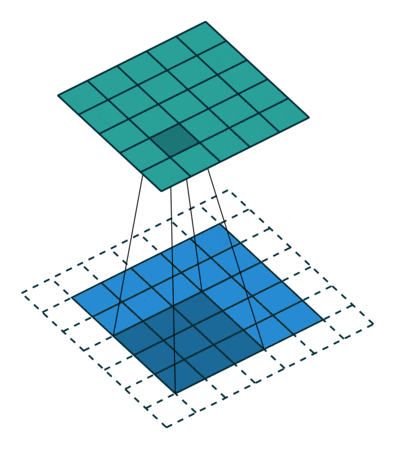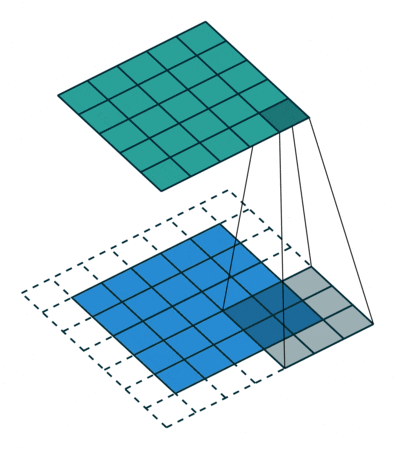
卷積是一種積分運算,它可以用來描述線性時不變系統的輸入和輸出的關系:即輸出可以通過輸入和一個表征系統特性的函數(沖激響應函數)進行卷積運算得到。 以下用$符號表示從負無窮大到正無窮大的積分。 一維卷積:y(t)=g(k)*x(k)=$g(k)x(t-k) 先把函數x(k)相對于原點反折,然后向右移動距離t,然后兩個函數相乘再積分,就得到了在t處的輸出。對每個t值重復上述過程,就得到了輸出曲線。 二維卷積:h(x,y)=f(u,v)*g(u,v)=$$f(u,v)g(x-u,y-v) 先將g(u,v)繞其原點旋轉180度,然后平移其原點,u軸上像上平移x, v軸上像上平移y。然后兩個函數相乘積分,得到一個點處的輸出。 圖像處理中的卷積與上面的定義稍微有一點不同。用一個模板和一幅圖像進行卷積,對于圖像上的一個點,讓模板的原點和該點重合,然后模板上的點和圖像上對應的 點相乘,然后各點的積相加,就得到了該點的卷積值。對圖像上的每個點都這樣處理。由于大多數模板都是對稱的,所以模板不旋轉。把一個點的像素值用它周圍的點的像素值的加權平均代替。
++++++++++++++++++++++
卷積的物理意義,解釋的真幽默!有一個七品縣令,喜歡用打板子來懲戒那些市井無賴,而且有個慣例:如果沒犯大罪,只打一板,釋放回家,以示愛民如子。
有一個無賴,想出人頭地卻沒啥指望,心想:既然揚不了善名,出惡名也成啊。怎么出惡名?炒作唄!怎么炒作?找名人呀!他自然想到了他的行政長官——縣令。
無賴于是光天化日之下,站在縣衙門前撒了一泡尿,后果是可想而知地,自然被請進大堂挨了一板子,然后昂首挺胸回家,躺了一天,嘿!身上啥事也沒有!第二天如 法炮制,全然不顧行政長管的仁慈和衙門的體面,第三天、第四天......每天去縣衙門領一個板子回來,還喜氣洋洋地,堅持一個月之久!這無賴的名氣已經 和衙門口的臭氣一樣,傳遍八方了!縣令大人噤著鼻子,呆呆地盯著案子上的驚堂木,擰著眉頭思考一個問題:這三十個大板子怎么不好使捏?......想當初,本老爺金榜題名時,數學可是得了滿分,今天好歹要解決這個問題:——人(系統!)挨板子(脈沖!)以后,會有什么表現(輸出!)?——費話,疼唄!——我問的是:會有什么表現?——看疼到啥程度。像這無賴的體格,每天挨一個板子啥事都不會有,連哼一下都不可能,你也看到他那得意洋洋的嘴臉了(輸出0);如果一次連揍他十個板子,他可 能會皺皺眉頭,咬咬牙,硬挺著不哼(輸出1);揍到二十個板子,他會疼得臉部扭曲,象豬似地哼哼(輸出3);揍到三十個板子,他可能會象驢似地嚎叫,一把 鼻涕一把淚地求你饒他一命(輸出5);揍到四十個板子,他會大小便失禁,勉強哼出聲來(輸出1);揍到五十個板子,他連哼一下都不可能(輸出0)——死 啦!
縣令鋪開坐標紙,以打板子的個數作為X軸,以哼哼的程度(輸出)為Y軸,繪制了一條曲線:——嗚呼呀!這曲線象一座高山,弄不懂弄不懂。為啥那個無賴連挨了三十天大板卻不喊繞命呀?—— 呵呵,你打一次的時間間隔(Δτ=24小時)太長了,所以那個無賴承受的痛苦程度一天一利索,沒有疊加,始終是一個常數;如果縮短打板子的時間間隔(建議 Δτ=0.5秒),那他的痛苦程度可就迅速疊加了;等到這無賴挨三十個大板(t=30)時,痛苦程度達到了他能喊叫的極限,會收到最好的懲戒效果,再多打 就顯示不出您的仁慈了。——還是不太明白,時間間隔小,為什么痛苦程度會疊加呢?——這與人(線性時不變系統)對板子(脈沖、輸入、激 勵)的響應有關。什么是響應?人挨一個板子后,疼痛的感覺會在一天(假設的,因人而異)內慢慢消失(衰減),而不可能突然消失。這樣一來,只要打板子的時 間間隔很小,每一個板子引起的疼痛都來不及完全衰減,都會對最終的痛苦程度有不同的貢獻:t個大板子造成的痛苦程度=Σ(第τ個大板子引起的痛苦*衰減系數)[衰減系數是(t-τ)的函數,仔細品味]數學表達為:y(t)=∫T(τ)H(t-τ)——拿人的痛苦來說卷積的事,太殘忍了。除了人以外,其他事物也符合這條規律嗎?——呵呵,縣令大人畢竟仁慈。其實除人之外,很多事情也遵循此道。好好想一想,鐵絲為什么彎曲一次不折,快速彎曲多次卻會輕易折掉呢?——恩,一時還弄不清,容本官慢慢想來——但有一點是明確地——來人啊,將撒尿的那個無賴抓來,狠打40大板!也可以這樣理解:T(τ)即第τ個板子,H(t-τ)就是第τ個板子引起的痛苦到t時刻的痛苦程度,所有板子加起來就是∫T(τ)H(t-τ)++++++++++++++++++++++
卷積法的原理是根據線性定常電路的性質(齊次性、疊加性、時不變性、積分性等),借助電路的單位沖激響應h(t),求解系統響應的工具,系統的激勵一般都可以表示為沖擊函數和激勵的函數的卷積,而卷積為高等數學中的積分概念。建議你去看看定積分的內容。
特別注意的是:概念中沖擊函數的幅度是由每個矩形微元的面積決定的。總的說來卷積就是用沖擊函數表示激勵函數,然后根據沖擊響應求解系統的零狀態響應。卷積實質上是對信號進行濾波。卷積應該就是求和也就是積分,對于線性時不變的系統,輸入可以分解成很多強度不同的沖激的和的形式(對于時域就是積分了),那么輸出也就是這些沖激分別作用到系統產生的響應的和(或者積分)。所以卷積的物理意義就是表達了時域中輸入,系統沖激響應,以及輸出之間的關系。卷積是在時域求解LTI系統對任意激勵的零狀態響應的好方法,可以避免直接求解復雜的微分方程。從數學上來說卷積就是定義兩個函數的一種乘法。對離散序列來說就是兩個多項式的乘法。物理意義就是沖激響應的線性疊加,所謂沖激響應可以看作是一個函數,另一個函數按沖激信號正交展開。在現實中,卷積代表的是將一種信號搬移到另一頻率中。比如調制。這是頻率卷從數學看,卷積是一種反映兩個序列或函數之間的運算方法;從物理上看,卷積可代表某種系統對某個物理量或輸入的調制或污染;從 信號角度來看,卷積代表了線性系統對輸入信號的響應方式,其輸出就等于系統沖擊函數和信號輸入的卷積,只有符合疊加原理的系統,才有系統沖擊函數的概念, 從而卷積成為系統對輸入在數學上運算的必然形式,沖擊函數實際上是該問題的格林函數解。點激勵源作為強加激勵,求解某個線性問題的解,得到的格林函數即是 系統沖擊響應。所以在線性系統中,系統沖擊響應與卷積存在著必然的聯系。但是卷積本身不過是一個數學運算方法而已。++++++++++++++++++++++
相關分為自相關和互相關,自相關代表信號本身和延遲一段時間以后的相似程度,互相關代表兩個信號的相似程度。卷積是一種運算,相關運算可通過卷積求得。++++++++++++++++++++++
相關的實際意義是什么?它與卷積的區別有是什么?
相關就是求兩個信號的相似程度,相關可以通過卷積求出來,好像g(t)*g(-t)就是g(t)和自己的相關。因為卷積時其中一個信號要翻轉,那么g(t)*g(-t)就相當于求相關我從數學的角度分析一下。信號處理是將一個信號空間映射到另外一個信號空間,通常就是時域到頻域,(還有z域,s域),信號的能量就是函數的范數(信號與函數等同的概念),大家都知 道有個Paserval定理就是說映射前后范數不變,在數學中就叫保范映射,實際上信號處理中的變換基本都是保范映射,只要Paserval定理成立就是 保范映射(就是能量不變的映射)。前面說的意思就是信號處理的任務就是尋找和信號集合對應的一個集合,然后在另外一個集合中分析信號,Fourier變換就是一種,它建立了時域中每個信號函數與頻域中的每個頻譜函數的一一對應關系,這是元素之間的對應。那么運算之間的對應呢,在時域的加法對應頻域中的加法,這就是FT線性性的體現;那么時域的乘法對應什么呢,最后得到的那個表達式我們就把它叫卷積,就是對應的頻域的卷積。簡單來說,卷積是一種重疊關系,也就是說,所得到的結果反映了兩個卷積函數的重疊部分。所以,用一個已知頻段的函數卷積另一個頻段很寬的函數,也就是對后者進行了濾波,后者跟前者重疊的頻段才能很好地通過這個filter.對于時域可以使用乘法器來實現乘法運算,但是頻域的乘法就可以通過時域的卷積操作來完成。卷積是一種積分運算,用來求兩個曲線重疊區域面積。可以看作加權求和,可以用來消除噪聲、特征增強。卷積我覺得就象一把銼刀,它主要是把一些非光滑的函數或算子光滑化。++++++++++++++++++++++
卷積是一種線性運算,圖像處理中常見的mask運算都是卷積,廣泛應用于圖像濾波。卷積關系最重要的一種情況,就是在信號與線性系統或數字信號處理中的卷積定理。利用該定理,可以將時間域或空間域中的卷積運算等價為頻率域的相乘運算,從而利用FFT等快速算法,實現有效的計算,節省運算代價。卷積本身是一種運算,但是應用到信號上,當某個信號通過一個線性系統時,輸出信號就是輸入信號與系統沖擊響應的卷積。卷積是一種線性運算,在信號與線性系統的基礎上出現的。自相關是指信號在1個時刻的瞬時值與另1個時刻的瞬時值之間的依賴關系,是對1個隨機信號的時域描述卷積的理解——外行(數學家)俺寫了那么“精彩”的數學科普沒人看,卻讓不是搞數學的人寫的數學占了上風,杯具啊,實在是杯具。是俺的數學水平太高還是你們的數學欣賞水平太低?亦或俺寫的太專業?這回來點不專業的。
卷積的一個典型例子,其實就是初中就學過的多項式相乘的運算,比如(x*x+3*x+2)(2*x+5)一般計算順序是這樣,(x*x+3*x+2)(2*x+5)= (x*x+3*x+2)*2*x+(x*x+3*x+2)*5= 2*x*x*x+3*2*x*x+2*2*x+ 5*x*x+3*5*x+10然后合并同類項的系數,2 x*x*x3*2+1*5 x*x2*2+3*5 x2*5----------2*x*x*x+11*x*x+19*x+10實際上,從線性代數可以知道,多項式構成一個向量空間,其基底可選為{1,x,x*x,x*x*x,...}如此,則任何多項式均可與無窮維空間中的一個坐標向量相對應,如,(x*x+3*x+2)對應于(1 3 2),(2*x+5)對應于(2,5)。線性空間中沒有定義兩個向量間的卷積運算,而只有加法,數乘兩種運算,而實際上,多項式的乘法,就無法在線性空間中說明。可見線性空間的理論多么局限了。但如果按照我們上面對向量卷積的定義來處理坐標向量,(1 3 2)*(2 5)則有2 3 1_ _ 2 5-------- 22 3 1_ 2 5----- 6+5=112 3 12 5-----4+15 =19_ 2 3 12 5------- 10 或者說,(1 3 2)*(2 5)=(2 11 19 10)回到多項式的表示上來,(x*x+3*x+2)(2*x+5)= 2*x*x*x+11*x*x+19*x+10似乎很神奇,結果跟我們用傳統辦法得到的是完全一樣的。換句話,多項式相乘,相當于系數向量的卷積.其實,琢磨一下,道理也很簡單,卷積運算實際上是分別求 x*x*x ,x*x,x,1的系數,也就是說,他把加法和求和雜合在一起做了。(傳統的辦法是先做乘法,然后在合并同類項的時候才作加法)以x*x的系數為例,得到x*x,或者是用x*x乘5,或者是用3x乘2x,也就是2 3 1_ 2 5----- 6+5=11其實,這正是向量的內積.如此則,卷積運算,可以看作是一串內積運算.既然是一串內積運算,則我們可以試圖用矩陣表示上述過程。[ 2 3 1 0 0 0][ 0 2 3 1 0 0]==A[ 0 0 2 3 1 0][ 0 0 0 2 3 1][0 0 2 5 0 0]' == xb= Ax=[ 2 11 19 10]'采用行的觀點看Ax,則b的每行都是一個內積。A的每一行都是序列[2 3 1]的一個移動位置。顯然,在這個特定的背景下,我們知道,卷積滿足交換,結合等定律,因為,眾所周知的,多項式的乘法滿足交換律,結合律。在一般情形下,其實也成立。在這里,我們發現多項式,除了構成特定的線性空間外,基與基之間還存在某種特殊的聯系,正是這種聯系,給予多項式空間以特殊的性質.在學向量的時候,一般都會舉這個例子,甲有三個蘋果,5個橘子,乙有5個蘋果,三個橘子,則共有幾個蘋果,橘子。老師反復告誡,橘子就是橘子,蘋果就是蘋 果,可不能混在一起。所以有(3,5)+(5,3)=(8,8).是的,橘子和蘋果無論怎么加,都不會出什么問題的,但是,如果考慮橘子乘橘子,或者橘子 乘蘋果,這問題就不大容易說清了。又如復數,如果僅僅定義復數為數對(a,b),僅僅在線性空間的層面看待C2,那就未免太簡單了。實際上,只要加上一條(a,b)*(c,d)=(ac-bd,ad+bc)則情況馬上改觀,復變函數的內容多么豐富多彩,是眾所周知的。另外,回想信號處理里面的一條基本定理,頻率域的乘積,相當于時域或空域信號的卷積。恰好跟這里的情形完全對等。這后面存在什么樣的隱態聯系,需要繼續參詳。從這里看,高等的卷積運算其實不過是一種初等的運算的抽象而已。中學學過的數學里面,其實還蘊涵著許多高深的內容(比如交換代數)。溫故而知新,斯言不謬。其實這道理一點也不復雜,人類繁衍了多少萬年了,但過去n多年,人們只知道男女媾精,乃能繁衍后代。精子,卵子的發現,生殖機制的研究,也就是最近多少年的事情。孔子說,道在人倫日用中,看來我們應該多用審視的眼光看待周圍,乃至自身,才能知其然,而知其所以然。
唐老師用輸液過程解釋卷積的確有點意思,比較容易讓人接受,老邪的方法更簡明易懂,不過老邪的方法可以解釋怎么定義卷積,卻不能說明為什么要定義卷積。如果我沒有記錯,卷積最早來自于信號系統理論,后來被數學家們發揚光大了,而且其威力已經遠遠超出了發明者的初衷。先來看信號處理中如何出現卷積的。假設B是一個系統,其t時刻的輸入為x(t),輸出為y(t),系統的響應函數為h(t),按理說,輸出與輸入的關系應該為Y(t)=h(t)x(t),然而,實際的情況是,系統的輸出不僅與系統在t時刻的響應有關,還與它在t時刻之前的響應有關,不過系統有個衰減過程,所以t1(
-
算法
+關注
關注
23文章
4599瀏覽量
92643 -
卷積
+關注
關注
0文章
95瀏覽量
18499 -
傅立葉變換
+關注
關注
3文章
99瀏覽量
32351
原文標題:卷積的本質及物理意義,解釋的真幽默!
文章出處:【微信號:WW_CGQJS,微信公眾號:傳感器技術】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
有幾個專業名次需要解釋一下。帶寬,DB,諧振,卷積
簡談卷積—幽默笑話談卷積
什么是卷積_卷積的意義
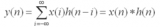
淺析卷積的本質及物理意義
卷積神經網絡的工作原理 卷積神經網絡通俗解釋
亥姆霍茲方程物理意義
傅里葉變換的本質及物理意義 常用傅里葉變換性質
如何通俗易懂地解釋卷積?
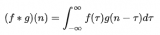




 卷積的本質是什么?有什么物理意義?幽默的給你解釋
卷積的本質是什么?有什么物理意義?幽默的給你解釋












評論