眾所周知,神經網絡可以學習如何表示和處理數字式信息,但是如果在訓練當中遇到超出可接受的數值范圍,它歸納信息的能力很難保持在一個較好的水平。為了推廣更加系統化的數值外推,我們提出了一種新的架構,它將數字式信息表示為線性激活函數,使用原始算術運算符進行運算,并由學習門控制。我們將此模塊稱為神經算術邏輯單元(NALU),類似于傳統處理器中的算術邏輯單元。實驗表明,增強的NALU神經網絡可以學習時間追蹤,使用算術對數字式圖像進行處理,將數字式信息轉為實值標量,執行計算機代碼以及獲取圖像中的目標個數。與傳統的架構相比,我們在訓練過程中不管在數值范圍內還是外都可以更好的泛化,并且外推經常能超出訓練數值范圍的幾個數量級之外。
▌簡介
對數值表示和處理的能力在許多物種中普遍可見,這表明基本的定量推理是智力的一個組成部分。雖然神經網絡可以在給定適當的學習信號的情況下成功地表示和處理數值量,但它們的學習行為缺乏系統的泛化。具體而言,當測試階段的數值超出了訓練階段的數值范圍,即使目標函數很簡單也會導致出錯。這表明學習行為的特點是記憶而不是系統抽象。
在本文中,我們設計了一個偏向于學習系統數值計算的新模塊,該模塊可以與標準的神經網絡體系結構結合使用。我們的策略是將數值表示為無非線性的單個神經元,其中這些單值神經元采用的是類似于加減乘除的運算符來表示,運算符由參數來控制。
神經網絡中的數值外推失效
為了說明標準網絡中的系統性失效,我們展示了各種MLPs在學習標量恒等函數的表現。圖1表明即使采用簡單的框架,所有非線性函數都無法學習到超出訓練范圍外的數量表示。
圖1 MLPs在學習標量恒等函數時的表現
▌神經累加器和神經算術邏輯單元
本文,我們提出了兩種能夠學習以系統的方式去表示和處理數字式信息的模型。第一種模型有支持對積累量進行累加的能力,這是線性外推的理想偏置項。該模型構成了第二個模型的基礎,即支持乘法外推。此模型還闡述了如何將任意算術函數的偏置項有效地融合到端到端模型中。
第一個模型是神經累加器(NAC),它是線性(仿射)層的一種特殊應用,其變換矩陣W只由-1,0和1組成。也就是說,它的輸出是輸入向量中行的加減算法,這也能夠預防層在將輸入映射到輸出時改變數字的表示比例。
由于硬性的約束W矩陣中的每個元素都為{-1,0,0},這使得模型在學習中變得更加困難。為此我們提出了一種W在無參數約束條件下的連續可微分參數化方法: 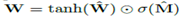 。該方法給梯度下降學習帶來了很大的方便,同時產生一個元素在[-1,1]?并且趨向于-1,0或1的矩陣。圖2描述了一個神經算術邏輯單元(NALU),它可以學習兩個子單元間的加權和,一個能夠進行加減運算,另一個則可以執行乘除以及冪運算,如
。該方法給梯度下降學習帶來了很大的方便,同時產生一個元素在[-1,1]?并且趨向于-1,0或1的矩陣。圖2描述了一個神經算術邏輯單元(NALU),它可以學習兩個子單元間的加權和,一個能夠進行加減運算,另一個則可以執行乘除以及冪運算,如 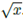 。更重要的優點是,其能夠展示如何在門控的子操作中擴展NAC,從而增強了新類型數值函數的端到端學習。
。更重要的優點是,其能夠展示如何在門控的子操作中擴展NAC,從而增強了新類型數值函數的端到端學習。
圖2(a)神經累加器(b)神經算術邏輯單元
圖2中,NAC是輸入的一次線性變換,變換矩陣是tanh(W)和 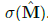 元素的乘積。NALU?使用兩個帶有固定系數的NACs?來進行加減運算(圖2中較小的紫色單元)?以及乘除運算(圖2中較大的紫色單元),并由門(圖2中橙色的單元)來控制。
元素的乘積。NALU?使用兩個帶有固定系數的NACs?來進行加減運算(圖2中較小的紫色單元)?以及乘除運算(圖2中較大的紫色單元),并由門(圖2中橙色的單元)來控制。
▌實驗
我們跨域各種任務領域 (圖像、文本、代碼等),學習信號 (監督和強化學習),結構 (前饋和循環) 進行實驗,結果表明我們提出的模型可以學習到數據中潛在數值性質的表示函數,并推廣到比訓練階段的數值大幾個數量級的數值。相比于線性層我們的模塊有更小的計算偏差。在一個具體實例中,我們的模型超過了目前最先進的圖像計數網絡,值得一提的是,我們所做的修改僅是用我們的模型替換了其最后一個線性層。
簡單的函數學習任務
在這些初始合成實驗中,我們展示了NAC和NALU在學習選擇相關輸入并應用不同算術函數的能力。其中測試任務分為兩類:第一類為靜態任務,即以單個向量一次性輸入;第二類是循環任務,即輸入按時間順序來呈現。通過最小化平方損失來端到端地訓練模型,模型的性能評估由兩個部分組成:訓練范圍內(插值)的留存值和訓練范圍外(外推)的值。表1表明了幾種標準體系結構在插值情況下成功完成任務,但在進行外推時都沒有成功。而不管是在插值還是外推上,NAC都成功地建立加法和減法模型,NALU在乘法運算上也獲得成功。
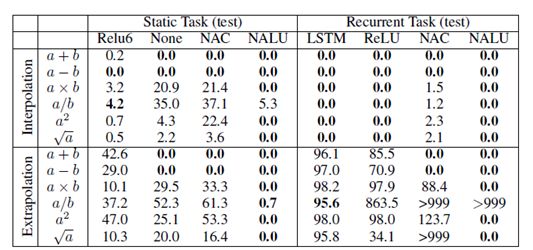
表 1 靜態和循環任務的插值和外推誤差率
MNIST 計數和算術任務
在這項任務中,我們給模型10個隨機選擇的MNIST數字,要求模型輸出觀察到的數值和每種類型的圖像數量,在MNIST數字加法任務中,模型還必須學會計算所觀察到的數字之和。在插值(長度為10)和外推(長度為100和長度為1000)任務上測試模型的計數和算術的性能。表2表明標準體系結構在插值任務上成功,但在外推任務上失敗。但是NAC和NALU都能很好地完成插值和外推任務。
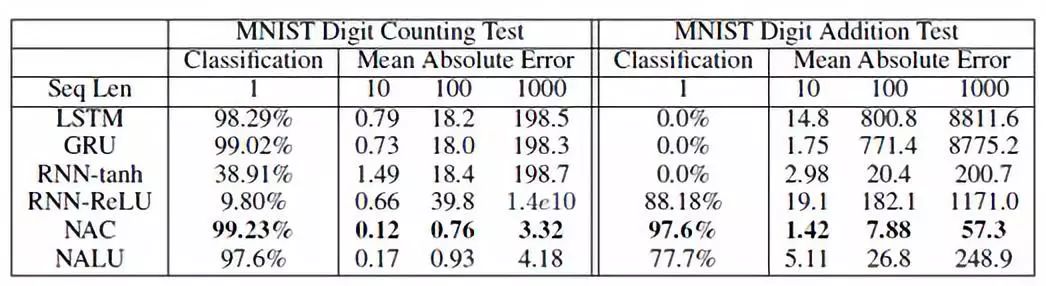
表2 長度為1,100,1000的序列的 MNIST 計數和加法任務的準確度
語言到數字的翻譯任務
為了測試數字詞語的表示是否是以系統的形式來學習,我們設計了一個新的翻譯任務:將文本數字表達式(例如五百一十五)轉換為標量表示(515)。訓練和測試的數字范圍在0到1000之間,其中訓練集、驗證集和測試集的示例分別為169、200和631。在該數據集上訓練的所有網絡都以embedding層開始,通過LSTM進行編碼,最后接一個NAC或NALU。表3表明了LSTM + NAC在訓練和測試集上都表現不佳。LSTM + NALU可以大幅度地實現最佳的泛化性能,這說明乘數對于此任務來說非常重要。這里還給出了一個NALU測試的例子如圖3所示。

表3將數字串轉換為標量的平均絕對誤差(MSE)比較

圖3 NALU的預測樣例
程序評估
程序評估部分我們考慮兩個方面:第一個為簡單地添加兩個大整數,第二個為包含若干個操作(條件聲明、加和減)。此次評估專注于外推部分即:網絡是否可以學習一種推廣到更大數值范圍的解決方案。用[0,100)范圍內的兩位數整數來訓練,并用三位或四位的隨機整數來評估。圖4比較了四種不同模型(UGRNN、LSTM、DNC和NALU)的評估結果,其中只有NALU是能夠推廣到更大的數字。我們可以看到即使域增加了兩個數量級,外推效果也是較為穩定。
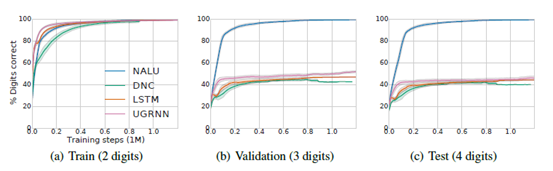
圖4簡單的程序評估,外推到更大的值
學習在網格世界環境中追蹤時間
到目前為止,在所有實驗中,我們訓練的模型已經可以進行數值預測了。然而,正如引言部分所說,系統化的數值推算似乎是各種智能行為的基礎。因此,我們進行了一項任務,測試NAC能否被RL-trained智能體“內部”使用。
如圖5所示,該任務中,每一幀都是從初始值開始(t=0),紅色的目標隨機定位于5*5的網絡世界方格中。每個時間步中,智能體接收一個56*56像素網格以表示整個網格世界環境狀態,并且必須從{上移,下移,左移,右移,忽略}選擇其中的一個操作。測試開始前,智能體還會接收一個數字(整數)指令T ,用來傳達代理到底目的地的確切時間。
達到最大幀時,獎勵m,智能體必須選擇操作并四處移動。第一次移動至紅色區域時就是t=T的時候,當智能體到達紅色區域或者時間結束時(t=L)訓練結束。
圖5網格世界環境中時間追蹤任務
MNIST 奇偶校驗預測任務和消融研究
在我們的最后一項任務:MNIST奇偶校驗中,輸入和輸出都不是直接用數字提供的,而是隱式地對數字量進行推理。在這個實驗中,NAC或其變體取代了由Segui等人提出的模型中的最后一個線性層。我們系統地研究了每個約束的重要性。表4總結了變體模型的性能,我們可以看到去除偏置項和運用非線性權重的方法顯著提高了端到端模型的準確性,NAC將先前最佳結果的誤差減少了54%。
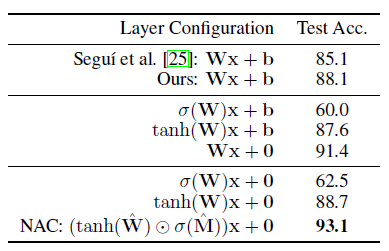
表4關于MNIST奇偶校驗任務的affine層和NAC之間的消融研究
▌結論
目前,神經網絡中數值模擬方法還不夠完善,因為數值表示方法不能夠對其訓練觀察到的數值范圍外對信息進行較好的概括。本文,我們已經展示了NAC與NALU是如何解這兩個不足之處,它改善了數值表示方法以及數值范圍外的函數。然而,NAC或NALU不太可能很完美的解決每一個任務。但它們可以被作為解決創建模型時目標函數存在偏置項的一種通用策略。該策略是由我們提出的單元神經數值表示方式實現的,它允許將任意(可微)數值函數添加到模塊中,并通過學習門進行控制。
-
神經網絡
+關注
關注
42文章
4765瀏覽量
100550 -
神經元
+關注
關注
1文章
363瀏覽量
18438
原文標題:前沿 | DeepMind 最新研究——神經算術邏輯單元,有必要看一下!
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于可編程邏輯器件和VHDL語言實現算術邏輯單元的設計
FPGA基礎學習筆記--組合邏輯電路-算術運算電路
算術邏輯單元ALU四個要素
恩智浦eIQ? Neutron神經處理單元
TMS320F24X 指令集累加器、算術與邏輯指令附件
多功能算術/邏輯運算單元(ALU) ,什么是多功能算術/邏輯
DeepMind最新提出“神經算術邏輯單元”,旨在解決神經網絡數值模擬能力不足的問題
51單片機的算術和邏輯運算功能介紹
用VHDL語言創建一個8位算術邏輯單元(ALU)





 什么是神經算術邏輯單元?
什么是神經算術邏輯單元?










評論