濃縮就是精華。想要把書寫厚很容易，想要寫薄卻非常難。現(xiàn)在已經(jīng)有這么多經(jīng)典的機器學習算法，如果能抓住它們的核心本質(zhì)，無論是對于理解還是對于記憶都有很大的幫助，還能讓你更可能通過面試。在本文中，SIGAI將用一句話來總結每種典型的機器學習算法，幫你抓住問題的本質(zhì)，強化理解和記憶。下面我們就開始了。

貝葉斯分類器

核心：將樣本判定為后驗概率最大的類

貝葉斯分類器直接用貝葉斯公式解決分類問題。假設樣本的特征向量為x，類別標簽為y，根據(jù)貝葉斯公式，樣本屬于每個類的條件概率（后驗概率）為：

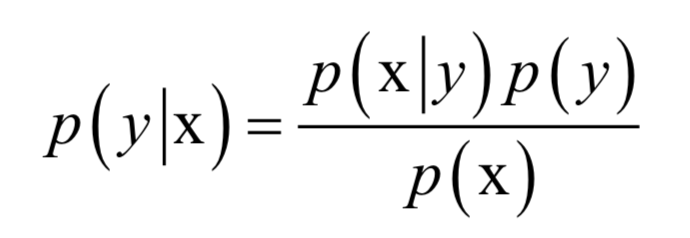
分母p(x)對所有類都是相同的，分類的規(guī)則是將樣本歸到后驗概率最大的那個類，不需要計算準確的概率值，只需要知道屬于哪個類的概率最大即可，這樣可以忽略掉分母。分類器的判別函數(shù)為：

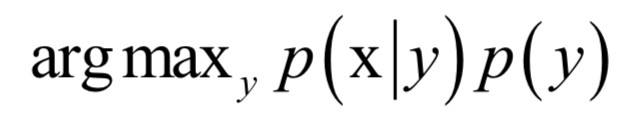
在實現(xiàn)貝葉斯分類器時，需要知道每個類的條件概率分布p(x|y)即先驗概率。一般假設樣本服從正態(tài)分布。訓練時確定先驗概率分布的參數(shù)，一般用最大似然估計，即最大化對數(shù)似然函數(shù)。

貝葉斯分分類器是一種生成模型，可以處理多分類問題，是一種非線性模型。

決策樹

核心：一組嵌套的判定規(guī)則

決策樹在本質(zhì)上是一組嵌套的if-else判定規(guī)則，從數(shù)學上看是分段常數(shù)函數(shù)，對應于用平行于坐標軸的平面對空間的劃分。判定規(guī)則是人類處理很多問題時的常用方法，這些規(guī)則是我們通過經(jīng)驗總結出來的，而決策樹的這些規(guī)則是通過訓練樣本自動學習得到的。下面是一棵簡單的決策樹以及它對空間的劃分結果：

訓練時，通過最大化Gini或者其他指標來尋找最佳分裂。決策樹可以輸特征向量每個分量的重要性。

決策樹是一種判別模型，既支持分類問題，也支持回歸問題，是一種非線性模型（分段線性函數(shù)不是線性的）。它天然的支持多分類問題。

kNN算法

核心：模板匹配，將樣本分到離它最相似的樣本所屬的類

kNN算法本質(zhì)上使用了模板匹配的思想。要確定一個樣本的類別，可以計算它與所有訓練樣本的距離，然后找出和該樣本最接近的k個樣本，統(tǒng)計這些樣本的類別進行投票，票數(shù)最多的那個類就是分類結果。下圖是kNN算法的示意圖：

在上圖中有紅色和綠色兩類樣本。對于待分類樣本即圖中的黑色點，尋找離該樣本最近的一部分訓練樣本，在圖中是以這個矩形樣本為圓心的某一圓范圍內(nèi)的所有樣本。然后統(tǒng)計這些樣本所屬的類別，在這里紅色點有12個，圓形有2個，因此把這個樣本判定為紅色這一類。

kNN算法是一種判別模型，即支持分類問題，也支持回歸問題，是一種非線性模型。它天然的支持多分類問題。kNN算法沒有訓練過程，是一種基于實例的算法。

PCA

核心：向重構誤差最小（方差最大）的方向做線性投影

PCA是一種數(shù)據(jù)降維和去除相關性的方法，它通過線性變換將向量投影到低維空間。對向量進行投影就是讓向量左乘一個矩陣得到結果向量，這是線性代數(shù)中講述的線性變換：

y = Wx

降維要確保的是在低維空間中的投影能很好的近似表達原始向量，即重構誤差最小化。下圖是主分量投影示意圖：

在上圖中樣本用紅色的點表示，傾斜的直線是它們的主要變化方向。將數(shù)據(jù)投影到這條直線上即完成數(shù)據(jù)的降維，把數(shù)據(jù)從2維降為1維。計算最佳投影方向時求解的最優(yōu)化問題為：

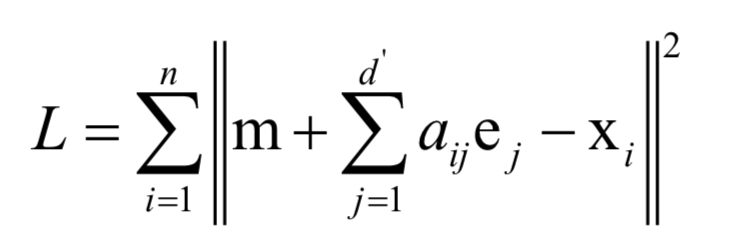
最后歸結為求協(xié)方差矩陣的特征值和特征向量：

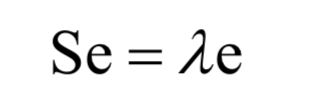
PCA是一種無監(jiān)督的學習算法，它是線性模型，不能直接用于分類和回歸問題。

LDA

核心：向最大化類間差異、最小化類內(nèi)差異的方向線性投影

線性鑒別分析的基本思想是通過線性投影來最小化同類樣本間的差異，最大化不同類樣本間的差異。具體做法是尋找一個向低維空間的投影矩陣W，樣本的特征向量x經(jīng)過投影之后得到的新向量：

y = Wx

同一類樣投影后的結果向量差異盡可能小，不同類的樣本差異盡可能大。直觀來看，就是經(jīng)過這個投影之后同一類的樣本進來聚集在一起，不同類的樣本盡可能離得遠。下圖是這種投影的示意圖：

上圖中特征向量是二維的，我們向一維空間即直線投影，投影后這些點位于直線上。在上面的圖中有兩類樣本，通過向右上方的直線投影，兩類樣本被有效的分開了。綠色的樣本投影之后位于直線的下半部分，紅色的樣本投影之后位于直線的上半部分。

訓練時的優(yōu)化目標是類間差異與類內(nèi)差異的比值：

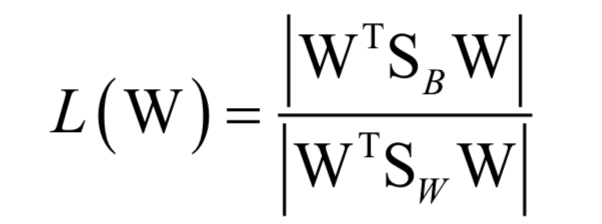
最后歸結于求解矩陣的特征值與特征向量：

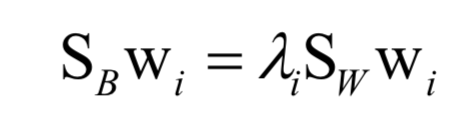
LDA是有監(jiān)督的機器學習算法，在計算過程中利用了樣本標簽值。這是一種判別模型，也是線性模型。LDA也不能直接用于分類和回歸問題，要對降維后的向量進行分類還需要借助其他算法，如kNN。

LLE（流形學習）

核心：用一個樣本點的鄰居的線性組合近似重構這個樣本，將樣本投影到低維空間中后依然保持這種線性組合關系

局部線性嵌入（簡稱LLE）將高維數(shù)據(jù)投影到低維空間中，并保持數(shù)據(jù)點之間的局部線性關系。其核心思想是每個點都可以由與它相近的多個點的線性組合來近似，投影到低維空間之后要保持這種線性重構關系，并且有相同的重構系數(shù)。

算法的第一步是求解重構系數(shù)，每個樣本點xi可以由它的鄰居線性表示，即如下最優(yōu)化問題：

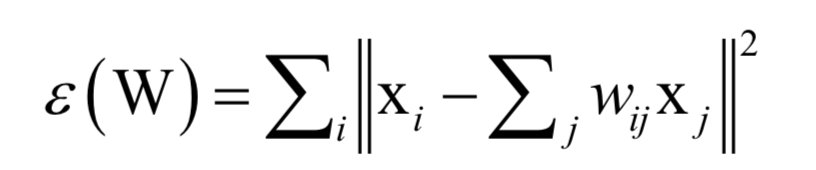
這樣可以得到每個樣本點與它鄰居節(jié)點之間的線性組合系數(shù)。接下來將這個組合系數(shù)當做已知量，求解下面的最優(yōu)化問題完成向量投影：

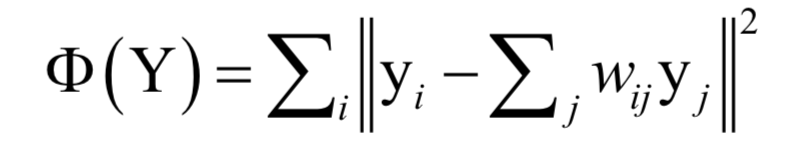
這樣可以得到向量y，這就是投影之后的向量。

LLE是一種無監(jiān)督的機器學習算法，它是一種非線性降維算法，不能直接用于分類或者回歸問題。

等距映射（流形學習）

核心：將樣本投影到低維空間之后依然保持相對距離關系

等距映射使用了微分幾何中測地線的思想，它希望數(shù)據(jù)在向低維空間映射之后能夠保持流形上的測地線距離。所謂測地線，就是在地球表面上兩點之間的最短距離對應的那條弧線。直觀來看，就是投影到低維空間之后，還要保持相對距離關系，即投影之前距離遠的點，投影之后還要遠，投影之前相距近的點，投影之后還要近。

我們可以用將地球儀的三維球面地圖投影為二維的平面地圖來理解：

投影成平面地圖后為：

在投影之前的地球儀上，美國距離中國遠，泰國距離中國近，投影成平面地圖之后，還要保持這種相對遠近關系。

等距映射是一種無監(jiān)督學習算法，是一種非線性降維算法。

人工神經(jīng)網(wǎng)絡

核心：一個多層的復合函數(shù)

人工神經(jīng)網(wǎng)絡在本質(zhì)上是一個多層的復合函數(shù)：

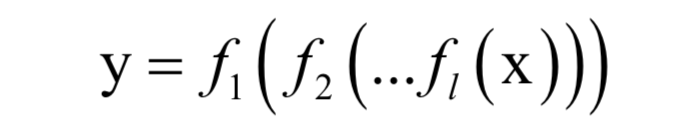
它實現(xiàn)了從向量x到向量y的映射。由于使用了非線性的激活函數(shù)f，這個函數(shù)是一個非線性函數(shù)。

神經(jīng)網(wǎng)絡訓練時求解的問題不是凸優(yōu)化問題。反向傳播算法由多元復合函數(shù)求導的鏈式法則導出。

標準的神經(jīng)網(wǎng)絡是一種有監(jiān)督的學習算法，是一種非線性模型，它既可以用于分類問題，也可以用于回歸問題，天然的支持多分類問題。

支持向量機

核心：最大化分類間隔的線性分類器（不考慮核函數(shù)）

支持向量機的目標是尋找一個分類超平面，它不僅能正確的分類每一個樣本，并且要使得每一類樣本中距離超平面最近的樣本到超平面的距離盡可能遠。

訓練時求解的原問題為：

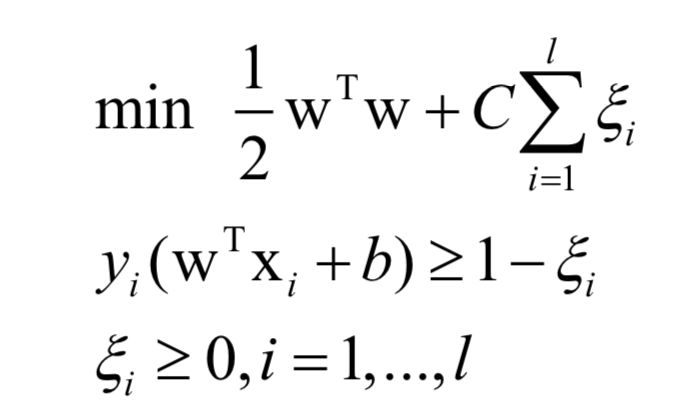
對偶問題為：

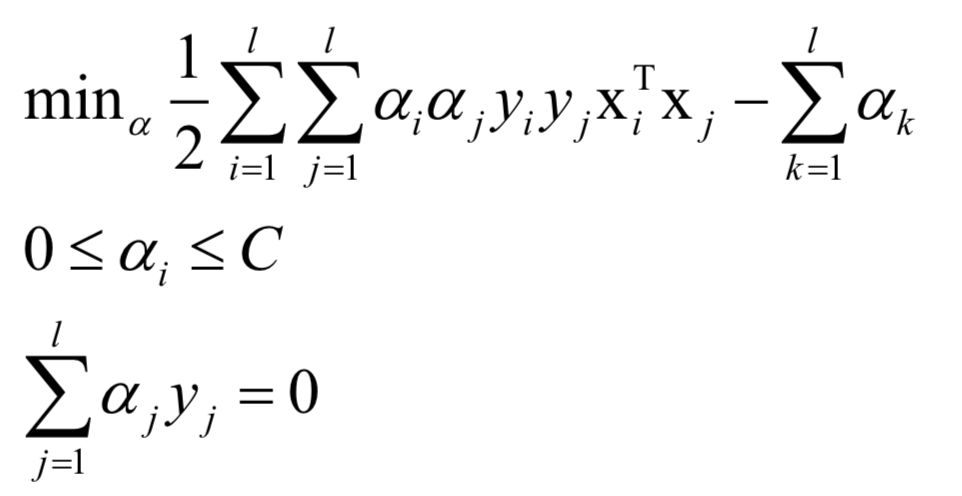
對于分類問題，預測函數(shù)為：

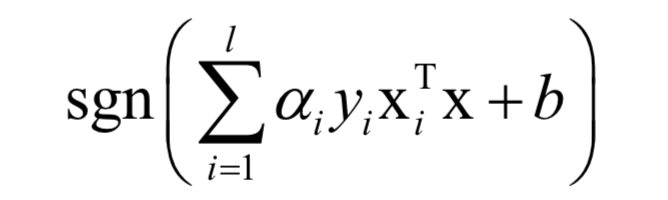
如果不使用非線性核函數(shù)，SVM是一個線性模型。使用核函數(shù)之后，SVM訓練時求解的對偶問題為：

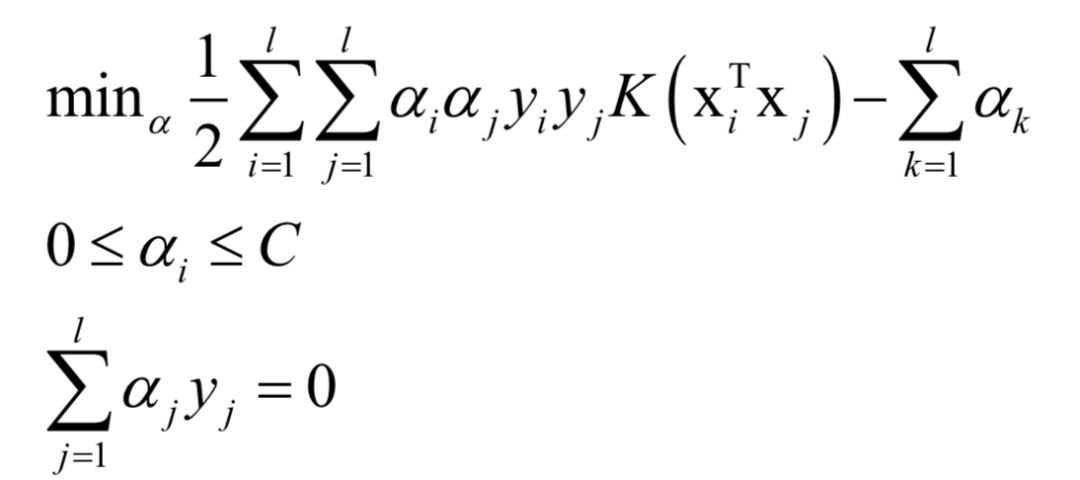
對于分類問題，預測函數(shù)為：

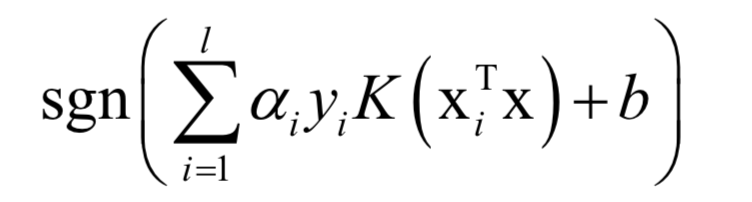
如果使用非線性核，SVM是一個非線性模型。

訓練時求解的問題是凸優(yōu)化問題，求解采用了SMO算法，這是一種分治法，每次挑選出兩個變量進行優(yōu)化，其他變量保持不動。選擇優(yōu)化變量的依據(jù)是KKT條件，對這兩個變量的優(yōu)化是一個二次函數(shù)極值問題，可以直接得到公式解。

SVM是一種判別模型。它既可以用于分類問題，也可以用于回歸問題。標準的SVM只能支持二分類問題，使用多個分類器的組合，可以解決多分類問題。

logistic回歸

核心：直接從樣本估計出它屬于正負樣本的概率

通過先將向量進行線性加權，然后計算logistic函數(shù)，可以得到[0,1]之間的概率值，它表示樣本x屬于正樣本的概率：

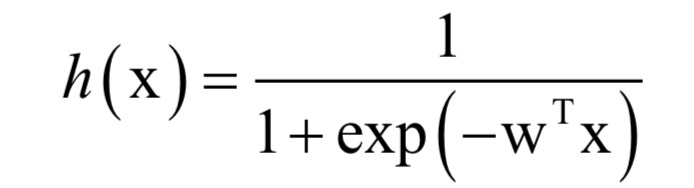
正樣本標簽值為1，負樣本為0。訓練時，求解的的是對數(shù)似然函數(shù)：

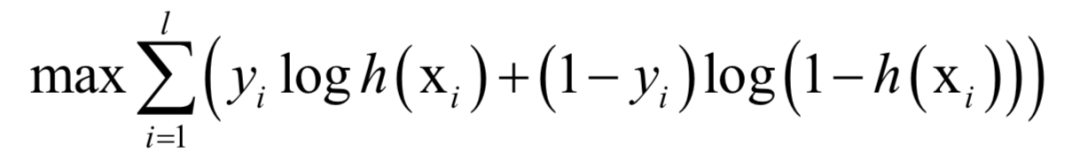
這是一個凸優(yōu)化問題，求解時可以用梯度下降法，也可以用牛頓法。

logistic回歸是一種判別模型，需要注意的是它是一種線性模型，用于二分類問題。

隨機森林

核心：用有放回采樣的樣本訓練多棵決策樹，訓練決策樹的每個節(jié)點是只用了無放回抽樣的部分特征，預測時用這些樹的預測結果進行投票

隨機森林是一種集成學習算法，它由多棵決策樹組成。這些決策樹用對訓練樣本集隨機抽樣構造出樣本集訓練得到。隨機森林不僅對訓練樣本進行抽樣，還對特征向量的分量隨機抽樣，在訓練決策樹時，每次分裂時只使用一部分抽樣的特征分量作為候選特征進行分裂。

對于分類問題，一個測試樣本會送到每一棵決策樹中進行預測，然后投票，得票最多的類為最終分類結果。對于回歸問題隨機森林的預測輸出是所有決策樹輸出的均值。

假設有n個訓練樣本。訓練每一棵樹時，從樣本集中有放回的抽取n個樣本，每個樣本可能會被抽中多次，也可能一次都沒抽中。用這個抽樣的樣本集訓練一棵決策樹，訓練時，每次尋找最佳分裂時，還要對特征向量的分量采樣，即只考慮部分特征分量。

隨機森林是一種判別模型，既支持分類問題，也支持回歸問題，并且支持多分類問題。這是一種非線性模型。

AdaBoost算法

核心：用多個分類器的線性組合來預測，訓練時重點關注錯分的樣本，準確率高的弱分類器權重大

AdaBoost算法的全稱是自適應boosting（Adaptive Boosting），是一種用于二分類問題的算法，它用弱分類器的線性組合來構造強分類器。弱分類器的性能不用太好，僅比隨機猜測強，依靠它們可以構造出一個非常準確的強分類器。強分類器的計算公式為：

其中x是輸入向量，F(xiàn)(x)是強分類器，ft(x)是弱分類器，at是弱分類器的權重，T為弱分類器的數(shù)量，弱分類器的輸出值為+1或-1，分別對應正樣本和負樣本。分類時的判定規(guī)則為：

sgn(F(x))

強分類器的輸出值也為+1或-1，同樣對應于正樣本和負樣本。

訓練時，依次訓練每一個若分類器，并得到它們的權重值。在這里，訓練樣本帶有權重值，初始時所有樣本的權重相等，在訓練過程中，被前面的弱分類器錯分的樣本會加大權重，反之會減小權重，這樣接下來的弱分類器會更加關注這些難分的樣本。弱分類器的權重值根據(jù)它的準確率構造，精度越高的弱分類器權重越大。

AdaBoost算法從廣義加法模型導出，訓練時求解的是指數(shù)損失函數(shù)的極小值：

L(y, F(x)) = exp(-yF(x))

求解時采用了分階段優(yōu)化，先得到弱分類器，然后確定弱分類器的權重值。

標準的AdaBoost算法是一種判別模型，只能支持二分類問題。它的改進型可以處理多分類問題。

卷積神經(jīng)網(wǎng)絡

核心：一個共享權重的多層復合函數(shù)

卷積神經(jīng)網(wǎng)絡在本質(zhì)上也是一個多層復合函數(shù)，但和普通神經(jīng)網(wǎng)絡不同的是它的某些權重參數(shù)是共享的，另外一個特點是它使用了池化層。訓練時依然采用了反向傳播算法，求解的問題不是凸優(yōu)化問題。

和全連接神經(jīng)網(wǎng)絡一樣，卷積神經(jīng)網(wǎng)絡是一個判別模型，它既可以用于分類問題，也可以用用于回歸問題，并且支持多分類問題。

循環(huán)神經(jīng)網(wǎng)絡

核心：綜合了復合函數(shù)和遞推數(shù)列的一個函數(shù)

和普通神經(jīng)網(wǎng)絡最大的不同在于，循環(huán)神經(jīng)網(wǎng)絡是一個遞推的數(shù)列，因此具有了記憶功能。回憶我們高中時所學的等差數(shù)列：

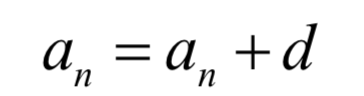
一旦數(shù)列的首項a0以及公差d已經(jīng)確定，則后面的各項也確定了，這樣后面各項完全沒有機會改變自己的命運。循環(huán)神經(jīng)網(wǎng)絡也是這樣一個遞推數(shù)列，后一項由前一項的值決定，但除此之外還接受了一個次的輸入值，這樣本次的輸出值既和之前的數(shù)列值有關，由于當前時刻的輸入值有關，有機會通過當前輸入值改變自己的命運：

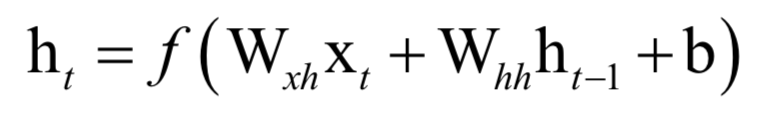
和其他類型的神經(jīng)網(wǎng)絡一樣，循環(huán)神經(jīng)網(wǎng)絡是一個判別模型，既支持分類問題，也支持回歸問題，并且支持多分類問題。

K均值算法

核心：把樣本分配到離它最近的類中心所屬的類，類中心由屬于這個類的所有樣本確定

k均值算法是一種無監(jiān)督的聚類算法。算法將每個樣本分配到離它最近的那個類中心所代表的類，而類中心的確定又依賴于樣本的分配方案。這是一個先有雞還是先有蛋的問題。

在實現(xiàn)時，先隨機初始化每個類的類中心，然后計算樣本與每個類的中心的距離，將其分配到最近的那個類，然后根據(jù)這種分配方案重新計算每個類的中心。這也是一種分階段優(yōu)化的策略。

k均值算法要求解的問題是一個NPC問題，只能近似求解，有陷入局部極小值的風險。