設計新的結構時,你是否曾經對如何獲得最優形狀感到迷茫?如果是這樣,那么你一定會樂意學習一種非常有用的稱為“形狀優化”的技術,擁有了這項技術,你的 COMSOL Multiphysics 建模技能就又提高了一步。今天我們將探討形狀優化的概念,并借助一個典型案例來演示其用法。
形狀優化的背景
工程師、研究人員和科研人員們一直在努力改進設計。優化是指這樣一種理念,即改變零件尺寸和材料屬性等模型輸入數據,實現某些指標的提升,同時還滿足一組約束條件。COMSOL Multiphysics 中的優化模塊是處理此類問題的得力工具。
尺寸優化是其中一種比較常見的優化技巧。這個方法要求直接更改 CAD 尺寸,實現質量最小化,可參考我們的支架的優化教程。在這個支架示例中,我們利用所謂的無梯度技術調整尺寸,同時還考慮了以下約束:尺寸間關系、峰值應力以及最低固有特征頻率。這些技術會根據不同的目標函數和約束類型采用不同的處理方法,因此相當靈活。不過,這些技術有一個缺點:必須不斷地對零件重新剖分網格,從而使設計變量從數值上逼近目標函數和約束的靈敏度。
如我們在以前的一篇文章中討論的,在使用變形幾何接口時,如果幾何發生變化,那么也可以通過分析計算設計靈敏度。進一步來講,基于梯度的求解器無需重新剖分網格,即利用靈敏度優化零件的尺寸,這是我們在設計電容器一文中重點討論的內容。回顧以上兩篇文章有助于理解我們今天要使用的功能。
形狀優化是對以前討論的相關概念的一個延伸,其中不僅考慮了簡單的尺寸更改,還涉及到形狀的總體改變。結構的形狀受控于一組設計參數,這些參數使用了一組能描述任意形狀的基函數。在下文中,我們將結合具體案例進行探討。
形狀優化問題:梁的厚度
調整懸臂梁的厚度是一個典型的形狀優化問題,我們以此入手來進行探討:調整懸臂厚度并使其質量最小化,同時滿足自由端上撓度峰值的約束。梁的初始厚度均勻,但頂部表面上分布的載荷不均勻,請參考下圖。
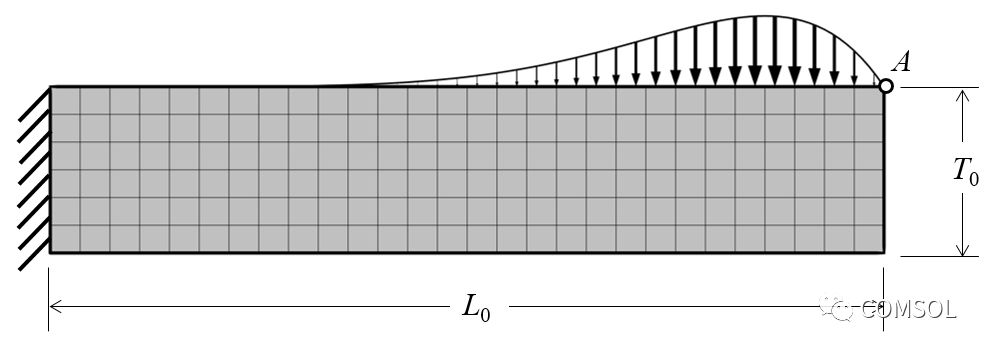
載荷不均勻的懸臂梁,點 A 的撓度不應超過指定值。圖中還顯示了網格。
我們先選擇設計變量。在懸臂端,梁的長度和厚度固定,長度方向上梁的厚度可以改變。根據初始配置改變厚度會稍微更簡單些。不過,我們引入了函數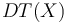 ,它在長度方向上的初始值為零。
,它在長度方向上的初始值為零。
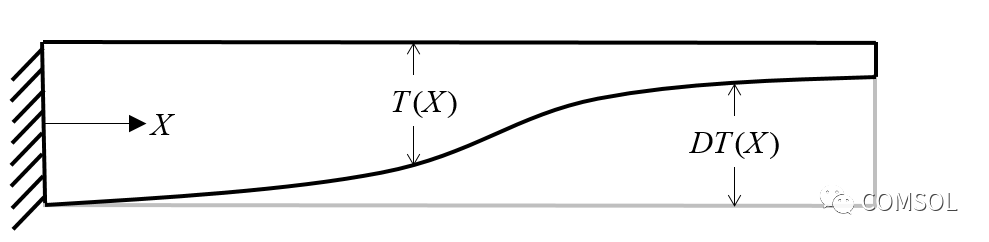
優化問題研究梁的厚度變化。
在這里,我們選擇用一組四階伯恩斯坦多項式表示厚度變化:
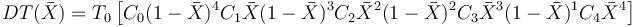
用歸一化尺寸表示: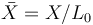 。請注意,此函數已按比例縮小了,這樣多項式系數的數量級接近 1。這樣做也是為了實現縮放的目的。
。請注意,此函數已按比例縮小了,這樣多項式系數的數量級接近 1。這樣做也是為了實現縮放的目的。
因為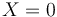 ?時梁的厚度已指定,因此在固定?
?時梁的厚度已指定,因此在固定?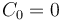 ?時,
?時,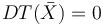 ,所以這一項可略去。在遠端,我們添加了一個約束條件:梁不能太薄,即?
,所以這一項可略去。在遠端,我們添加了一個約束條件:梁不能太薄,即?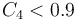 。
。
至于中間區域,我們也希望添加一些約束,進一步限制設計空間。可以添加約束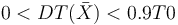 。不過,這一約束有個缺陷:梁的厚度會忽薄忽厚。但是根據基本原理,我們知道這種情況不合常理,在長度方向增加梁的厚度毫無益處。我們就對其導數添加約束:
。不過,這一約束有個缺陷:梁的厚度會忽薄忽厚。但是根據基本原理,我們知道這種情況不合常理,在長度方向增加梁的厚度毫無益處。我們就對其導數添加約束: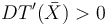 。這個約束迫使梁的厚度沿長度單調增加,隨之還帶來的好處是很自然地滿足了約束條件:
。這個約束迫使梁的厚度沿長度單調增加,隨之還帶來的好處是很自然地滿足了約束條件: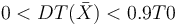 。
。
還要考慮另一個約束:梁一端上點的位移。我們希望點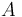 ?的位移量不超過指定值?
?的位移量不超過指定值?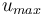 。根據以上信息,我們現在的優化問題就比較完整了:
。根據以上信息,我們現在的優化問題就比較完整了:
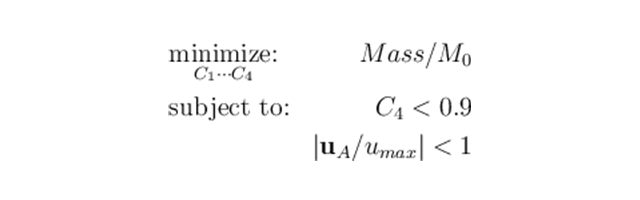
目標函數針對梁的初始質量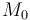 ?所作的歸一化已完成,目標函數已縮放,其階次為 1。類似地,梁端部的位移量?
?所作的歸一化已完成,目標函數已縮放,其階次為 1。類似地,梁端部的位移量?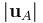 ?針對容許的最大位移?
?針對容許的最大位移?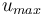 ?進行歸一化,它應當小于 1。現在我們來看一看如何在 COMSOL Multiphysics 中使用“優化模塊”實現此類問題。
?進行歸一化,它應當小于 1。現在我們來看一看如何在 COMSOL Multiphysics 中使用“優化模塊”實現此類問題。
在 COMSOL Multiphysics 中實現這個問題
我們先從初步設計開始,即一個長度固定、厚度均勻的梁。梁一端設計為懸臂式,頂部表面的載荷不均勻,其變化遵循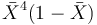 。我們希望先引入厚度變化的函數。之前描述的多項式函數是變量?DT,如下方截圖所示。表達式?Xg?指最初未變形幾何的?x?維度。此函數在歸一化的?x?方向上的導數是變量?dDTdX。兩個全局參數?L0?和?T0?定義長度和最大厚度。
。我們希望先引入厚度變化的函數。之前描述的多項式函數是變量?DT,如下方截圖所示。表達式?Xg?指最初未變形幾何的?x?維度。此函數在歸一化的?x?方向上的導數是變量?dDTdX。兩個全局參數?L0?和?T0?定義長度和最大厚度。
屏幕截圖顯示厚度變化的函數及其導數。
有關厚度變化的變量用在變形幾何接口中,定義梁的總體積如何隨厚度變化而變化。因為只有厚度變化,所以可以使用簡單的線性映射,如下圖所示。
梁內的位移就指定完畢。
現在通過優化接口建立優化問題,其中可以很輕松地創建比較復雜的含多個約束的優化問題。相關設置顯示在下方的屏幕截圖中,先設置目標函數。積分目標特征對材料密度在建模域進行積分,并針對初始零件質量進行歸一化。
優化的目標是質量最小化。
全局控制變量特征的設置如下所示。四個變量C1、C2、C3和C4的初始值為零,相當于梁的初始形狀。對C4的約束是施加了一個上界,所有變量的縮放比例均為 1。
控制變量及其界限和縮放比例的定義。
接著,將逐點不等式約束特征施加到域的底部邊界。該特征強制每一點的位移函數的導數均為正,從而確保函數單調增加。
通過逐點不等式約束對沿梁長度的導數施加約束。
最后,對梁遠端點的峰值位移施加約束,使其小于最大指定值。可通過點求和不等式約束特征設置該值。
對歸一化的峰值位移施加約束。
至此,我們的優化問題基本創建完畢。最后一步是將優化特征添加到研究序列,選擇基于梯度的 SNOPT 求解器,經證實該求解器能最快速地處理我們的問題。所有其他設置保留默認值。目標函數和約束自動取自優化接口。
相關的優化求解器設置。
下圖繪制了結果。其中已顯示根據上述步驟得到的最優形狀。端部的位移最大,厚度沿長度單調增加。我們預計幾何會變形,因此使用了映射網格。
優化后梁的形狀,施加不均勻載荷和約束后實現了質量最小化。其中繪制了位移場,以及施加的載荷分布和網格。
使用形狀優化設計新結構的總結
或許我們自己會疑惑,如何能確定以上的結構真正實現了最優化。因此我們強烈建議進行網格細化研究,嘗試不斷細化網格,以了解其解如何收斂。研究基函數的收斂性也是非常合理的做法。我們可以使用高階伯恩斯坦基函數并比較結果。不過,這樣做可能會導致龍格現象,還會使收斂緩慢。
將原區間細分為多個子區間,在每個子區間(分段多項式)使用不同的較低階形函數,可規避此類問題。除了伯恩斯坦基函數外,我們還可以應用其他基函數,如切比雪夫多項式和傅立葉基函數。號角優化形狀教程重點討論了使用傅立葉基函數的案例,該教程可從“案例下載”中下載。
本篇文章討論的案例中,所包含的變形十分簡單。在涉及更復雜的變形時,需要花更多心思考慮如何定義變形映射。在計算非常復雜的變形時,添加輔助方程也會很有幫助。如果你對使用這些形狀優化技術有任何疑問,或者希望將優化模塊加到自己的建模工具套件中,請聯系我們。
-
函數
+關注
關注
3文章
4306瀏覽量
62431 -
COMSOL
+關注
關注
34文章
93瀏覽量
55687
原文標題:借助 COMSOL “優化模塊”獲取工程設計的最優形狀
文章出處:【微信號:COMSOL-China,微信公眾號:COMSOL】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
教你設計不規則形狀的PCB
大一學生,對fpga的學習 感到迷茫,望前人指點。
labview提取圖像中特定形狀的區域并測量其質心
設計一個SpaceX星艦形狀的PCB
設計了一個定制形狀的圣誕樹
基于形狀上下文的人臉匹配算法
帶形狀參數的曲線曲面的構造
基于復雜網絡模型的形狀描述和識別方法
如何使用最優最小生成樹進行三維模型形狀優化方法的詳細資料說明
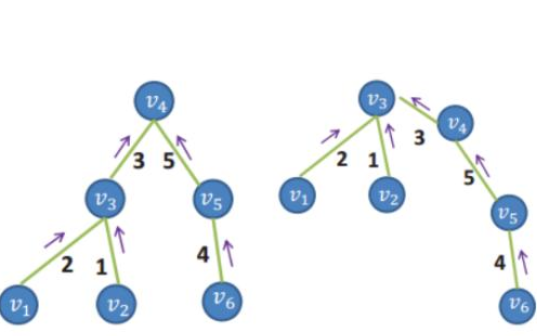




 如何獲得最優形狀感到迷茫?形狀優化的概念,并借助一個典型案例來演示其用法
如何獲得最優形狀感到迷茫?形狀優化的概念,并借助一個典型案例來演示其用法











評論