摘 要:研究了具有不確定參數非線性系統的穩定最優模糊保代價控制問題。采用T-S模糊模型描述非線性系統,對具有范數有界,時變參數不確定性的非線性系統,得到了存在穩定最優模糊保代價控制器的充分條件,并推算出了相應的線性矩陣不等式(LMI)形式。建立了永磁同步電動機混沌系統的T-S模型,采用最優模糊保代價控制器進行控制,針對不含參數不確定性和含有參數不確定性兩種情況進行仿真研究,均得到滿意的控制效果。
1 引言
混沌控制是當前混沌運動研究的一個新領域。是實現混沌應用的關鍵環節。多年來,人們對混沌運動的性質產生了一些廣為接受的認識,即混沌軌道的長期趨勢是不可預言的,并且混沌運動是難以控制的。1990年E.Ott、C.Grebogi和J.A.Yorke提出控制混沌的思想(OGY控制)產生廣泛影響。以后十年,新的研究成果不斷涌現。以上方案無須改變系統固有參數,即可實現對混沌系統的有效控制,但是,要求系統參數是定常的。當混沌系統具有不確定參數時,以上方案將失效。近年來,關于不確定參數的混沌系統的控制已引起重視。電力系統中存在著許多混沌現象。其中永磁同步電動機的數學模型是多變量、強耦合的非線性系統,能呈現出非常豐富的動態行為,如極限環和混沌。對其如何進行控制也是一個重要的研究課題。
對于不確定線性系統,基于Riccati方程和線性矩陣不等式(LMI)提出了一系列的魯棒控制器設計方法。對于不確定非線性系統,現有的研究成果還很少。實踐證明,具有線性后件的T-S模糊模型充分利用局部信息和專家經驗,能以任意精度逼近實際的控制對象。在考慮模型不確定性的情況下,文獻提出了模糊魯棒控制的概念,并取得了一定的成果。本文針對一類由T-S模糊模型表示的不確定連續非線性系統,導出了最優保代價控制器存在的充分條件。閉環系統不但漸近穩定,而且性能指標小于某一代價值。采用線性矩陣不等式(LMI)技術,給出了該控制器的設計方法和參數化表示。并將所得的控制器應用到永磁同步電動機混沌系統中,建立了永磁同步電動機混沌系統的T-S模型, 針對不包含不確定參數和包含不確定參數兩種情況,均得到了滿意的控制效果。
2 問題的描述
在系統局部信息或專家經驗存在的條件下,不確定非線性連續系統可以采用如下i條規則的T-S模糊模型進行描述:
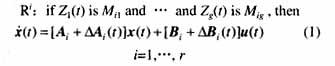
式中 Ri表示T-S模糊模型的第i條規則,也稱為模糊子系統;Z1(t),…, Zg(t)為模糊規則的前件變量;Mij為模糊語言集合;x(t)∈Rn, u(t)∈Rm分別為系統的狀態變量和控制變量;Ai, Bi是適當維數的實常數矩陣,DAi(t), DBi(t)是不確定矩陣,他們反映了系統模型中的時變參數不確定性。
本文考慮的不確定性假設是范數有界的且有如下結構:
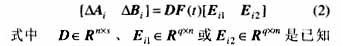
的具有適當維數的常數矩陣,它們反映了系統不確定性的結構,F(t)∈Rs×q是具有Lebesgue可測元的不確定矩陣,且滿足FT(t)F(t)≤I。
上述不確定性的結構假定并不失一般性。首先,它可以表示一個含有裝置和不確定性F(t)的線性關聯的系統;其次,有許多系統,其不確定性可以按這種方式表示,例如,滿足“匹配條件”的不確定性就可以解釋成是通過輸入進入到系統模型中的,即D為系統的輸入矩陣;最后對一般的范數有界不確定性,總可以選擇適當的結構矩陣,使其具有上面的形式。
采用文獻中的單點模糊產生器,乘積推理以及加權平均模糊消除器,上述的模糊邏輯控制系統可寫為如下形式中。
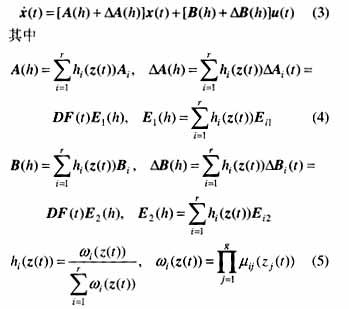


3 最優保代價控制
首先給出保代價控制的定義,然后給出模糊不確定系統(3)的穩定保代價控制器存在條件。在此基礎上利用線性矩陣不等式給出控制器的設計方法。
定義1(保代價控制)考慮不確定系統(3),如果存在控制律u*(t)和正標量J*,使得對所有允許的不確定性FT(t)F(t)≤I,閉環系統是穩定的,且代價函數(9)對此閉環系統滿足J≤J*,則稱J*是一個保代價,而稱u*(t)是不確定系統(3)的保代價控制律。
下面給出不確定系統(3)狀態反饋保代價控制律存在的一個充分條件。
定理1式(7)的反饋控制律是一個保代價控制律,如果存在公共正定矩陣P∈Rn×n和矩陣k(h),使得對任意允許的不確定性F(t),有如下矩陣不等式

設存在對稱陣P》0使得矩陣不等式(10)對所有允許的不確定性成立。定義Lyapunov函數為

因此,由Lyapunov穩定性理論,閉環模糊系統(11)是漸近穩定的。

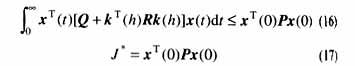
由定義1知定理1的結論成立。
下面將證明,上述推導的存在控制器使全局模糊系統漸近穩定的充分條件,可等價于線性矩陣不等式的可解性。

定理2 對于系統(11),存在對稱正定矩陣P使不等式(10)成立,當且僅當存在一標量e 》0,正定對稱矩陣X∈Rn×n和矩陣W(h)∈Rm×n滿足如下矩陣不等式
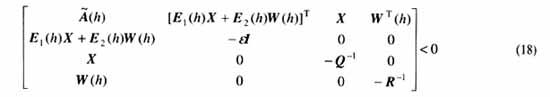

那么式(10)可被寫成式(22)

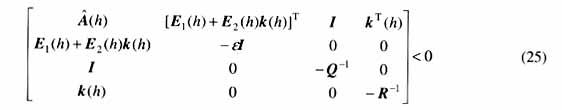
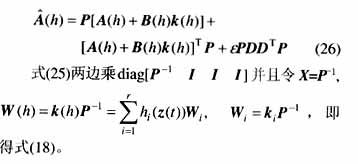
定理3 給定系統(1),存在保代價控制律(19)的條件是,存在公共正定矩陣X和矩陣Wj及標量e,滿足如下線性矩陣不等式
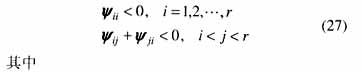
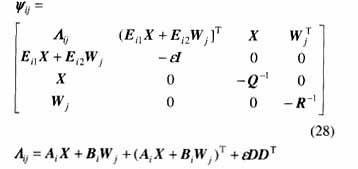
證明:由不等式(18)和式(4)可知,不等式(18)左邊等于
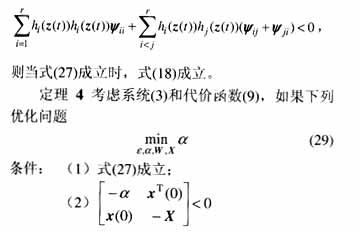
有解ε,α,W,X,則式(19)的控制律是一個無記憶狀態反饋控制律,它使得不確定系統(3)的代價函數的極小值為式(20)。
證明: 根據定理2,由任意可行解ε,α,W,X所構造的控制律(19)是系統(3)的一個保代價控制律。由Schur補引理可知,式(29)中的條件(2)等價于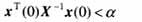
所以,由方程(20)有J*《α。
于是,極小化α隱含極小化不確定系統(3)的代價函數。而式(29)中,目標函數和約束條件的凸性,保證了該優化問題的最優性。
4 永磁同步電動機混沌系統的T-S建模與控制
4.1 T-S建模
將上述控制器應用到文獻[5-6]的永磁同步電動機混沌系統。
考慮加上一個控制項的永磁同步電動機有如下形式的數學模型(其原模型見文獻[5-6])
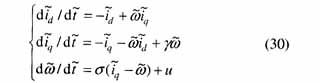
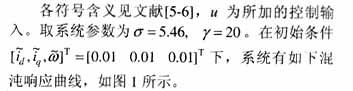
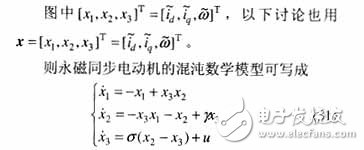
仿文獻的建模過程,對永磁同步電動機建立T-S模型。將非線性項x3(t)x2(t),x3(t)x1(t)寫成線性函數加權和的形式。
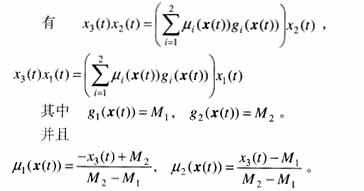
因為兩非線性項都是x3的函數,則可以構造如下精確T-S模型。
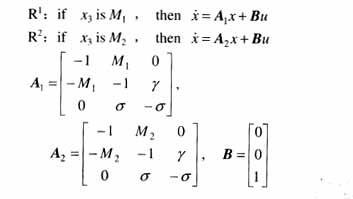
知x3(t)∈[-20,20],所以選擇M1=-20,M2=20。由推導過程可看出M1,M2是一類特殊的模糊集合,即精確的數值。是一種精確建模,無建模誤差。
4.2 系統不含不確定參數時的最優保代價控制
此時,DAi(t), DBi(t)都為0,故D,Ei1,Ei2也都為0。簡單取e=0.1,R=1,Q=I由式(27),(29)得
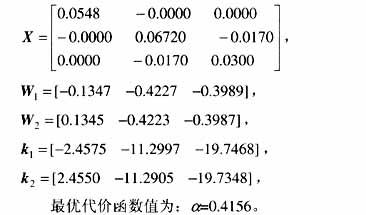
取式(7)的控制律,在初始條件為x0=(0.01 0.01 0.01)T,u=0及在t=60s加入控制項的仿真結果如圖2所示,可看出加入控制項后系統趨于穩定。
4.3 系統包含不確定參數時的最優保代價控制
假設系統參數g,s 的不確定性在其標稱值30%內。其不確定性代表參數攝動或建模誤差。在參數30%攝動下,系統仍呈現混沌行為。仿真中每個參數加30%隨機擾動,由MATLAB中的rand( )隨機函數實現,則有
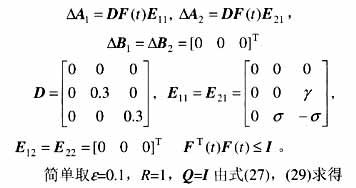
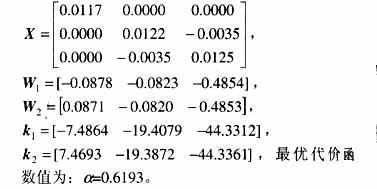
取式(7)的控制律,在初始條件為x0=(0.01 0.01 0.01)T,u=0及在t=60s加入控制項的仿真結果,可看出加入控制項后,不確定參數系統趨于穩定。
加入控制項實現了不含參數不確定性和含有參數不確定性混沌系統的穩定控制。系統狀態由原來的混沌運動迅速達到平衡點。本文的控制方法與OGY法的小信號輸入法不同,系統狀態遠離目標狀態時,啟動控制作用,即可將系統狀態控制到目標狀態,而與輸入加入的時刻無關。
5 結論
基于T-S模糊模型,給出了存在穩定最優模糊保代價控制器的充分條件和相應的LMI形式。應用到永磁同步電動機混沌系統的穩定控制中,建立了永磁同步電動機混沌系統的T-S模型,對不包含不確定參數和包含不確定參數兩種情況,取得了滿意的控制效果。不需要改變被控系統的內部結構,具有良好的穩定性,且能達到某一性能指標最優。
-
混沌控制
+關注
關注
0文章
3瀏覽量
6188 -
永磁同步電動機
+關注
關注
14文章
74瀏覽量
12048
發布評論請先 登錄
相關推薦
什么是磁阻同步電動機?它有什么特點?
一文了解同步電動機起動原理是什么
同步電動機控制策略的方法是什么?
永磁同步電動機的工作原理 永磁同步電動機的控制方法
同步電動機的起動原理 同步電動機起動的應用優勢
永磁同步電動機的工作原理 永磁同步電動機的優點有
永磁同步電動機與直流無刷電動機有何異同
同步電動機的主要結構是什么?原理有哪些?





 運用最優模糊保代價控制對永磁同步電動機混沌系統進行深度實現
運用最優模糊保代價控制對永磁同步電動機混沌系統進行深度實現












評論