引 言
2002 年美國Brown 大學David Berson 等人在哺乳動物的視網膜上發現了第三種感光細胞,它主要在調節人體內分泌、控制生理節律等非視覺生物效應方面發揮功能。照明設計也從單一地考慮視覺功能逐步過渡到考慮視覺與非視覺雙重功能上。研究表明,動態照明在治療失眠、減輕飛機時差效應、提高工作效率等方面發揮作用。
為實現LED 的動態照明設計,需對光源的光色量進行實時地控制,調制出符合光生物學要求的光譜。
這里的光色量是光度量和色度量的合稱。LED 常用的調光方法有模擬調光和PWM(Pulse Width Modulation)調光兩種。前者是線性調節LED 電流,后者是使用開關電路以相對于人眼識別力足夠高的頻率來改變光輸出的平均值。在調光過程中,防止色度量發生偏移相當重要。產生色偏的因素主要有兩個:正向導通電流和P-N 結溫度。模擬調光產生的色差取決于兩者,PWM 則主要決定于后者。一般情況下PWM 產生較小的色差(白光LED因結溫引起的色差不超過4SDCM),工程實踐中多不考慮PWM調光產生的色差。
恒流驅動下的PWM 具有以下特點:改變LED 的占空比,光度量相應地線性改變而色度量保持恒定。光度量和色度量都是整數倍于方波周期時間內的平均值。PWM 也因具有較寬的調節范圍,在工程實踐中得到了廣泛應用。
目前對PWM 調光調色的研究相對較少,此前尚缺乏一個利用PWM 同時控制光源光度量和色度量的量化計算方案。針對上述問題,提出了兩通道PWM 調光調色的混光模型,建立了期望光色量與兩通道占空比之間的一一映射。該算法能定量地調制出期望光度、色度要求的光譜,為LED 的動態照明設計提供了一個有效的實現方法。
1 方 法
1.1 兩通道PWM 調光調色的確定性
理論上可以證明,通過對LED 進行混光,兩通道PWM 的占空比與混合光的光色量之間存在確定的映射關系。這種確定性由PWM 混光技術下的幾何、光度、色度約束條件共同決定。
1.1.1 幾何約束條件
由色度學知識可知,混合光的色品坐標必在參與混光的兩光源色品坐標連線上,具體位置取決于兩種光源的混合比例。以此表示兩通道PWM 混光的幾何約束條件,用公式表示如下:

式中:xc、yc 和xw、yw 分別為參與混光的冷光源(高色溫LED)和暖光源(低色溫LED)在滿電流、占空比為100%下的色坐標;xm、ym 為混合光的色坐標。
1.1.2 光度約束條件
改變驅動LED 的PWM 占空比,其色度量不變而光度量相應地線性變化,且光度量的比值等于占空比的比值。根據測試條件,光度量可以是光通量、照度、亮度或光強,色度量可以是色品坐標或相關色溫。
若已知兩光源的占空比,則混合光的光度量可結合疊加原理計算如下:

式中:Yc、Yw 分別為參與混光的冷光源和暖光源在滿電流、占空比為100%下的光度量;Dc、Dw 分別為冷光源和暖光源的占空比;Ym 為混合光的光度量。這就是兩通道PWM 混光的光度約束條件。
1.1.3 色度約束條件
根據加混色原理及CIE1931 色坐標計算方法,占空比分別為Dc、Dw 時兩光源混光后的色坐標應滿足:

式中: Rc = Yc / yc ,Rw = Yw / yw .實際上,由幾何約束條件可知,當已知兩光源的色品坐標和混合光的x坐標時,混合光的y 坐標是確定的,且是唯一的。故兩通道PWM 混光的色度約束條件可簡化為:

1.1.4 兩通道PWM 調光調色的定量計算模型
在PWM 混光下,占空比是控制光色量的唯一因素。若期望的光度量為Ym,期望的色坐標為(xm,ym),則兩通道占空比可結合光度、色度約束條件求得。若期望的色度量是相關色溫,則需先將期望相關色溫結合幾何約束條件轉換為期望色坐標。轉換方法為:在CIE1931 色品圖中做Tm 的等溫線,把(xc,yc)和(xw,yw)的連線與此等溫線的交點作為期望色坐標(xm,ym)。聯立式(2)和式(4)并將其寫成矩陣的形式如下:
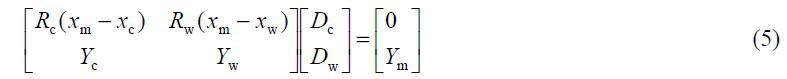
由線性代數知識可知,當 xc ≠ xw 且 yc ≠ yw 時方程組有唯一解。由此可知,給定期望色度、光度值下的占空比是確定的,且是唯一的。此時,計算占空比與計算混合光的光色量是可逆過程。
1.2 兩通道PWM 調光調色的局限性
理論上,混合光色坐標xm 的取值范圍為[xc,xw](設 xc < x w),混合光的光度量 Ym 的取值范圍為[0, Yc + Y w ].混合光色度量和光度量所有可能取值所圍成的區域稱作理論域。事實上,兩通道PWM 的調光調色方法并不能實現理論域中的所有取值,而僅可實現部分特定的區域。可實現的區域稱作可行域,可行域的邊界主要由電力約束條件決定。
1.2.1 電力約束條件
從實際意義出發,兩通道的占空比還應滿足0≤ Dc ≤1 ,0 ≤ Dw ≤1 ,將式(5)解得的Dc、Dw代入該不等式,經化簡后得到兩通道PWM 混光下的電力約束條件如下:

上述電力約束條件可由圖1 表示,圖中x0=(Rc xc+ Rwxw ) /(Rc +Rw),是兩種LED占空比之比為1:1 時混合光的色坐標x.圖中所示的整個矩形區域就是兩通道PWM 混光下的理論域,陰影部分即為可行域。若參與混光的兩種LED 已選定,當利用式(5)計算實現期望光色量的占空比時,應首先判斷期望值是否在可行域內。若在可行域中,則可利用兩通道PWM 混光方法得到。
否則,應考慮更換參與混光的光源。
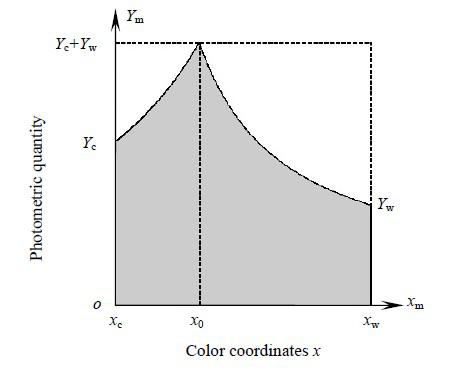
圖1 兩通道 PWM 調光調色的理論域和可行域
1.2.2 局限性的表征
為表征兩通道PWM 調光調色的能力,定義可控比,它是可行域與理論域的比值,用公式表示為:
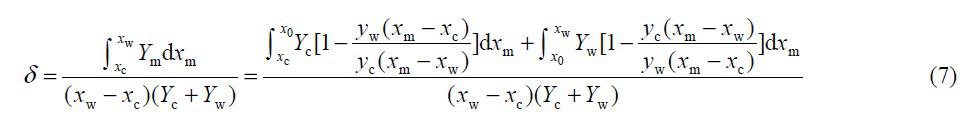
式中:δ 為可控比。將式(7)化簡后可得:
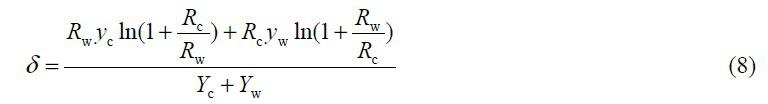
從上式可以看出,可控比由參與混光的兩光源本身決定,與外在控制方法無關。可控比越大,說明PWM調控裕度越大,實現預期光度、色度值的概率越大。所以,可控比可作為光源組合選擇優劣的評判標準。
從圖1 中還可以看出:1) 混合光的色度量能且僅能在對應于x0 處取遍所有理論光度值;2) 若混合光的光度量不大于Yc、Yw 中的較小者,則可取遍所有理論色度值。所以要實現所有的色度值,Yc 和Yw 不應相差太大,且兩者的較小值應與期望光度值中的最大值相當。同樣實驗表明,Rc 和Rw 的差值越小,則可控比就越大,兩種LED 的利用率就越高。所以,在都能實現期望值的情況下,應選擇Rc 和Rw 相差最小的光源組合。
2 實驗與結果分析
根據P.R. Boyce、J.W. Beckstead、N.H. Eklund 等人實驗提供的日光照度和色溫變化曲線,選取26個時間關節點上的光色值,對從黎明到中午的自然光進行模擬。根據光色值的變化范圍,選擇了兩種高顯色性白光LED,LED 的光色電等基本參數如表1 所示。
根據兩通道PWM 調光調色的局限性,計算期望光色值在理論域中的坐標值,如圖2 所示。進而根據式(5)計算落在可行域內的各光色值的占空比。單片機把各時間點具備特定占空比的方波動態分配給相應的LED 驅動芯片。兩種LED 均勻分布并用乳白玻璃將燈光混合,用檢測設備實時測量其混合光的光色量。
檢測儀器選用SUV3000 紫外可見光譜輻射分析儀,測量過程在標準暗室中進行。測量結果如圖3 所示。
實測照度值與期望照度值的平均誤差為15 lx,實測色溫值與期望色溫值平均誤差為23 K.
表1 實驗用 LED 的基本參數

實驗過程中,實測值與理論值存在一定的誤差,但總體上還是得到了很好的匹配。誤差主要來自以下幾個方面:1) 隨著實驗過程的進行,LED 芯片的結溫不斷升高。結溫的改變會引起其光度量和色度量的變化。2) 驅動LED 芯片的PWM 波形并非理想的方波。即使在同一開關狀態下,電流也并非保持恒定。
而驅動電流的變化則會導致LED 光度量和色度量的變化。占空比越小,這種情況引起的誤差就越大。
3) LED 個體性差異。即使是同一型號,同一批次的LED,其光度量和色度量也會不同,特別是兩者的動態特性。而在實驗中認為同一種LED 具有相同的光色電參數和動態特性。4) 檢測儀器的系統誤差以及操作過程中的隨機誤差。
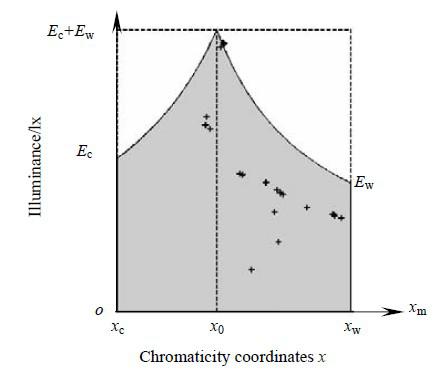
圖2 實驗光色值在理論域中的分布。
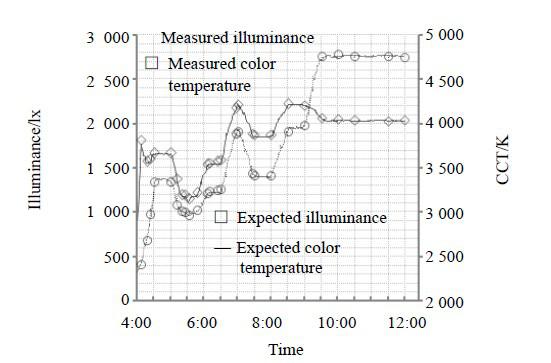
圖 3 模擬從黎明到中午自然光的照度和色溫變化。
3 結 論
本研究提出了一種新型的基于PWM 的調光調色方法,建立了關于期望光色量和兩通道占空比的一一映射模型,可以準確的實現預期光度和色度要求的光譜,為LED 的動態照明技術提供了理論依據和實現方法。另外,該調光調色方法在LED 背光領域亦具有潛在的應用前景。
-
led
+關注
關注
242文章
23153瀏覽量
658614 -
照明
+關注
關注
11文章
1507瀏覽量
131273 -
PWM
+關注
關注
114文章
5153瀏覽量
213447
發布評論請先 登錄
相關推薦




 通過兩通道PWM混光技術實現LED的調光調色方法
通過兩通道PWM混光技術實現LED的調光調色方法

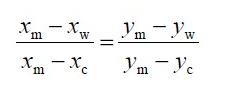













評論