信息工程監理，就是監理服務商依照有關技術標準與規范、法律法規、業主需求以及業主與承建方簽定的合同，本著科學、公正、嚴格、守信、遵紀、守法的原則，以高度的責任心、豐富的管理經驗和專業技術能力，幫助業主審核建設承包合同條款、掌控工程進度和質量、進行成本核算，按期分段對工程進行驗收，對工程建設項目實施全面而有重點的、精線條的監督管理，保證工程高質量地、按期完成，最終提交業主滿意的成果。因此，信息工程監理的宗旨，就是協助業主進行項目管理，幫助業主防范工程建設中可能出現的各種風險，最終維護業主的合理利益。本文通過對信息工程質量監理過程特點的分析，將隱馬爾可夫模型映射到質量監理中，利用前向算法估計出在該模型下觀測事件序列發生的概率，從而在一定程度上有助于對軟件質量進行定量控制。

1 模型的建立

1.1 特征提取

隱馬爾可夫模型（Hidden Markov Model,HMM）作為一種統計分析模型，創立于20世紀70年代。80年代得到了傳播和發展，成為信號處理的一個重要方向，現已成功地用于語音識別，行為識別，文字識別以及故障診斷等領域。隱馬爾可夫模型是馬爾可夫鏈的一種，它的狀態不能直接觀察到，但能通過觀測向量序列觀察到，每個觀測向量都是通過某些概率密度分布表現為各種狀態，每一個觀測向量是由一個具有相應概率密度分布的狀態序列產生。所以，隱馬爾可夫模型是一個雙重隨機過程----具有一定狀態數的隱馬爾可夫鏈和顯示隨機函數集。自20世紀80年代以來，HMM被應用于語音識別，取得重大成功。到了90年代，HMM還被引入計算機文字識別和移動通信核心技術"多用戶的檢測".近年來，HMM在生物信息科學、故障診斷等領域也開始得到應用。

將隱馬爾可夫模型映射到信息工程監理質量評估模型上，即一個軟件的質量狀態是無法直接觀察到的，但是可以通過分析與這個軟件相關的質量度量要素，估算該軟件的質量狀態，從而進一步得到其量化的評判值。信息化工程監理國標中的信息化工程監理規范技術參考模型，將信息工程質量監理分為工程招標、工程設計、工程實施和工程驗收四個階段。各個階段的軟件質量狀態構成一個馬爾可夫鏈，度量要素序列是一個隨機過程，每一個度量要素會對軟件的質量狀態的轉移帶來一定影響，這樣，度量要素序列和軟件的質量狀態之間就構成了一個隱馬爾可夫模型。通過觀察信息工程監理全過程各個階段的度量要素，每個階段都可以得到一個隨機的度量要素序列，這樣就可以計算軟件的質量狀態和評判值。

軟件質量目標控制按照分層法分解為人、軟件元、開發方法、設備及材料和工程環境五個度量要素，軟件質量狀態依據各度量要素分為優、良、中、差四個決斷因子，如果再定義出它們之間的概率轉換關系，就會得到由這兩組狀態構成的隱馬爾可夫模型（如圖1所示）。

根據該HMM模型，可以在沒有直接觀測軟件質量的情況下根據度量要素的分布來推測軟件質量的變化情況。

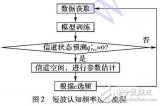
如果能較為準確地計算軟件質量處于何種狀態，則可以定量分析軟件的質量情況。軟件質量狀態之間的轉移見圖2.

由圖1可以直觀看出，度量軟件質量的要素有5個，用V={P,U,M,F,E}表示，ν1=P（People），表示度量要素人的因素；ν2=U（Units），表示度量要素軟件元質量；ν3=M（Methods），表示度量要素開發方法；ν4=F（Facilities），表示度量要素設備及材料；ν5=E（Environment），表示度量要素工程環境。設質量度量要素觀測序列為O={o1,o2,o3,o4},其中ot∈V.

設軟件質量情況在信息工程監理開始階段狀態為π，它是一個向量，表示在信息工程監理工程招標階段軟件質量處于各個狀態的概率，π={π1,π2,π3,π4},πi=P（q1=si），1≤i≤4.對于工程招標階段，可以根據信息工程監理協同工作平臺下的模糊因素神經網絡質量評估方法得到一個默認值，之后的每一階段，通過Trans和Obs可以計算出當前軟件質量處于各種狀態的概率st=（r1,…，r4），將此概率作為下一階段的初始狀態。在t階段，狀態分布表示為rt={rt（i）},1≤i≤4,狀態的分布概率公式為：rt（i）=P（qt=si|λ）。再引入一個代價向量C[10],代表軟件在每個狀態的質量值，則可以將軟件狀態的定性分析轉化為定量分析。

設Trans為軟件質量狀態轉換矩陣，即質量狀態之間轉換的概率組成的矩陣，包含4行4列，aij表示在t階段質量狀態為si,那么到t+1階段質量狀態為sj的概率，即aij=P（qt+1=sj|qt=si），1≤i,j≤4.

定義Obs為當軟件處于某一個特定質量狀態時觀測到某種度量要素的概率矩陣，bj（k）表示在階段t,軟件質量處于sj狀態觀測到度量要素νk的概率，1≤k≤5,1≤j≤4.

2 基于前向算法的模型應用

根據得到的觀察序列O={o1,o2,o3,o4}和模型λ=（π，Trans,Obs）可以計算出在該模型下觀察事件序列發生的概率P（O|λ）。P（O|λ）評價了給定模型？姿與給定觀測序列匹配的程度。

對隱馬爾可夫模型而言，狀態轉換序列是隱藏的，一個觀測序列可能由任何一種狀態轉換序列產生。因此要計算一個觀測序列的概率值，就必須考慮所有可能的狀態轉換序列。

窮舉搜索的時間復雜度是2TNT,前向算法的時間復雜度是2N2T,其中T指的是觀察序列長度，N指的是隱藏狀態數目。對于信息工程監理質量控制，N=4,T=4,如果利用窮舉搜索算法，復雜度相對會比較大，可以采用前向算法來降低復雜度。

給定這種算法，對于已知的一個度量要素觀察序列，可以直接用來確定在一些隱馬爾可夫模型中哪一個最好地描述了它，即先用前向算法評估某一個給定的λ，然后通過多次調整參數λ來提高評估的概率，進而通過實時調整信息工程監理中的質量的度量要素的比例來達到提高軟件質量控制的目的。

3 仿真實驗

實驗數據于信息工程監理協同工作平臺（IPSS）下的數據庫。實驗環境為Eclipse和Java開源工具包jahmm-0.6.1.文中使用狀態數為N=4,觀測值數為M=5的隱馬爾可夫模型進行檢驗。

在信息工程監理中，每個階段軟件所處的質量狀態與前一階段所處的質量狀態有關，即前一階段的質量狀態會影響下一階段質量狀態出現的概率。

初始質量狀態概率分布：π=（0.3,0.3,0.2,0.2）

四個質量狀態兩兩之間轉化的概率如表1所示。

軟件質量處于某個狀態時，度量要素所占的比例有一定的規律性。度量要素觀測值概率分布如表2。

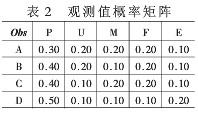
下面根據軟件質量初始狀態、表1和表2的數據，估計狀態序列O={P,U,M,F}出現的概率。假設P為工程招標階段觀測到的主導要素，U為工程設計階段觀測到的主導要素，M為工程實施階段觀測到的主導要素，F為工程驗收階段觀測到的主導要素。

在模型λ下，在t時刻觀測事件是ot、狀態是si的概率如表3所示，每個階段的四個概率對應四個質量狀態。

本文通過對隱馬爾可夫理論的分析，建立了用于質量控制的隱馬爾可夫模型，并嘗試基于該模型對信息工程監理進行質量控制。本文提出的隱馬爾可夫質量控制模型只是用于控制信息工程監理4個階段的5個基本要素，模型稍顯粗糙。如何基于隱馬爾可夫模型或其他擴展模型與信息工程監理質量控制完全的整合，以及如何利用模型進行質量評估并對模型進行訓練還需要進一步的探索研究。