1.引言

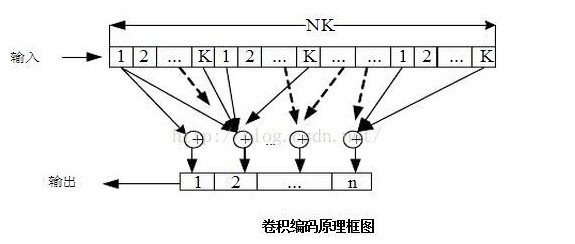
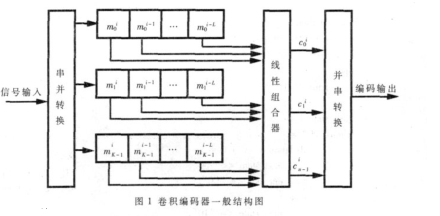
卷積碼的編碼器是由一個有k位輸入、n位輸出，且具有m位移位寄存器構成的有限狀態的有記憶系統，通常稱它為時序網絡。編碼器的整體約束長度為v,是所有k個移位寄存器的長度之和。具有這樣的編碼器的卷積碼稱作[n,k,v]卷積碼。對于一個（n,1,v）編碼器，約束長度v等于存儲級數m.卷積碼是由k個信息比特編碼成n（n>k）比特的碼組，編碼出的n比特碼組值不僅與當前碼字中的k個信息比特值有關，而且與其前面v個碼組中的v*k個信息比特值有關。

卷積碼有三種譯碼方式：序列譯碼、門限譯碼和概率譯碼。其中，概率譯碼根據最大似然譯碼原理在所有可能路徑中求取與接收路徑最相似的一條路徑，具有最佳的糾錯性能，維特比譯碼是概率譯碼中極重要的一種方式。

序列譯碼和門限譯碼則不一定能找出與接收路徑最相似的一條路徑。不同于維特比譯碼，門限譯碼與序列譯碼所需的計算量是可變的且對于給定信息分組的最終判決僅僅基于（m+1）個接收分組，而不是基于整個接收序列。

與維特比譯碼所使用的對數似然量度不同，序列譯碼所使用的量度為Fano量度。在接收序列受擾嚴重的情況下，序列譯碼的計算量大于維特比譯碼所需的固定計算量，雖然序列譯碼要求的平均計算次數通常小于維特比譯碼。在采用并行處理的情況下，維特比譯碼的速度會優于序列譯碼。在同樣碼率和存儲級數的條件下，門限譯碼的性能比維特比譯碼低大約3dB.

維特比譯碼的數據輸出方式有硬判決及軟判決兩種方式，本文選取生成多項式為561,753的（2,1,8）卷積碼對硬判決的性能進行分析，并依據維特比譯碼的原理以及卷積碼的特性，對卷積碼編碼和維特比譯碼過程在加性高斯白噪聲（AWGN）信道下進行仿真，并且根據仿真結果對維特比譯碼（硬判決）的結果進行分析。由于卷積碼的生成可以看做一個馬爾科夫過程，因此，不同狀態間的轉移概率對描述這個過程有極關鍵的作用。本文則基于MATLAB對不同狀態間的轉移概率進行求解，從而更準確地分析維特比譯碼的性能。仿真結果表明卷積碼抗突發錯誤的能力不強，生成多項式為561,753的（2,1,8）卷積碼在信噪比大于1dB時，編碼增益體現明顯。在信噪比低于-1dB時，編碼增益得不到體現。

2.卷積碼編碼譯碼原理

卷積碼編碼通過輸入序列與生成多項式的每一行做卷積，每次輸入k比特，輸出n個比特。在卷積碼編碼器中，每（m+1）個比特構成譯碼器中的一個狀態。假設在一個二進制輸入的離散無記憶信道上，有一個長度為k*L的信息序列u=（u0,u1,…，uL-1）被編碼成為長為T=n（L+m）的碼字c=（c0,c1,…，cT-1），接收到的序列為r=（r0,r1,…，rT-1）。維特比譯碼使用對數量度來衡量幸存路徑所編成的碼字與接收序列的相似度，量度越大，說明該幸存路徑是信息序列的概率越大。維特比譯碼選取那條量度最大的幸存路徑作為譯碼結果。

由于對離散無記憶信道：

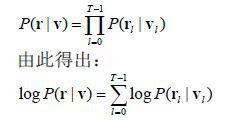
其中P （ r l | v l ）是信道轉移概率；logP（r|v）稱為和路徑v相關的量度，以M（r|v）表示；logP（rl|vl）稱為分支量度。

維特比譯碼的原理則是找出一條路徑，使得該路徑的累積量度最大。在譯碼過程中，如果在某一節點上發現某路徑已不可能是需要找到的那條路徑，就將此路徑去掉，不保存在幸存路徑之中。然后再在剩下的幸存路徑中選擇譯碼路徑，直到輸入所有譯碼器序列。理論上，搜索路徑需要無限長度，而實際應用中考慮到試驗因素搜索長度有限，搜索長度對譯碼性能有一定的影響，搜索路徑的長度一般為約束長度的四倍到五倍。維特比譯碼可以被總結成如下步驟：

第一步：在時間單元t=m開始，計算進入每一狀態的單個路徑的部分量度，并存儲每一狀態下的路徑（幸存的）及其量度。

第二步：t增加1.將進入每一狀態的分支量度與前一時間單元有關的幸存路徑的量度相加，計算進入該狀態的所有2k路徑的部分量度；對每一狀態，比較進入該狀態的所有2k路徑的量度，選擇具有最大量度的路徑（幸存路徑），存儲該路徑及其量度，并刪除其他所有路徑。

第三步： 如果t < L + m , 重復步驟二；否則停止。

維特比譯碼性能分析：

假設一個二進制序列經BPSK調制后通過加性高斯白噪聲（AWGN）信道后的誤比特率為e,因為本文采用的生成多項式為561,753的（2,1,8）卷積碼編碼器，則有9*2=18個比特與當前輸出比特相關。由于該卷積碼的自由距為12,因此如果一個比特出現譯碼錯誤，則留下的幸存路徑（也即最大似然路徑）經編碼后的序列會與正確路徑的序列相差1 2比特，并且會對其后18個比特產生影響。

所以，維特比譯碼抗突發錯誤能力不強，而實際應用時往往在卷積編碼后加入交織編碼，使突發錯誤離散化。因為卷積碼的馬爾科夫性，可以推測出：當不編碼時，若誤比特率足夠高，則編碼后序列的誤比特率會比不編碼更高。而仿真結果表明，當未編碼序列的誤比特率達到8*10-2,隨著未編碼序列的誤比特率升高，編碼后序列的誤比特率會迅速升高。而在當未編碼序列的誤比特率小于5*10-2時，編碼后序列的誤比特率升高得較為緩慢且編碼增益得到明顯體現。

3.卷積碼編碼及維特比譯碼仿真

自編函數對維特比譯碼仿真：

本文應用MATLAB對卷積碼編碼器以及維特比譯碼器進行仿真。由于卷積碼的馬爾科夫性，轉移概率是其中一個重要特性。顯然，如果其中一個比特譯碼錯誤，后面N個比特的誤比特率都會因此受到影響，所以需要求出一步轉移概率、兩步轉移概率…N步轉移概率。由于本文采用的是（2,1,8）卷積碼，N=8.

基于MATLAB首先編寫出模擬卷積碼編碼和維特比譯碼的函數，再分類討論。在一定誤比特率情況下，當影響第L個比特譯碼的2*9個比特中錯n（n=1,2,3…，18）個時，求得第（L+N）比特譯碼錯誤的轉移概率。假設BPSK調制的誤碼率為e;在影響第L比特譯碼結果的18個比特中有n個誤比特時，假設第（L+h）個比特經譯碼后的誤比特率為P （h） n .

由于加性高斯白噪聲信道是非記憶信道，則譯碼后序列的誤比特率近似等于：

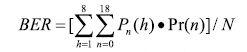
其中Pr（n）是18個比特中有n比特錯的概率，當誤比特率為e, ,N=18.

創建m文件，函數有三個輸入：生成多項式G、接收到的信道輸出誤比特率BER、影響第x比特譯碼結果的18比特中的誤比特數n,輸出則是P （h） n .這里h的值為1~8.對于信道輸出序列的誤碼率為0.1時進行分析，基于MATLAB仿真得到的所有P （h） n 如圖1所示。

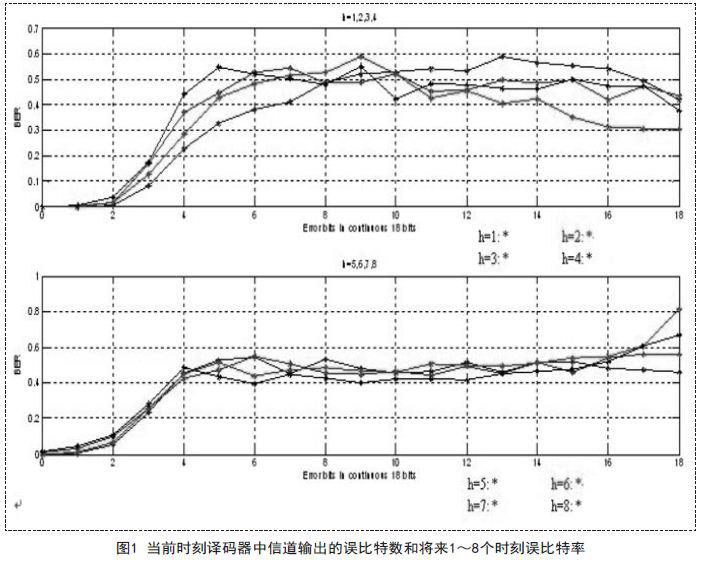
由圖1中的結果可以算出當接收到的信道輸出序列的誤碼率為0.1時，經維特比譯碼后的誤比特率約為0.1071.

而且，當信道輸出中連續1 8比特的誤比特數大于3 時， 第（ x + h ） 個比特的誤比特率遠高于平均誤比特率，這表明維特比譯碼抗突發錯誤能力低下。

以n=4為例，根據圖1中數據可得出當h=1,2,…，8時，第（x+h）個比特的平均誤比特率為0 . 3 9 2 2.當n的值比較小時（ n < 4 ），可以得到以下結論，當h=1,2,…，8時，第（x+h）個比特的誤比特率隨h增加而增大。由于卷積碼的特性，第L個比特的譯碼結果可直接影響第（x+j）個比特（j=1,2,…，7）的譯碼結果，而第（x+j）個比特的譯碼結果又會直接影響第（x+h）個比特（h=1,2,…，8）的譯碼結果。因為這種迭代關系，第（x+h）個比特的誤碼率會隨h增大而增大，從而造成卷積碼抗突發錯誤性能低下。并且，在信道輸出的誤碼率較大時，碼字速率已經大于信道容量，此時采用編碼不可能進行可靠通信。

仿真結果表明：當信噪比等于-1dB時，一個序列通過加性高斯白噪聲信道后接收到的信道輸出誤比特率大于10-1,且該序列運用[2,1,8]卷積碼編碼，維特比譯碼（硬判決）后所得的序列誤比特率升高。當信噪比為2dB時，一個序列通過加性高斯白噪聲信道后接收到的信道輸出誤比特率約為4*10-2,且該序列運用[2,1,8]卷積碼編碼，維特比譯碼后所得的序列誤比特率小于10-3,誤碼率遠低于不編碼時的誤碼率。因此卷積碼適用于信道輸出誤碼率比較低時候。

4.結論

本文基于MATLAB對卷積碼編碼和維特比譯碼進行仿真，比較了未編碼序列的誤比特率和編碼后序列的誤比特率。依據卷積碼的馬爾科夫性，利用MATLAB仿真，對其轉移概率進行了求解，并通過轉移概率得出了維特比譯碼的性能以及卷積碼抗突發錯誤能力不高的結論。當信噪比為-1dB時，生成多項式為561,753的（2,1,8）卷積碼的誤碼率約為1.27*10-1,而不編碼的BPSK的誤碼率約為1.04*10-1,編碼后誤碼率反而高于不編碼。在信道條件較好時，卷積碼的編碼增益體現明顯，當信噪比為2dB,生成多項式為561,753的（2,1,8）卷積碼的誤碼率約為8*10-4,而不編碼的BPSK的誤碼率約為4.64*10-2,編碼后誤碼率明顯降低。