1 、引 言
隨機(jī)序列是一組滿足特定統(tǒng)計(jì)學(xué)規(guī)律的數(shù)據(jù),在信號(hào)理論分析中應(yīng)用非常普遍。由于 精確的隨機(jī)序列生成方法較為復(fù)雜,產(chǎn)生的隨機(jī)序列不具有可重復(fù)性等特點(diǎn),在很多應(yīng)用 場合使用偽隨機(jī)序列。偽隨機(jī)序列在擴(kuò)頻通信、信息加密和系統(tǒng)測試等諸多領(lǐng)域中都有著 廣泛的應(yīng)用。在自適應(yīng)光學(xué)SPGD 算法中,偽隨機(jī)序列亦有相當(dāng)重要的作用。
Vorontsov 等人在1997 年將SPGD 算法引入到自適應(yīng)光學(xué)領(lǐng)域。國內(nèi)在近幾年開始了對(duì) SPGD 算法在自適應(yīng)光學(xué)系統(tǒng)應(yīng)用的研究,并且在計(jì)算機(jī)上用軟件編程實(shí)現(xiàn)了算法,進(jìn)行 了自適應(yīng)光學(xué)的系統(tǒng)實(shí)驗(yàn)。自適應(yīng)光學(xué)SPGD 控制算法的研究趨勢是使用專用的信號(hào)處 理硬件電路作為算法的實(shí)現(xiàn)平臺(tái),以獲得更高的迭代速度和更好的收斂效果。Cauwenberghs等人設(shè)計(jì)了專用的模擬超大規(guī)模集成電路實(shí)現(xiàn)SPGD 控制算法,并且在一些應(yīng)用領(lǐng)域進(jìn)行 了實(shí)驗(yàn)。目前自適應(yīng)光學(xué)系統(tǒng)的規(guī)模普遍達(dá)到幾十上百單元。針對(duì)多單元自適應(yīng)光學(xué)系 統(tǒng)SPGD 控制算法的特殊要求,本文提出了一種適合于用FPGA 硬件電路產(chǎn)生滿足算法要 求的多路偽隨機(jī)序列的生成方法,完成了FPGA 電路的硬件實(shí)現(xiàn),并將其用于實(shí)現(xiàn)61 單 元自適應(yīng)光學(xué)SPGD 控制算法,同時(shí)進(jìn)行自適應(yīng)光學(xué)的閉環(huán)實(shí)驗(yàn)。
2 、自適應(yīng)光學(xué) SPGD 控制算法對(duì)偽隨機(jī)序列的要求
SPGD(the Stochastic Parallel Gradient Descent algorithm)算法通過對(duì)多路的控制參數(shù)加 入隨機(jī)并行的擾動(dòng),使用性能指標(biāo)測量值的變化量與控制參數(shù)的變化量進(jìn)行控制參數(shù)的梯 度估計(jì),以迭代方式在梯度下降方向上進(jìn)行控制參數(shù)的搜索。在自適應(yīng)光學(xué)SPGD 算法中, 控制參數(shù)為變形鏡的控制電壓,隨機(jī)并行的擾動(dòng)通過多路偽隨機(jī)序列模擬。SPGD 算法中 隨機(jī)并行擾動(dòng)的特性,對(duì)偽隨機(jī)序列也提出了相應(yīng)的要求:
(1) 路數(shù)多。路數(shù)等于變形鏡單元數(shù)(即變形鏡上驅(qū)動(dòng)單元的數(shù)目)。例如在一個(gè)61 單 元的自適應(yīng)光學(xué)系統(tǒng)中,就需要產(chǎn)生61 路的偽隨機(jī)序列。
(2) 偽隨機(jī)序列兩兩相互獨(dú)立。相互獨(dú)立可避免變形鏡各驅(qū)動(dòng)單元間的相互耦合。
(3) 偽隨機(jī)序列符合伯努利分布,兩個(gè)樣本值出現(xiàn)的概率各為0.5。
3 、硬件電路實(shí)現(xiàn)偽隨機(jī)序列的傳統(tǒng)方法
傳統(tǒng)的生成偽隨機(jī)序列的方法較多,如線性反饋移位寄存器法(LFSR,可產(chǎn)生M 序列), 乘同余法,線性同余法,Gold 序列等。M 序列是一種常用的隨機(jī)序列,符合SPGD 算 法中單路隨機(jī)序列伯努利分布的要求。但使用M 序列作為SPGD 算法中多路隨機(jī)序列在實(shí) 現(xiàn)上存在難點(diǎn):算法要求多路偽隨機(jī)序列,用多個(gè)不同的LFSR 結(jié)構(gòu)去生成多路的偽隨機(jī) 序列,需要耗費(fèi)大量的硬件資源,并且構(gòu)造多路不同的LFSR 結(jié)構(gòu)需耗費(fèi)巨大的工作量。
Gold 序列優(yōu)點(diǎn)在于只由兩個(gè)M 序列構(gòu)造,能夠節(jié)省資源;并且改變兩個(gè)M 序列模二 和的相對(duì)位置即可構(gòu)成多個(gè)Gold 序列,從而滿足SPGD 算法中多路偽隨機(jī)序列的要求。 但在實(shí)際工程中如何方便改變兩個(gè)M 序列的相對(duì)位置以產(chǎn)生多路的Gold 序列亦有難度。 同時(shí),Gold 序列亦存在非平衡性問題,不完符合伯努利分布。
國外最早使用模擬超大規(guī)模集成電路(Analog VLSI)做出SPGD 控制算法的Vorontsov 等人設(shè)計(jì)的隨機(jī)數(shù)發(fā)生器,其本質(zhì)也是LFSR 結(jié)構(gòu),使用了抽頭的方法從而可以用一個(gè) LFSR 結(jié)構(gòu)同時(shí)產(chǎn)生19 路的偽隨機(jī)序列。這種方法的缺陷是如果偽隨機(jī)序列的路數(shù)序 列超過19 路后,則用這個(gè)電路結(jié)構(gòu)產(chǎn)生的各路偽隨機(jī)數(shù)之間不是完全相互獨(dú)立的。
4 、連續(xù)抽樣生成多路偽隨機(jī)序列的方法
通過以上對(duì)M 序列,Gold 序列的分析,結(jié)合M 序列易于硬件實(shí)現(xiàn),Gold 序列可生成 多路序列的優(yōu)點(diǎn),以及基于時(shí)間抽樣的思想,設(shè)計(jì)了如圖1 所示硬件結(jié)構(gòu)的68 路偽隨機(jī) Gold 序列發(fā)生器。
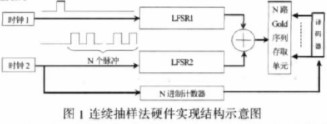
圖中所示結(jié)構(gòu)包括兩個(gè)時(shí)鐘,兩個(gè)相同的線性反饋移位寄存器,N 進(jìn)制計(jì)數(shù)器,以及N 路偽隨機(jī)序列的存取單元。兩個(gè)時(shí)鐘有特殊的關(guān)系,即時(shí)鐘1 是時(shí)鐘2 的N 分頻。N 進(jìn) 制計(jì)數(shù)器的輸出作為N 路偽隨機(jī)序列存取單元的存儲(chǔ)地址。存取單元及地址譯碼器可視為 一個(gè)整體,在實(shí)現(xiàn)時(shí)使用深度為N,寬度為1bit 的雙端口RAM 代替(一個(gè)端口存數(shù)據(jù), 另一個(gè)端口取數(shù)據(jù))。此外,圖中的“+”表示模二和。結(jié)構(gòu)中的N 值,為本原抽樣數(shù), 即使用N 對(duì)M 序列抽樣后,可得到另一同周期的M 序列。
上述結(jié)構(gòu)產(chǎn)生多路Gold 序列的原理如下:

該方法需要選定兩個(gè)可構(gòu)成Gold 序列的理想M 序列對(duì),之后將能夠從一個(gè)M 序列抽 樣出另一M 序列的本原抽樣數(shù)N 預(yù)先計(jì)算出來。由于是預(yù)先計(jì)算,不需在硬件內(nèi)實(shí)現(xiàn), 不占用硬件資源。因此該方法占用的資源較少,同時(shí)結(jié)構(gòu)化的設(shè)計(jì)也適合于用硬件描述語 言進(jìn)行設(shè)計(jì)。
5 、實(shí)驗(yàn)及結(jié)果分析
為驗(yàn)證上述偽隨機(jī)序列生成方法的可行性,在FPGA 內(nèi)對(duì)上述結(jié)構(gòu)進(jìn)行了硬件設(shè)計(jì), 并搭建了基于SPGD 控制算法的自適應(yīng)光學(xué)系統(tǒng)平臺(tái)。自適應(yīng)光學(xué)系統(tǒng)實(shí)驗(yàn)平臺(tái)的結(jié)構(gòu)如 下圖3 所示,主要由激光器和擴(kuò)束系統(tǒng)、傾斜鏡TM、變形鏡DM、CCD 相機(jī)、基于FPGA 的SPGD 算法控制處理器、數(shù)字到模擬轉(zhuǎn)換器DAC 和高壓放大器HVA 等組成。光源從激 光器發(fā)出后經(jīng)TM 和DM 反射至CCD 相機(jī),相機(jī)將圖像數(shù)據(jù)傳輸給FPGA 板進(jìn)行算法迭 代,再輸出電壓至數(shù)模轉(zhuǎn)換,最后經(jīng)高壓放大后控制61 單元的變形鏡DM(驅(qū)動(dòng)器的排布 見圖(3)和傾斜鏡TM,完成閉環(huán)控制。
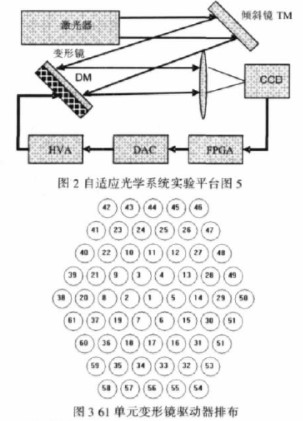

SPGD 算法包括偽隨機(jī)序列發(fā)生器都在Xilinx 公司的VII3000 FPGA 內(nèi)實(shí)現(xiàn)。通過 ChipScope 在線邏輯分析儀記錄68 路Gold 序列,經(jīng)計(jì)算驗(yàn)證這68 路Gold 滿足相互獨(dú)立 的要求。針對(duì)Gold 序列的非平衡性問題,根據(jù)序列的周期性及對(duì)偶性,實(shí)驗(yàn)運(yùn)用了一個(gè)簡 單的方法加以解決:將偶數(shù)周期的兩個(gè)樣本值互相交換,即應(yīng)該輸出1 時(shí)輸出0,應(yīng)該輸 出0 時(shí)輸出1。因此每兩個(gè)周期內(nèi)的兩個(gè)樣本值出現(xiàn)的概率各為0.5,只要序列發(fā)生的時(shí)間 足夠長,長期統(tǒng)計(jì)平均,其概率亦各為0.5。因此通過實(shí)驗(yàn)驗(yàn)證表明連續(xù)抽樣方法能夠滿足 自適應(yīng)光學(xué)SPGD 算法的要求。
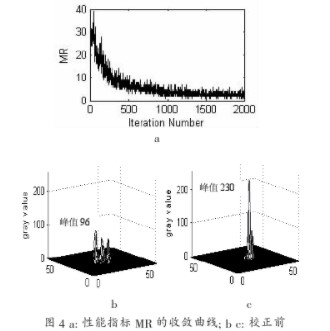
自適應(yīng)光學(xué)系統(tǒng)實(shí)驗(yàn)方面,以均值半徑作為本實(shí)驗(yàn)中SPGD 算法的性能指標(biāo),向極 小的方向進(jìn)行梯度搜索,性能指標(biāo)的收斂曲線如圖4(a)所示。在迭代1000 次后,曲線就已 接近極小值。圖4(b)和7(c)是進(jìn)行校正前后,CCD 相機(jī)中獲取的遠(yuǎn)場光斑的光強(qiáng)分布圖。 校正前的峰值為96,校正后的峰值為230,校正后的遠(yuǎn)場光斑接近艾里斑,結(jié)果說明使用 SPGD 算法對(duì)靜態(tài)的波前畸變達(dá)到了良好的效果,同時(shí)也驗(yàn)證了本方法所產(chǎn)生的偽隨機(jī)序 列能夠在實(shí)際的SPGD 控制算法中正常工作。
6 、結(jié)論
利用FPGA硬件電路生成了61單元自適應(yīng)光學(xué)系統(tǒng)SPGD控制算法要求的68路偽隨機(jī)序列。開展了基于SPGD控制算法自適應(yīng)光學(xué)系統(tǒng)實(shí)驗(yàn),系統(tǒng)能夠?qū)崟r(shí)閉環(huán),結(jié)果表明了該方 法的實(shí)用性。同時(shí),該方法除了滿足自適應(yīng)光學(xué)系統(tǒng)SPGD控制算法的專用性外,也為生成 大量的、任意多路的偽隨機(jī)序列提供了一種通用的方法,在信號(hào)處理、信號(hào)加密等工程領(lǐng)域 也具有一定的實(shí)際意義。
針對(duì)自適應(yīng)光學(xué)系統(tǒng)的SPGD 控制算法對(duì)偽隨機(jī)序列的要求,分析 了兩種適合于硬件實(shí)現(xiàn)的偽隨機(jī)序列――M 序列及Gold 序列的特點(diǎn),及直接用于SPGD 控制算法存在的問題。在M 序列抽樣方法的基礎(chǔ)上,提出了一種連續(xù)抽樣生成多路Gold 序列的方法。該方法在對(duì)時(shí)間未要求的基礎(chǔ)上,以時(shí)間來換取空間資源,減少了空間資源 的占用,只需要兩個(gè)LFSR 結(jié)構(gòu),解決了生成大量LFSR 結(jié)構(gòu)的工作量問題,方便地實(shí)現(xiàn) 了SPGD 控制算法要求的多路、獨(dú)立偽隨機(jī)序列的生成,并提出了解決了Gold 序列非平 衡性問題的方法。
-
FPGA
+關(guān)注
關(guān)注
1626文章
21671瀏覽量
601895 -
集成電路
+關(guān)注
關(guān)注
5381文章
11389瀏覽量
360886 -
譯碼器
+關(guān)注
關(guān)注
4文章
310瀏覽量
50280
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
切換變倍光學(xué)系統(tǒng)設(shè)計(jì)
OCAD光學(xué)系統(tǒng)自動(dòng)設(shè)計(jì)程序
自適應(yīng)光學(xué)系統(tǒng)的實(shí)時(shí)模式復(fù)原算法
光學(xué)系統(tǒng)設(shè)計(jì)有哪些要求
自適應(yīng)光學(xué)系統(tǒng)畸變技術(shù)可實(shí)現(xiàn)醫(yī)療高清成像
用FPGA硬件實(shí)現(xiàn)多路偽隨機(jī)序列應(yīng)用適應(yīng)光學(xué)SPGD控制算法設(shè)計(jì)

變形鏡是自適應(yīng)光學(xué)系統(tǒng)中常見的一種波前校正器
高斯光學(xué),理想的光學(xué)系統(tǒng)
自適應(yīng)光學(xué)系統(tǒng)的概念和工作原理
光學(xué)系統(tǒng)設(shè)計(jì)流程
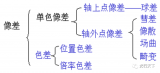
光學(xué)系統(tǒng)設(shè)計(jì)的過程及要求
光學(xué)系統(tǒng)的基本特性
光學(xué)系統(tǒng)設(shè)計(jì)的不可忽略的參數(shù)介紹
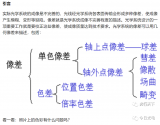




 基于SPGD控制算法自適應(yīng)光學(xué)系統(tǒng)的偽隨機(jī)序列的設(shè)計(jì)與要求
基于SPGD控制算法自適應(yīng)光學(xué)系統(tǒng)的偽隨機(jī)序列的設(shè)計(jì)與要求










評(píng)論