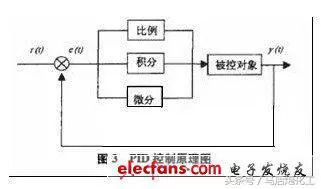
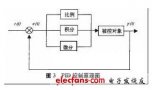
PID控制原理和特點
工程實際中,應用最為廣泛調節器控制規律為比例、積分、微分控制,簡稱PID控制,又稱PID調節。PID控制器問世至今已有近70年歷史,它以其結構簡單、穩定性好、工作可靠、調整方便而成為工業控制主要技術之一。
當被控對象結構和參數不能完全掌握,或不到精確數學模型時,控制理論其它技術難以采用時,系統控制器結構和參數必須依靠經驗和現場調試來確定,這時應用PID控制技術最為方便。即當我們不完全了解一個系統和被控對象﹐或不能有效測量手段來獲系統參數時,最適合用PID控制技術。PID控制,實際中也有PI和PD控制。PID控制器就是系統誤差,利用比例、積分、微分計算出控制量進行控制。
1、比例控制(P):
比例控制是最常用的控制手段之一,比方說我們控制一個加熱器的恒溫100度,當開始加熱時,離目標溫度相差比較遠,這時我們通常會加大加熱,使溫度快速上升,當溫度超過100度時,我們則關閉輸出,通常我們會使用這樣一個函數
e(t) = SP – y(t)-
u(t) = e(t)*P
SP——設定值
e(t)——誤差值
y(t)——反饋值
u(t)——輸出值
P——比例系數
滯后性不是很大的控制對象使用比例控制方式就可以滿足控制要求,但很多被控對象中因為有滯后性。
也就是如果設定溫度是200度,當采用比例方式控制時,如果P選擇比較大,則會出現當溫度達到200度輸出為0后,溫度仍然會止不住的向上爬升,比方說升至230度,當溫度超過200度太多后又開始回落,盡管這時輸出開始出力加熱,但溫度仍然會向下跌落一定的溫度才會止跌回升,比方說降至170度,最后整個系統會穩定在一定的范圍內進行振蕩。
如果這個振蕩的幅度是允許的比方說家用電器的控制,那則可以選用比例控制
2、比例積分控制(PI):
積分的存在是針對比例控制要不就是有差值要不就是振蕩的這種特點提出的改進,它常與比例一塊進行控制,也就是PI控制。
其公式有很多種,但大多差別不大,標準公式如下:
u(t) = Kp*e(t) + Ki∑e(t) +u0
u(t)——輸出
Kp——比例放大系數
Ki——積分放大系數
e(t)——誤差
u0——控制量基準值(基礎偏差)
大家可以看到積分項是一個歷史誤差的累積值,如果光用比例控制時,我們知道要不就是達不到設定值要不就是振蕩,在使用了積分項后就可以解決達不到設定值的靜態誤差問題,比方說一個控制中使用了PI控制后,如果存在靜態誤差,輸出始終達不到設定值,這時積分項的誤差累積值會越來越大,這個累積值乘上Ki后會在輸出的比重中越占越多,使輸出u(t)越來越大,最終達到消除靜態誤差的目的
PI兩個結合使用的情況下,我們的調整方式如下:
1、先將I值設為0,將P值放至比較大,當出現穩定振蕩時,我們再減小P值直到P值不振蕩或者振蕩很小為止(術語叫臨界振蕩狀態),在有些情況下,我們還可以在些P值的基礎上再加大一點。
2、加大I值,直到輸出達到設定值為止。
3、等系統冷卻后,再重上電,看看系統的超調是否過大,加熱速度是否太慢。
通過上面的這個調試過程,我們可以看到P值主要可以用來調整系統的響應速度,但太大會增大超調量和穩定時間;而I值主要用來減小靜態誤差。
pid 算法
控制點目前包含三種比較簡單的PID控制算法,分別是:增量式算法,位置式算法,微分先行。這三種是最簡單的基本算法,各有其特點,一般能滿足控制的大部份要求:
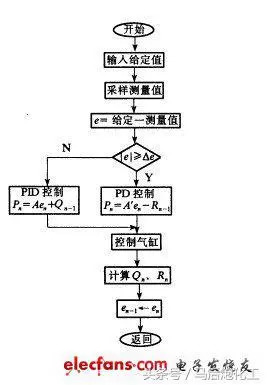
1、PID增量式算法
離散化公式(注:各符號含義如下):
u(t)----- 控制器的輸出值。
e(t)----- 控制器輸入與設定值之間的誤差。
Kp------- 比例系數。
Ti------- 積分時間常數。
Td------- 微分時間常數。
T-------- 調節周期。
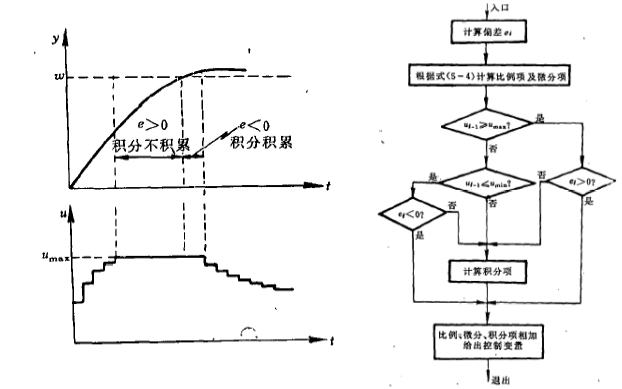
2、積分分離法
離散化公式:
Δu(t) = q0e(t) + q1e(t-1) + q2e(t-2)
當|e(t)|≤β時
q0 = Kp(1+T/Ti+Td/T)
q1 = -Kp(1+2Td/T)
q2 = Kp Td /T
當|e(t)|>β時
q0 = Kp(1+Td/T)
q1 = -Kp(1+2Td/T)
q2 = Kp Td /T
u(t) = u(t-1) + Δu(t)
注:各符號含義如下
u(t)----- 控制器的輸出值。
e(t)----- 控制器輸入與設定值之間的誤差。
Kp------- 比例系數。
Ti------- 積分時間常數。
Td------- 微分時間常數。(有的地方用"Kd"表示)
T-------- 調節周期。
β------- 積分分離閾值
3、微分先行PID算法
離散化公式:
u(t)----- 控制器的輸出值。
e(t)----- 控制器輸入與設定值之間的誤差。
Kp------- 比例系數。
Ti------- 積分時間常數。
Td------- 微分時間常數。(有的地方用"Kd"表示)
T-------- 調節周期。
β------- 積分分離閾值
PID控制:
因為PI系統中的I的存在會使整個控制系統的響應速度受到影響,為了解決這個問題,我們在控制中增加了D微分項,微分項主要用來解決系統的響應速度問題,其完整的公式如下:
u(t) = Kp*e(t) + Ki∑e(t) + Kd[e(t) – e(t-1)]+u0
在PID的調試過程中,我們應注意以下步驟:
1、 關閉I和D,也就是設為0.加大P,使其產生振蕩;
2、 減小P,找到臨界振蕩點;
3、 加大I,使其達到目標值;
4、重新上電看超調、振蕩和穩定時間是否吻合要求;
5、 針對超調和振蕩的情況適當的增加一些微分項;
6、 注意所有調試均應在最大爭載的情況下調試,這樣才能保證調試完的結果可以在全工作范圍內均有效;
PID控制器參數整定
PID控制器參數整定是控制系統設計核心內容。它是被控過程特性確定PID控制器比例系數、積分時間和微分時間大小。
PID控制器參數整定方法很多,概括起來有兩大類:一是理論計算整定法。它主依據系統數學模型,理論計算確定控制器參數。這種方法所到計算數據未必可以直接用,還必須工程實際進行調整和修改。二是工程整定方法,它主要依賴工程經驗,直接控制系統試驗中進行,且方法簡單、易于掌握,工程實際中被廣泛采用。
PID控制器參數工程整定方法,主要有臨界比例法、反應曲線法和衰減法。三種方法各有其特點,其共同點都是試驗,然后工程經驗公式對控制器參數進行整定。但采用哪一種方法所到控制器參數,都需要實際運行中進行最后調整與完善。現一般采用是臨界比例法。利用該方法進行
PID控制器參數整定步驟如下:
(1)首先預選擇一個足夠短采樣周期讓系統工作;
(2)僅加入比例控制環節,直到系統對輸入階躍響應出現臨界振蕩,記下這時比例放大系數和臨界振蕩周期;
(3)一定控制度下公式計算到PID控制器參數。
-
PID
+關注
關注
35文章
1471瀏覽量
85286 -
控制技術
+關注
關注
3文章
342瀏覽量
33144
原文標題:超級實用的PID算法和PID控制原理
文章出處:【微信號:gongkongBBS,微信公眾號:工控網智造工程師】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
模糊PID控制算法如何控制勻速升溫
數字PID控制算法教程之如何對標準PID算法進行改進
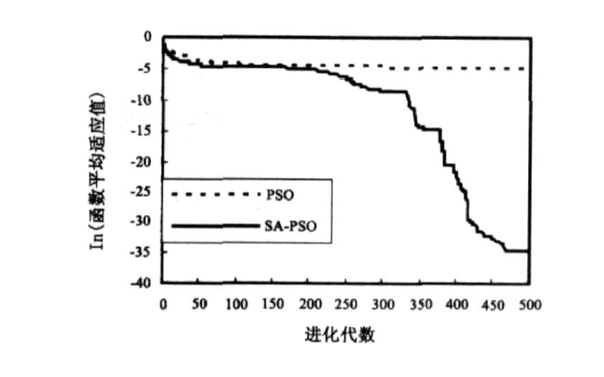
如何使用免疫粒子群優化算法實現增量式的PID控制




 淺析PID算法的控制原理和特點
淺析PID算法的控制原理和特點











評論