作者:葉揚波 著名數學家,美國愛荷華大學教授。作為數論學家,他在中國大陸出版有《跡公式與模形式》等專著。以下是他談Atiyah關于黎曼猜想的證明的文章,觀點專業而且獨到,轉載此文,希望大家能根據此文看到Atiyah證明黎曼猜想的基本思想與價值。
這幾天大家都非常關心Atiyah證明黎曼猜想的事情。作為一名數論工作者,我自然也非常關心,而且反復閱讀了Atiyah的兩篇論文。現在所有的人都在說他的證明不對,我想要進一步弄清楚(1)他是用什么思路什么方法來研究黎曼猜想的,(2)他的所謂證明是否嚴格,(3)即使他的證明是錯的,他的思路方法是否有可取之處。現在談談我的看法,以補充大家的熱議。
問題(2)最容易回答,老先生的文章的確有許多漏洞。比如最關鍵的Todd函數T(s)他說在任意凸區域內是多項式,我覺得他應該說T(s)在凸區域內是局部多項式。他又說T(s)把直線Im(s)=1/2映射到自己,可是又說T(s)在這條直線上的極限為137.035999...他說T(s)在這條直線上是單調增,可是他明明剛說過T(s)在凸區域1/4
更加致命的錯誤可能是用T(s)來證明黎曼猜想。老先生用T(s)和黎曼zeta函數
zeta(s)=1/1^s+1/2^s+1/3^s+...
作了一個復合函數,宣稱該復合函數恒等于零,用這個矛盾推出了黎曼猜想成立。可是這個證明過程中沒有用到zeta(s)的任何性質與定義,也就是說你可以把zeta(s)換成任何其他函數也能證明出來類似的定理。這就有點天方夜譚了。
Atiyah的證明是建立在實數域R上的von Neumann馮·卡門代數A和有理數域Q上的Hirzebruch代數A(Q)上的。這兩個代數超級巨大,比如A是2x2復矩陣代數與自身的無窮張量積的弱閉包。2x2復矩陣有兩個映射到復數域C,為矩陣映到其兩個特征值。老爺子把這兩個映射擴充到A的中心C(A)上,用這兩個映射一來一回定義T(s)。可是矩陣代數的中心不是都由相同對角元素的對角矩陣組成的嗎?這兩個特征值是一樣的對不對?就算兩個特征值不一樣,你憑什么說哪個是第一個哪個是第二個?尤其是還要來一個無窮張量積,全裹和到一塊兒去了,這樣定義出來的T(s)令人費解。
回到問題(1),大家已經看出來了,Atiyah的理論是建立在巨大無比的兩個代數結構上的。這兩個巨大的代數一個在R上,一個在Q上,它們之間的關系包含了所有的數論信息。而以這兩個代數中的元素作為線性算子,它們的特征值為所謂的證明提供了核心的基礎框架。不管證明對不對,上面這幾句話概括了Atiyah的思路與方法。
那么問題(3)來了,到底Atiyah的思路與方法有沒有可取之處?
近年來數論界對黎曼猜想的研究,公認的一個進展是發現黎曼zeta函數的非平凡零點與重原子能級有同樣的統計分布。重原子能級是量子力學中Hamiltonian算子的特征值。這個發現一度被認為是自黎曼猜想之后人類對黎曼zeta函數的第二個重大發現。但是幾年之后一位學者在德國的一家圖書館翻閱黎曼數學手稿,赫然發現黎曼在計算黎曼zeta函數零點的手稿的紙背,寫有大量關于原子能級的計算。這一下真相大白,原來黎曼早就意識到了非平凡零點與重原子能級之間的可能聯系。
從此數論學家們的目標就是要找到這樣一個算子,使得它的特征值是黎曼zeta函數的非平凡零點。然后通過研究這個算子,就像對稱算子特征值均為實數一樣,證明所有非平凡零點的實部均為1/2,從而證明黎曼猜想。而這個思路在有限域上的函數域上已經被證明了。
從這個意義下來說,Atiyah的思路是對的。算子有了,特征值也出現了。是不是他用的von Neumann算子代數和Hirzebruch算子代數真的包含了大家夢寐以求可以用來證明黎曼猜想的那個算子,或者可以在其之上構建出一個,我想這未來的幾年一定會研究輩出。大家翹首以待吧,或者最好親身加入這個研究的行列。這條路如果最終能夠走通,Atiyah的文章就是有歷史意義的了。
-
函數
+關注
關注
3文章
4307瀏覽量
62433 -
ZETA
+關注
關注
0文章
119瀏覽量
10280
原文標題:也談談Atiyah關于黎曼猜想的證明
文章出處:【微信號:AItists,微信公眾號:人工智能學家】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
鴻蒙開發:Universal Keystore Kit密鑰管理服務 密鑰證明介紹及算法規格
循環神經網絡的基本概念
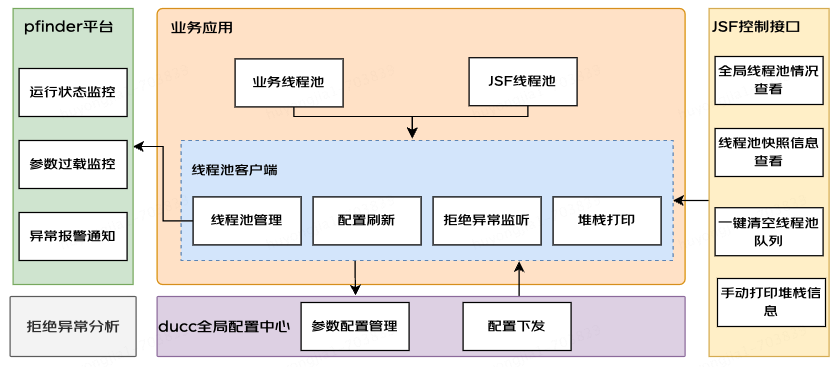
動態線程池思想學習及實踐
信號分析的基本思想是什么
一文了解通信中Polor碼信道聯合極化編碼的基本思想

到底什么是算力?算力的價值在哪里?
場強是電勢的梯度如何證明
從"精益思想"看機器人的開發與應用:一場科技與效率的完美融合
圖像處理怎么入門?
【宇宙猜想】AR文創入駐今日美術館、北京天文館等眾多展館,在AR互動中感受科技魅力!
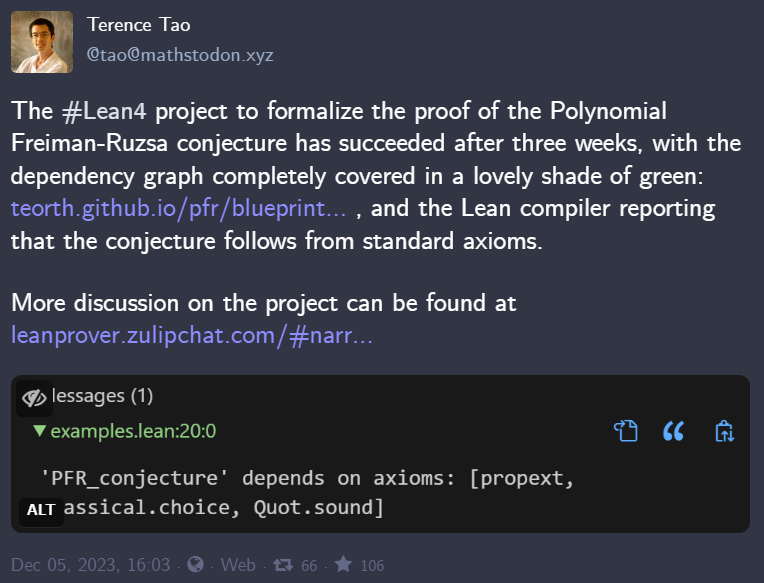
陶哲軒用 AI 形式化的證明究竟是什么?一文看懂 PFR 猜想的前世今生




 Atiyah證明黎曼猜想的基本思想與價值
Atiyah證明黎曼猜想的基本思想與價值










評論