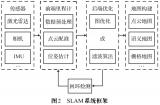
在智能服務機器人逐漸成為行業風口浪尖的今天,移動機器人的身影越來越多地出現在人們身邊。相信隨著傳感技術、智能技術和計算技術等的不斷提高,智能移動機器人一定能夠在生產和生活中融入人類生活中。上一期小編大致介紹了基于概率模型的SLAM方法的基本原理,本期,小編給大家詳細介紹下概率模型SLAM方法中一個比較重要的家族:卡爾曼濾波。
什么是卡爾曼濾波
卡爾曼濾波(Kalman filtering),又稱線性二次型估計(Linear quadratic estimation),是Swerling(1958)和Kalman(1960)作為線性高斯系統中的預測和濾波技術而提出的。
最早由Stanley Schmidt首次實現,后被Kalman發掘并應用于NASA的阿波羅計劃。提到阿波羅計劃,大家可能會有種小編是在幫卡爾曼濾波蹭“人類登月”熱度的感覺,其實不然,在工程領域里,卡爾曼濾波一樣也很“高大上”。
作為線性高斯系統預測方法中最優、最高效的工具,卡爾曼濾波器及其變種已經被廣泛應用在諸如機器人導航,傳感器數據融合,導彈追蹤,人臉識別等多種領域近半個世紀。
卡爾曼濾波解決的問題是“線性高斯系統的預測和濾波”,那么什么是線性高斯系統呢?高斯分布想必大家應該都有所耳聞,或者換個說法,正態分布,這個高中經常被數學老師拿來讓我們估算人群身高分布的“大殺器”。它的長相是下圖這個樣子的:
正態分布很簡單,只需要兩個參數就可以表示了,即期望μ和方差σ。一個多元正態分布的表達式為:
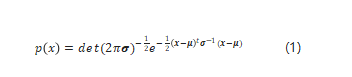
呃,上面的公式看看就好,其實只需要知道正態分布的期望μ就是它的對稱軸,方差σ就是它的“胖瘦”情況,上面的圖中給出了幾個不同μ和σ的正態分布的樣子。一個所謂的“高斯線性系統”需要滿足三個條件:
1)狀態轉移概率p(xt|ut,xt-1)是帶有隨機高斯噪聲的線性函數;
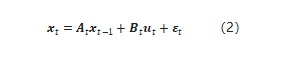
xt是t時刻的狀態向量,它是上一時刻的狀態xt-1和當前時刻的控制量ut的線性組合,εt表示一個隨機的高斯噪聲,它是由狀態轉移引入的不確定性。需要注意的是,式2表達的不是一個確定的解,而是一個分布,它由期望Atxt-1+Btut和方差rt確定。
2)測量概率p(zt|xt)也與帶有高斯噪聲的狀態量呈線性關系;
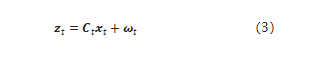
zt是t時刻的測量向量,ωt是測量時的高斯噪聲。同樣,式3也是一個分布,期望是Ctxt,方差是qt。
3) 初始置信度bel(x0)也是正態分布的,它期望是μ0方差是σ0。
如果一個系統能滿足上述三個條件,則它的后驗估計也滿足高斯分布,其期望為μt方差為σt。換句話說,一個最優估計的問題,它的先驗概率分布是高斯分布,同時它的測量概率分布也是高斯分布,那么它的后驗概率也滿足高斯分布,并可求它的期望和方差。
下面拿擎朗智能第三代系列機器人——peanut舉個例子,一輛做勻速運動的peanut,它的初始位置為s0,速度為v,求它在t時刻的位置,大家一定立馬就能給出答案:st=s0+vt。
沒錯,理論上t時刻的位置就應該是這個值。但在實際工程應用中,位置s和速度v并不會是理想值,它會有一定的不確定性,我們假設這個不確定性是滿足高斯分布的。
如果沒有后驗的話,這個不確定性會不斷地疊加,就如上圖(a)所示,隨著peanut的不斷前行,位置s概率分布的方差會越來越大,peanut對自己位置的估計也就越來越不準確。
為了確保位姿估計的準確性,加入了一個觀測值去修正計算得到的速度,例如用里程計去測量每次走過的距離st’,如上圖(b)所示,
藍色表示peanut當前時刻的先驗估計,它由上一時刻的估計值st-1通過運動方程求得;
綠色表示從里程計獲得的觀測值得概率分布,它與先驗估計有一定的偏差;
紫色表示通過卡爾曼濾波后,修正的概率分布。
從濾波的結果來看,后驗估計也是高斯分布,它的分布綜合了先驗和觀測的期望,且縮小了方差。
卡爾曼濾波的一般步驟
通過上面的介紹,相信大家對卡爾曼濾波能干啥應該有個大致的了解了,那么它是如何使用的呢?廢話不多說,先上公式,
卡爾曼濾波的經典五步:
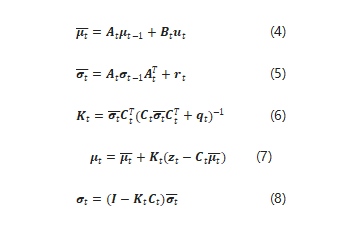
好吧,看到上面的公式大家可能會有點懵,下面小編盡量用比較通俗的語句解釋下,
這五步具體做了什么:
1)計算狀態轉移的期望,μt-1表示上一狀態的期望值,其實就是上一次后驗分布的期望,ut是控制量,這樣就求出了先驗概率分布的期望值;
2)光有期望值還不夠,還需要計算方差才能得到一個完整的正態分布,公式5就是計算先驗概率方差的過程,其中σt-1表示上一次后驗的方差,rt是狀態轉移引入高斯噪聲的方差。
3)得到先驗概率分布后,就需要通過貝葉斯估計求解后驗概率分布。公式6是求解卡爾曼增益K,它通過觀測概率分布的方差qt和先驗概率分布的方差求得。
4)卡爾曼增益K主要用來衡量“預測值”和“觀測值”的比重,即是更相信預測的結果還是更相信觀測的結果;具體表現在公式7,后驗的期望是先驗的期望加上卡爾曼增益乘以估計和觀測期望的偏差。
5)后驗的期望得到后,再通過公式8更新后驗的方差,就得到了后驗估計得概率分布。
通過上述五步就精確地求解了一個“線性高斯系統”的后驗估計,算法里運算量最大的矩陣求逆運算和矩陣乘法運算時間復雜的分別可近似為O(k2.4)和O(k2),k是矩陣維度。相對其他算法,卡爾曼濾波算法是相當高效的。
卡爾曼濾波的變種
卡爾曼濾波雖然高效且精確,但是他有個致命的缺陷,即要求系統是高斯線性的,而實際應用中,絕大多數系統不是高斯線性的。
于是就有了所謂的擴展卡爾曼濾波EKF(Extended Kalman Filter)和無跡卡爾曼濾波UKF(Unscented Kalmen Filter )的變種。
EKF和UKF都是將實際狀態轉移模型局部線性化,只不過前者采用的是泰勒展開進行線性化,而后者采用的是通過加權統計線性回歸過程實現隨機線性化。
通俗的講,EKF是計算非線性函數的切線來進行線性化的,因此EKF需要知道狀態轉移方程的雅可比矩陣(Jacobian Matrix),UKF則是通過提取所謂的δ點,用這些δ點擬合的直線作為局部線性化的參考,δ的取值與分布的協方差有關。
EKF和UKF的算法復雜度近似,一般情況下EKF會稍微快一點,而估計的結果一般情況下UKF要優于EKF。
卡爾曼濾波作為經典的估計算法,被廣泛應用在各個領域之中,在機器人領域里,卡爾曼濾波主要應用在多傳感器融合,SLAM的最優估計等問題中。
以上就是本期關于卡爾曼濾波的內容,下期小編將給大家介紹粒子濾波的相關內容。
-
SLAM
+關注
關注
23文章
419瀏覽量
31789 -
卡爾曼濾波
+關注
關注
3文章
162瀏覽量
24636
原文標題:【Robot 學院】SLAM 技術模型實例:卡爾曼濾波
文章出處:【微信號:robotn,微信公眾號:產業大視野】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
介紹FIR濾波模型的建立,分4個步驟
卡爾曼濾波的優缺點有哪些
計算機視覺技術的AI算法模型
卡爾曼濾波是什么 卡爾曼濾波與目標追蹤技術分析





 詳細介紹概率模型SLAM方法中的卡爾曼濾波
詳細介紹概率模型SLAM方法中的卡爾曼濾波



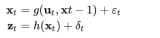
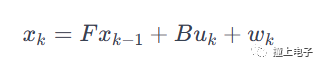











評論