1
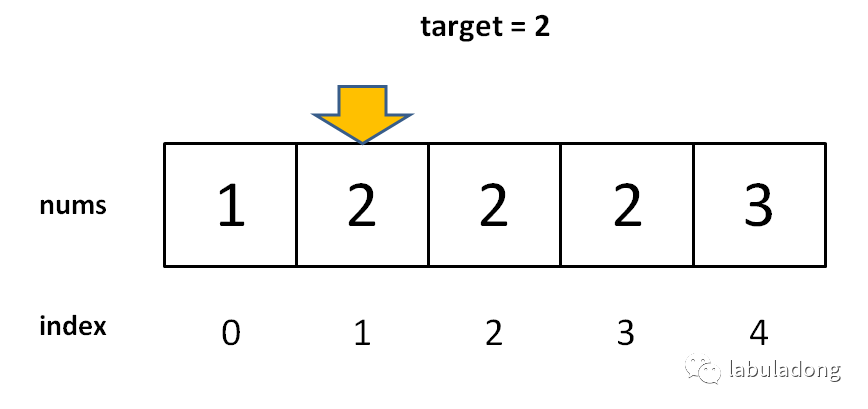
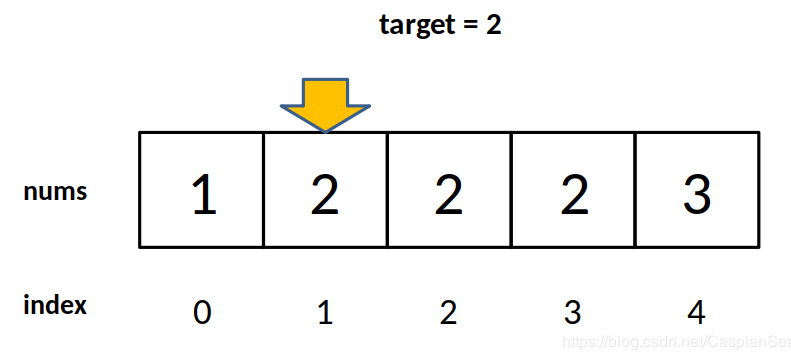
首先問大家一個問題,如果有一堆有序的數據
1,2,3,4,5,6,7,8,9,10,11,...100
如果想要找出55,你要怎么實現呢?
最直觀的是用線性查找,從頭開始一個個的查找,需要55次才能找到目標數值。
如果大家學過C或者C++,應該有二分法查找的概念,先把這堆數分成2堆,把第一堆的最后一個數跟55比較,發現55比它大,所以55應該在第2堆。再重復這個過程,大概需要7次就可以確定55的位置。
二分法查找效率顯而易見,它的時間復雜度T(n)=O(log(2)n),遠遠小于線性查找的T(n)=O(n)。
但二分法要求數據必須是有序排列的,這在實際電路世界里面往往是滿足的。
利用二進制搜索(二分法查找)實現的逐次逼近算法,每次都是選取比較范圍內的中間點來跟參考值進行比較,通過比較結果來繼續縮小比較范圍,一直迭代直至找到最接近比較值的解。
這個過程跟求方程(近似)解也非常類似。二進制搜索實現的逐次逼近常常用于需要校準的場景中,比如SAR ADC、DRAM ZQ 校準、儀器校準算法等。因為我們的校準代碼對應的值是線性增加或者減小的,符合二進制搜索法的條件。
2
下圖是一個SAR ADC的基本架構:
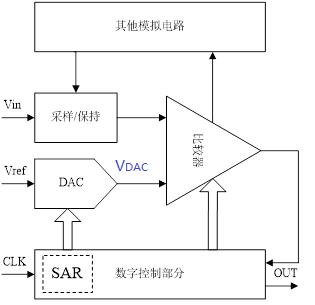
電路的目標就是得到一個最接近Vin的VDAC,可以通過調整
SAR code配置DAC模塊得到。
假設我們的SAR(逐次逼近寄存器)的位數是3位,初始狀態設為SAR[2:0]=3'b100,也就是處于000-111的中間位置。
如果SAR的使能clock 開始toggle,比較過程就開始了:
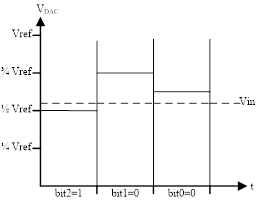
如上圖所示,X軸表示時間,Y軸表示DAC輸出電壓VDAC:
第1次比較: 設置SAR[2:0]=3'b100,VDAC=1/2 Vref < Vin , 所以SAR[2]保持1,SAR[2:0]=3'b100;
第2次比較: 設置SAR[2:0]=3'b110,VDAC=(1/2 Vref + 1/4 Vref)> Vin , 所以SAR[1]最終取0,SAR[2:0]=3'b100;
第3次比較: 設置SAR[2:0]=3'b101,VDAC=(1/2 Vref + 1/8 Vref)> Vin , 所以SAR[0]最終取0,SAR[2:0]=3'b100;
最終我們可以得到與輸入電壓Vin最接近的VDAC,可以看出SAR的位數越多,精度越高,但是比較周期數也會越來越多。
另外其第3次(最后一位)比較好像也沒有必要,因為你比較完也無法得到一個相等值,可以把最后一位固定成1或者0,最大的誤差就是最后一位代表的權重1/8 Vref。
2
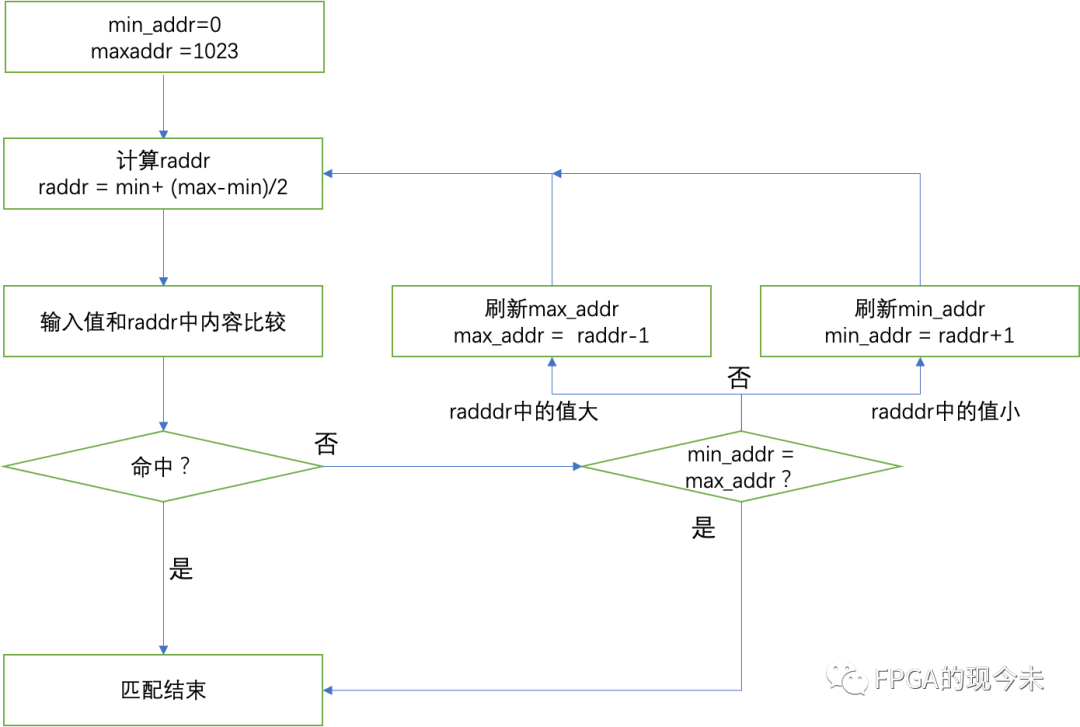
前面是具體的SAR ADC的例子,我們可以進一步把二進制搜索SAR的過程畫成流程圖的形式,方便后續電路或者Verilog代碼的實現:
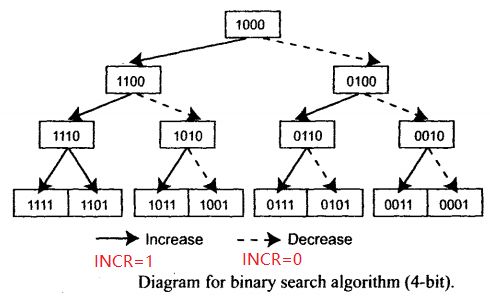
初始化SAR的MSB=1, 其它bit為0 (比如4bit 4'b1000)
每次CLK go high ,走一步
如果INCR=1, 走圖中實線箭頭方向;
如果INCR=0, 走圖中虛線箭頭方向;
最低位LSB最終固定為1
4bit的SAR 一共需要走3步,也就是3個CLK周期后就可以得到最后的結果。
3
最后給出一個6位二進制搜索SAR logic電路的SPEC:
Input
INCR
CLK
OUTPUT
PUCODE [5:0]
你覺得這個電路是用Verilog代碼實現呢?
還是自己搭電路比較好?
-
電路
+關注
關注
172文章
5849瀏覽量
171911 -
二進制
+關注
關注
2文章
794瀏覽量
41600
原文標題:二進制搜索算法(二分法查找)在實際電路中的應用
文章出處:【微信號:icstudy,微信公眾號:跟IC君一起學習集成電路】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Labview實現二分法查找數值區間
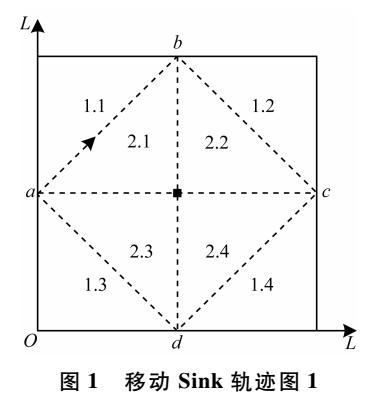
基于二分法與移動Sink的無線傳感器網絡數據收集協議
如何利用verilog驗證二分法查找的設計代碼
如何理解二分查找算法




 二分法查找在實際電路中的應用
二分法查找在實際電路中的應用












評論