多倫多大學的研究人員提出Reversible RNN,一種可以減少RNN訓練時內存需求的新方法,在保留模型性能的同時,將激活內存成本降低了10-15倍。
循環(huán)神經網(wǎng)絡(RNN)在處理序列數(shù)據(jù)方面能有很好的性能,但在訓練時需要大量內存,限制了可訓練的RNN模型的靈活性。
近日,多倫多大學Vector Institute的研究人員提出Reversible RNN,描述了一種可以減少RNN訓練時內存需求的新方法。論文題為Reversible Recurrent Neural Networks,已被NIPS 2018接收。

https://arxiv.org/pdf/1810.10999.pdf
可逆RNN(Reversible RNN)是指網(wǎng)絡中hidden-to-hidden的轉換可以逆向進行的RNN,這就提供了一個減少訓練的內存需求的路徑,因為隱藏狀態(tài)不需要存儲,而是可以在反向傳播期間重新計算。
這篇論文先證明了完全可逆的RNN(perfectly reversible RNNs),即不需要存儲隱藏的激活,在根本是受到限制的,因為它們不能忘記隱藏狀態(tài)的信息。
然后,論文提出一種存儲少量bits的方案,以允許在遺忘時實現(xiàn)完美的逆轉。
這一方法實現(xiàn)了與傳統(tǒng)模型相當?shù)男阅埽瑫r將激活內存成本降低了10-15倍。
研究人員將這一方法擴展到基于注意力的sequence-to-sequence模型,實驗證明能它能保持性能,同時在encoder中將激活內存成本降低了5-10倍,在decoder中降低了10-15倍。
可逆循環(huán)結構
用于構建RevNets的技術可以與傳統(tǒng)的RNN模型結合,產生reversible RNN。在本節(jié)中,我們提出了GRU和LSTM的可逆版本。
Reversible GRU
讓我們首先回顧一下用于計算下一個隱藏狀態(tài)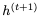 的GRU方程,給定當前隱藏狀態(tài)
的GRU方程,給定當前隱藏狀態(tài)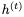 和當前輸入
和當前輸入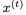 (省略偏差):
(省略偏差):
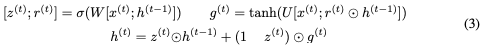
這里,⊙表示elementwise乘法。為了使這個更新可逆,我們將隱藏狀態(tài)h分成兩組,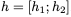 。使用以下規(guī)則更新這些組:
。使用以下規(guī)則更新這些組:
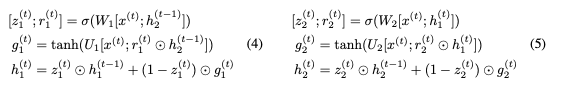
注意,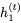 而不是
而不是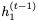 被用于計算
被用于計算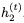 的更新。我們將此模型稱為可逆門控循環(huán)單元(Reversible Gated Recurrent Unit),簡稱RevGRU。
的更新。我們將此模型稱為可逆門控循環(huán)單元(Reversible Gated Recurrent Unit),簡稱RevGRU。
對于i = 1,2,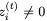 ,因為它是sigmoid函數(shù)的輸出,映射到開放區(qū)間(0,1)。這意味著RevGRU更新在精確算術中是可逆的:給定
,因為它是sigmoid函數(shù)的輸出,映射到開放區(qū)間(0,1)。這意味著RevGRU更新在精確算術中是可逆的:給定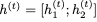 ,我們可以使用
,我們可以使用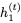
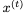
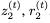 和
和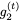 。然后我們可以使用以下公式找到
。然后我們可以使用以下公式找到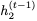 :
:
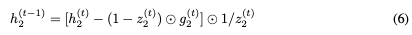
Reversible LSTM
接下來我們構建一個reversible LSTM。LSTM將隱藏狀態(tài)分離為輸出狀態(tài)h和單元狀態(tài)c。更新方程是:

我們不能直接應用可逆技術,因為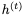
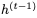 的非零線性變換。但可以使用以下公式實現(xiàn)可逆性:
的非零線性變換。但可以使用以下公式實現(xiàn)可逆性:
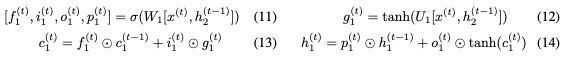
使用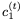 和
和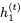 RevLSTM。
RevLSTM。
No Forgetting的限制
我們已經證明,通過確保不丟棄任何信息,可以構建具有有限精度的reversible RNN。
但是,對于語言建模等任務,我們還是無法找到能獲得可接受性能的架構。
我們認為這是由于無遺忘可逆模型(no-forgetting reversible models)的基本限制導致的:如果任何隱藏狀態(tài)都不能被遺忘,那么任何給定時間步長的隱藏狀態(tài)必須包含足夠的信息來重建所有先前的隱藏狀態(tài)。因此,在一個時間步長上,存儲在隱藏狀態(tài)中的任何信息都必須保留在所有未來的時間步長,以確保精確的重構,從而超過了模型的存儲容量。

圖1:在重復任務上展開完全可逆模型的反向計算,得到sequence-to-sequence計算。左:重復任務本身,其中模型重復每個輸入標記。 右:展開逆轉。模型有效地使用最終隱藏狀態(tài)來重建所有輸入tokens,這意味著整個輸入序列必須存儲在最終隱藏狀態(tài)中。
我們通過考慮一個基本的序列學習任務,即重復任務,來說明這個問題。在這個任務中,RNN被輸入一個離散token的序列,并且必須在隨后的時間步長中簡單地重復每個token。
普通的RNN模型只需要少量的隱藏單元就可以輕松解決這個任務,因為它不需要建模長距離依賴關系。但請考慮一個完全可逆的模型如何執(zhí)行重復任務。
展開反向計算,如圖1所示,顯示了sequence-to-sequence的計算,其中編碼器和解碼器權重相關聯(lián)。編碼器接收token并產生最終隱藏狀態(tài)。解碼器使用該最終隱藏狀態(tài)以反向順序產生輸入序列。
我們通過實驗證實,容量有限的NF-RevGRU和NF-RevLSM網(wǎng)絡無法解決重復任務。
有限遺忘實現(xiàn)可逆性
由于No Forgetting不可能,我們需要探索實現(xiàn)可逆性的第二種可能:在正向運算期間存儲隱藏狀態(tài)丟失的信息,然后在反向計算終恢復它。
我們研究了fractional forgetting,即允許遺忘一小部分bits。
算法1描述了可逆乘法的完整過程。

實驗和結果
我們在兩個標準RNN任務上評估了可逆模型的性能:語言建模和機器翻譯。我們希望確定使用我們開發(fā)的技術可以節(jié)省多少內存,這些節(jié)省跟使用理想緩沖區(qū)可能節(jié)省的內存有可比性嗎,以及這些內存節(jié)省是否以降低性能為代價。
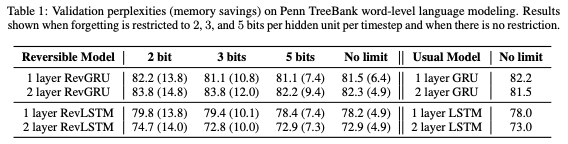
表1:Penn TreeBank詞級語言建模上的驗證困惑度(內存節(jié)省)。當遺忘被限制為每個timestep 每個隱藏單元2、3和5bits,以及沒有限制的情況下的結果。
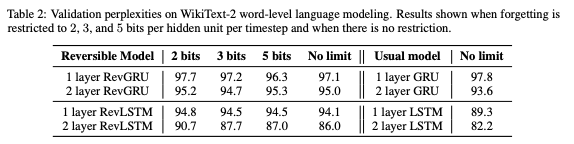
表2:WikiText-2單詞級語言建模的驗證困惑度。當遺忘被限制為每個timestep 每個隱藏單元2、3和5bits,以及沒有限制的情況下的結果。
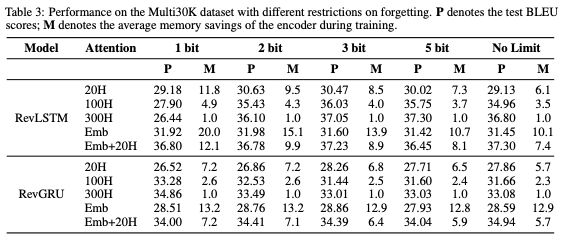
表3:具有不同遺忘限制時Multi30K數(shù)據(jù)集上的性能。P表示測試BLEU scores; M表示訓練期間編碼器的平均內存節(jié)省。
總的來說,雖然Emb attention實現(xiàn)了最佳的內存節(jié)省,但Emb + 20H在性能和內存節(jié)省之間實現(xiàn)了最佳平衡。
具有Emb + 20H attention且遺忘最多2bits的RevGRU實現(xiàn)了34.41的test BLEU score,優(yōu)于標準GRU,同時分別在編碼器和解碼器中將激活內存要求降低了7.1倍和14.8倍。
具有Emb + 20H attention且遺忘最多3bits的RevLSTM的test BLEU score為37.23,優(yōu)于標準LSTM,同時分別在編碼器和解碼器中將激活內存要求降低了8.9倍和11.1倍。
baseline GRU和LSTM模型的測試BLEU分數(shù)分別是16.07和22.35。RevGRU的測試BLEU得分為20.70,優(yōu)于GRU,同時分別在編碼器和解碼器中節(jié)省內存7.15倍和12.92倍。RevLSTM得分為22.34,與LSTM相比,分別在編碼器和解碼器中節(jié)省了8.32倍和6.57倍的內存。兩種可逆模型都被限制為最多遺忘5 bits。
-
神經網(wǎng)絡
+關注
關注
42文章
4765瀏覽量
100568 -
rnn
+關注
關注
0文章
88瀏覽量
6875
原文標題:【NIPS 2018】多倫多大學提出可逆RNN:內存大降,性能不減!
文章出處:【微信號:AI_era,微信公眾號:新智元】歡迎添加關注!文章轉載請注明出處。
發(fā)布評論請先 登錄
相關推薦
一種求解非線性約束優(yōu)化全局最優(yōu)的新方法
一種估計小電流系統(tǒng)線路對地電容的新方法
目前微通道面臨的限制,突破硅技術的一種新方法
一種精確測量儲能成本的新方法:LCUS
一種復制和粘貼URL的新方法
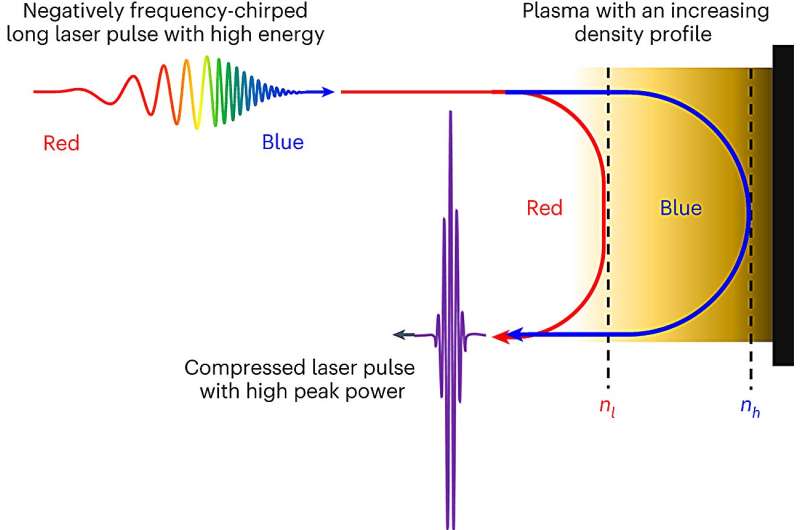
一種產生激光脈沖新方法
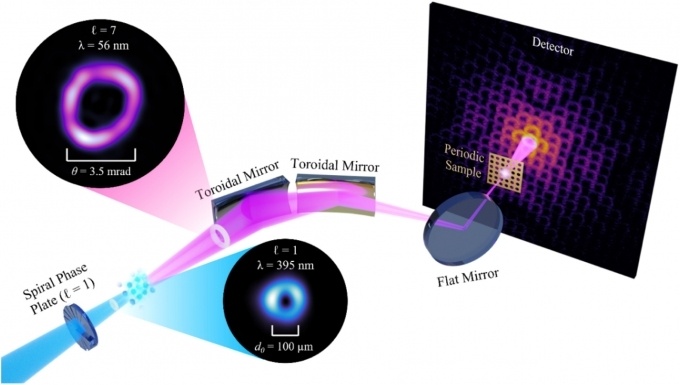
一種無透鏡成像的新方法




 一種可以減少RNN訓練時內存需求的新方法
一種可以減少RNN訓練時內存需求的新方法











評論