昨天跟一個CSDN上的朋友聊天，他說現在如果讓他自己手寫一個棧或者隊列，估計都要寫蠻久的，平時雖然都在用，但是都是別人封裝好的集合。

確實，經典的數據結構，包括排序算法，雖然我們平時不用手寫了，但是這些內功，作為開發人員來說是必須要掌握的。受此啟發，我打算更一下經典數據結構和算法的系列文章。今天先從棧和隊列說起。

這些東西，擠地鐵時，吃飯排隊時，等公交時，可以拿來看看，或者，就把它當作個下午茶吧~

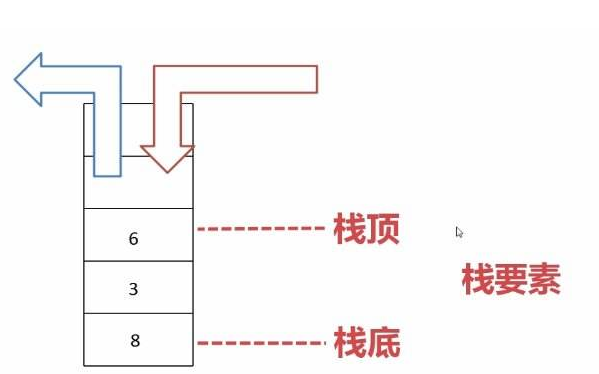
我們知道，在數組中，若知道數據項的下標，便可立即訪問該數據項，或者通過順序搜索數據項，訪問到數組中的各個數據項。但是棧和隊列不同，它們的訪問是受限制的，即在特定時刻只有一個數據項可以被讀取或者被刪除。眾所周知，棧是先進后出，只能訪問棧頂的數據，隊列是先進先出，只能訪問頭部數據。這里不再贅述。

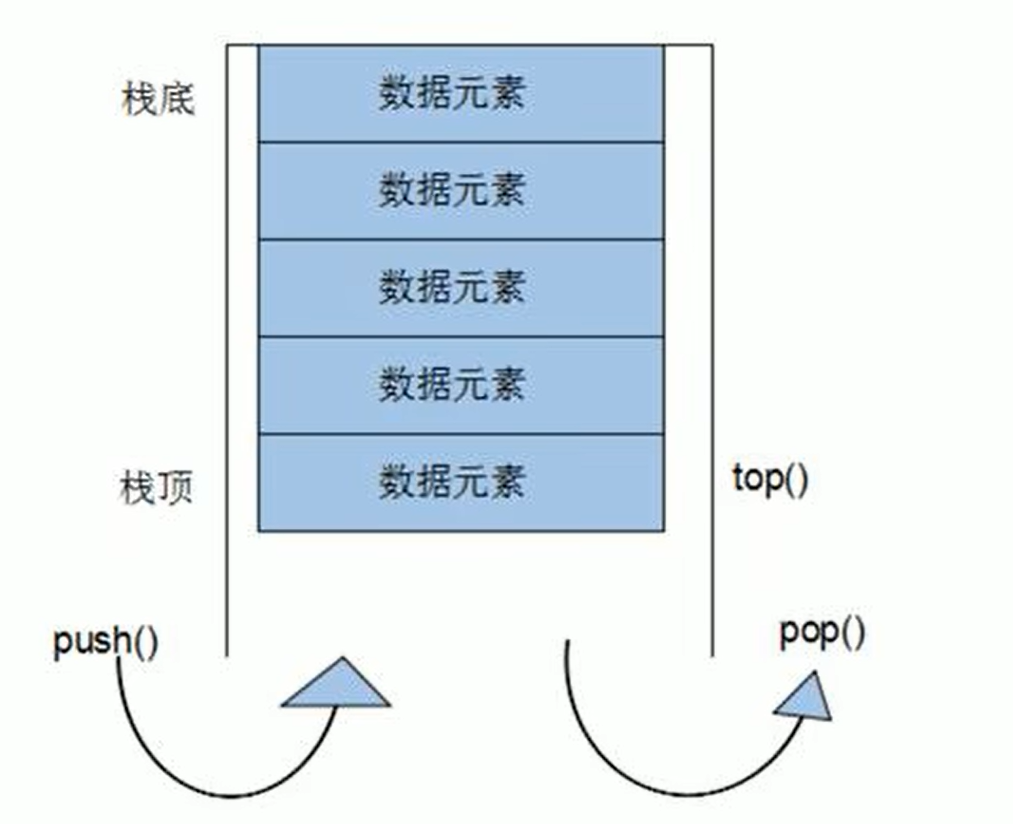
棧的主要機制可以用數組來實現，也可以用鏈表來實現，下面用數組來實現棧的基本操作：

classArrayStack{

privatelong[] a;

privateint size;//棧數組的大小

privateint top;//棧頂

publicArrayStack(int maxSize){

this.size = maxSize;

this.a =newlong[size];

this.top =-1;//表示空棧

}

publicvoid push(long value){//入棧

if(isFull()){

System.out.println("棧已滿！");

return;

}

a[++top]= value;

}

publiclong peek(){//返回棧頂內容，但不刪除

if(isEmpty()){

System.out.println("棧中沒有數據");

return0;

}

return a[top];

}

publiclong pop(){//彈出棧頂內容，刪除

if(isEmpty()){

System.out.println("棧中沒有數據！");

return0;

}

return a[top--];

}

publicint size(){

return top +1;

}

publicboolean isEmpty(){

return(top ==-1);

}

publicboolean isFull(){

return(top == size -1);

}

publicvoid display(){

for(int i = top; i >=0; i--){

System.out.print(a[i]+" ");

}

System.out.println("");

}

}

數據項入棧和出棧的時間復雜度均為O(1)。這也就是說，棧操作所消耗的時間不依賴于棧中數據項的個數，因此操作時間很短。棧不需要比較和移動操作。

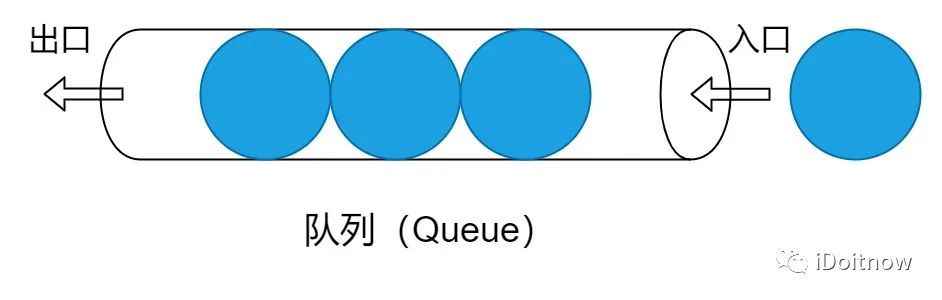
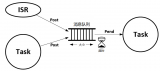
隊列也可以用數組來實現，不過這里有個問題，當數組下標滿了后就不能再添加了，但是數組前面由于已經刪除隊列頭的數據了，導致空。所以隊列我們可以用循環數組來實現，見下面的代碼：

publicclassRoundQueue{

privatelong[] a;

privateint size; //數組大小

privateint nItems;//實際存儲數量

privateint front;//頭

privateint rear; //尾

publicRoundQueue(int maxSize){

this.size = maxSize;

a =newlong[size];

front =0;

rear =-1;

nItems =0;

}

publicvoid insert(long value){

if(isFull()){

System.out.println("隊列已滿");

return;

}

rear =++rear % size;

a[rear]= value;//尾指針滿了就循環到0處,這句相當于下面注釋內容

nItems++;

/* if(rear == size-1){

rear = -1;

}

a[++rear] = value;

*/

}

publiclong remove(){

if(isEmpty()){

System.out.println("隊列為空！");

return0;

}

nItems--;

front = front % size;

return a[front++];

}

publicvoid display(){

if(isEmpty()){

System.out.println("隊列為空！");

return;

}

int item = front;

for(int i =0; i < nItems; i++){

System.out.print(a[item++% size]+" ");

}

System.out.println("");

}

publiclong peek(){

if(isEmpty()){

System.out.println("隊列為空！");

return0;

}

return a[front];

}

publicboolean isFull(){

return(nItems == size);

}

publicboolean isEmpty(){

return(nItems ==0);

}

publicint size(){

return nItems;

}

}

和棧一樣，隊列中插入數據項和刪除數據項的時間復雜度均為O(1)。

還有個優先級隊列，優先級隊列是比棧和隊列更專用的數據結構。優先級隊列與上面普通的隊列相比，主要區別在于隊列中的元素是有序的，關鍵字最小（或者最大）的數據項總在隊頭。數據項插入的時候會按照順序插入到合適的位置以確保隊列的順序。優先級隊列的內部實現可以用數組或者一種特別的樹——堆來實現。

publicclassPriorityQueue{

privatelong[] a;

privateint size;

privateint nItems;//元素個數

publicPriorityQueue(int maxSize){

size = maxSize;

nItems =0;

a =newlong[size];

}

publicvoid insert(long value){

if(isFull()){

System.out.println("隊列已滿！");

return;

}

int j;

if(nItems ==0){//空隊列直接添加

a[nItems++]= value;

}

else{//將數組中的數字依照下標按照從大到小排列

for(j = nItems-1; j >=0; j--){

if(value > a[j]){

a[j+1]= a[j];

}

else{

break;

}

}

a[j+1]= value;

nItems++;

}

}

publiclong remove(){

if(isEmpty()){

System.out.println("隊列為空！");

return0;

}

return a[--nItems];

}

publiclong peekMin(){

return a[nItems-1];

}

publicboolean isFull(){

return(nItems == size);

}

publicboolean isEmpty(){

return(nItems ==0);

}

publicint size(){

return nItems;

}

publicvoid display(){

for(int i = nItems-1; i >=0; i--){

System.out.print(a[i]+" ");

}

System.out.println(" ");

}

}

這里實現的優先級隊列中，插入操作需要 O(N) 的時間，而刪除操作則需要 O(1) 的時間。