哈希表Hashtable是計(jì)算機(jī)中最常見也最基本的數(shù)據(jù)結(jié)構(gòu)之一，但是有的CS基礎(chǔ)不扎實(shí)的學(xué)習(xí)者，其實(shí)還是對這個(gè)結(jié)構(gòu)一知半解，時(shí)時(shí)感到困惑。對于這部分朋友，不妨嘗試一種全新的方式——從創(chuàng)造者的角度，自己把這個(gè)結(jié)構(gòu)重新發(fā)明一遍。這個(gè)想法聽來奇怪，這不是更難了嗎？其實(shí)不然，重在節(jié)奏。只要把思路梳理清楚，把問題一步步分解，你會(huì)看見一條自然清晰的道路。

從發(fā)明的角度，我們只要問兩點(diǎn)：

(1) 我們想解決一個(gè)什么問題？

(2) 這個(gè)問題如何最好地解決？

1

動(dòng)機(jī)：無處不在的查詢

在程序當(dāng)中，經(jīng)常碰到需要“查表”的時(shí)候，就是用某種形式的標(biāo)識（key），去查詢標(biāo)識對應(yīng)的相關(guān)信息（value）：

存一個(gè)用戶名到用戶信息的lookup table，時(shí)時(shí)備查

統(tǒng)計(jì)一段文字的單詞頻率: 那你就得建立一個(gè)從每個(gè)單詞到出現(xiàn)次數(shù)的對應(yīng)關(guān)系，掃描文字的時(shí)候看到哪個(gè)詞就把它的頻次+1

一個(gè)運(yùn)算上成本很高的函數(shù)f(n)，想讓已經(jīng)算過的結(jié)果不再產(chǎn)生重復(fù)勞動(dòng)，那就需要一個(gè)表，存儲(chǔ)所有算過的n，和它們所對應(yīng)的計(jì)算結(jié)果。

這樣的“關(guān)鍵字查詢”需求在程序設(shè)計(jì)的過程中無處不在，所以我們需要一個(gè)高效的機(jī)制，來存儲(chǔ)key和value的對應(yīng)關(guān)系。

2

問題

任務(wù)：設(shè)計(jì)一個(gè)高效率的從key查詢對應(yīng)value的方法。

原料：由于hashtable過于基本，每個(gè)語言都會(huì)有自帶的結(jié)構(gòu)提供這個(gè)功能，不過既然我們在重新設(shè)計(jì)，只能當(dāng)這些語言自帶的的hashtable不存在。你的原料是最基本的，數(shù)組 array。

3

笨辦法

先來個(gè)最最基本的解法，一來幫助理解待解決的問題，二來可以對照出最終hashtable的優(yōu)點(diǎn)。

比如一種笨辦法就是把要存儲(chǔ)的 (key, value) 一對對直接堆放在數(shù)組里

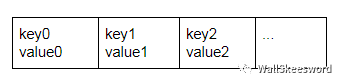
每次查詢一個(gè)key的時(shí)候就從頭到尾掃描數(shù)組，找到key就停，都找遍了就知道沒有這個(gè)key。這個(gè)做法至少滿足了正確性，但是比較慢；因?yàn)榫€性掃描整個(gè)數(shù)組，里面key的總量一多時(shí)間成本就很高。

4

最簡問題：數(shù)組即查詢

回到我們的設(shè)計(jì)問題上。不過你想想，數(shù)組也算是實(shí)現(xiàn)了某種查詢——key都是0..N-1的查詢——輸入下標(biāo) i，數(shù)組 a[i] 告訴你這個(gè)下標(biāo)對應(yīng)的值。

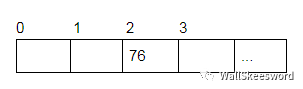
而這也很符合我們的效率需求：查詢和修改都非常快。當(dāng)然，這是因?yàn)閿?shù)組就是連續(xù)內(nèi)存，下標(biāo)就是內(nèi)存取址，所以 0..N-1 相比于別的 key 來說，查詢尤為簡單直接。

那么接下來，我們要問的就是，如何讓任意一種形式的key都可以享有和特殊的 0..N-1 下標(biāo)查詢幾乎一樣的效率呢？一種思路是，只要想辦法高效地把key轉(zhuǎn)化為0..N-1的下標(biāo)就可以了。

5

下標(biāo)轉(zhuǎn)化: key=’a’..’z’

舉例/進(jìn)階題：比如說我們要做一個(gè)簡單的文字加密，我們事先規(guī)定加密關(guān)系 a -> x, b -> o, c -> p, …，把這個(gè)關(guān)系寫進(jìn)一個(gè)lookup table里面，以后加密的時(shí)候，就一個(gè)字母一個(gè)字母地讀原文，查出密文，這個(gè)字母就轉(zhuǎn)化好了。比如單詞 “cab” 就會(huì)變成 “pxo”。

分析：’a’..’z’ 雖然不是整數(shù) 0..N-1 吧，但是也差不多…

一種方案：當(dāng)然是把 ’a’..’z’ 依次序?qū)?yīng)到 0..25 咯

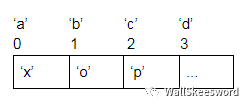
查詢?nèi)魏涡懽帜?ch 的時(shí)候，先計(jì)算出下標(biāo) i = ch - ‘a(chǎn)’，就可以訪問 a[i]，在數(shù)組中查出這個(gè)明文字母該對應(yīng)的密文了。

6

通用轉(zhuǎn)化：hash function

接著上面這個(gè)字母的例子，我們可以籠統(tǒng)地想了，剛才那個(gè)’a’..’z’對應(yīng)到0..N-1的過程，如果能對任何key做就好了。而這個(gè)對應(yīng)機(jī)制，就叫做哈希函數(shù) hash function：如果對于某種 key 類型（比如字符串）我們可以提供一個(gè)哈希函數(shù)hash，把 key 帶進(jìn)去就能輸出一個(gè)整數(shù) hash(key)，那我們可以以它為原料產(chǎn)生數(shù)組下標(biāo)。

通常我們會(huì)讓 hash(key) 大一些，當(dāng)然實(shí)際上數(shù)組空間只有N，所以取個(gè)余數(shù)，以 hash(key) % N 為最終數(shù)組下標(biāo)。比如 hash(key0) % N = 3， 那存成

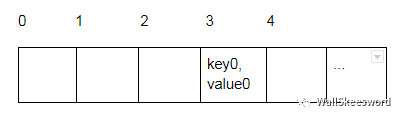
當(dāng)然這只是理想的情況。如果我們觀察 ’a’..’z’ → 0..25 這個(gè)對應(yīng)，就會(huì)發(fā)現(xiàn)它有一個(gè)特殊性，就是“一個(gè)蘿卜一個(gè)坑”：字母和下標(biāo)一一對應(yīng)。但是，在一個(gè)更加一般的情形下，在 hash 函數(shù)和取余數(shù)的雙重操作下，有時(shí)候難免會(huì)出現(xiàn)“很多蘿卜都想去同一個(gè)坑”的狀況。怎么解決呢？人們通常想到兩種辦法：

“把坑挖深”：如果幾個(gè)key都對應(yīng)相同的數(shù)組下標(biāo)，那把這幾個(gè)蘿卜都堆放在這個(gè)坑里面。具體來說每個(gè)數(shù)組下標(biāo)下面掛的不是一對 (key, value)，而是一整個(gè)列表放著若干個(gè) (key, value) ——這個(gè)列表其實(shí)就是類似我們最先提出的那個(gè)“笨辦法”。先用 key 和哈希函數(shù)找到坑，之后在坑內(nèi)查詢就退化成我們的“笨辦法”了。

“先來后到，后到的蘿卜找別的坑占去”：每個(gè)坑還是只容納一個(gè)蘿卜；如果一個(gè)蘿卜發(fā)現(xiàn)自己該去的坑已經(jīng)被占了，可以定義一套規(guī)則，幫助它找下個(gè)坑，一次次直到找到一個(gè)空的坑為止。

7

回顧與想象

以上，我們終于完成了hashtable大體框架的設(shè)計(jì)。想清楚了這些內(nèi)部原理，我們可以開始對它的運(yùn)行開始有一些想象，也作為一種回顧。

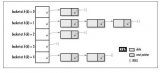
首先，查詢的基本流程如下圖所示，輸入key，通過hash function算出數(shù)組下標(biāo)，然后在這個(gè)數(shù)組下標(biāo)對應(yīng)的坑里面依次尋找這個(gè)具體的key。

在理想的情況下，hash函數(shù)可以成功地把 key 均勻地打散到數(shù)組下標(biāo)中，并且數(shù)組空間也比較充裕，從而 key 的下標(biāo)沖突不多，添加、修改、查詢元素，都可以通過哈希函數(shù)來快速定位，O(1)時(shí)間；偶爾碰見一些下標(biāo)沖突，但是頻率低、多找兩步還是能找到所需元素，那么總體平均下來還是大致認(rèn)為是常數(shù)時(shí)間。

反之，如果hash函數(shù)設(shè)計(jì)得不好，導(dǎo)致下標(biāo)沖突很多，極限情況下可能所有蘿卜都掉進(jìn)一個(gè)坑里，那弄了半天你可能還是退化成了我們最早提出的“笨辦法”。或者數(shù)組空間不足，里面存的 (key, value) 特別多，那可能也會(huì)不得不發(fā)生很多下標(biāo)沖突，非常臃腫，達(dá)不到設(shè)想的效率。