還記得去年戰勝4位專業牌手的德州撲克AI“冷撲大師”嗎？最近，它的締造者、“德州撲克AI之父”Noam Brown和Tuomas Sandholm再發新論文，通過德州撲克基準平臺來探討不完全信息條件下的博弈策略問題，也許“冷撲大師2.0”真的要來了。

最近，Arxiv上的一篇題為《Solving Imperfect-Information Games via Discounted Regret Minimization》引發關注，原因主要在于本文的兩位作者的鼎鼎大名，CMU計算機系博士生Noam Brown，以及該校計算機系教授Tuomas Sandholm。這兩位就是去年的著名的德州撲克AI程序“冷撲大師”（Libratus）的締造者，堪稱德州撲克AI之父。

“冷撲大師”在去年曾與4位人類專業德州撲克牌手大戰20天，最后全面獲勝。兩位作者還去Reddit論壇的機器學習板塊上搞了一次“Ask meanything”的網友問答互動，一時名聲大噪。闡述“冷撲大師”背景技術的論文也被評為NIPS 2017最佳論文。

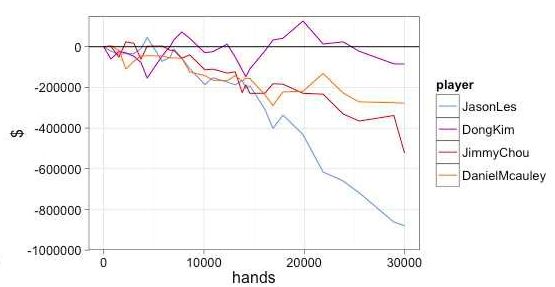
“冷撲大師”在2017年的人機德州撲克大賽面對4位專業人類牌手，全部獲勝

時隔一年多，二位大師再次發布關于不完全信息博弈策略的論文，仍主要以德州撲克為測試基準平臺，難道“冷撲大師”2.0就要來了？人類牌手們，準備好（再次）被碾壓了嗎？

一起看看這篇文章都講了些什么。

論文地址：

https://arxiv.org/abs/1809.04040

摘要

Counterfactual regret minimization（CFR）是目前很流行的一系列迭代算法，實際上也是近似解決大型不完美信息游戲的最快的AI算法。本算法系列中提出了一個“后悔值” （regrets）的概念，即在當前狀態下，選擇行為A，而不是行為B，后悔的值是多少。

在本文中，我們介紹了一些CFR算法的一些新變化，其中包括1）采用多種方法從早期迭代中減低“后悔值”（regret）（在某些情況下對正面和負面后悔值使用不同策略）。（2）以各種方式對迭代進行重新加權，以獲得更佳的輸出策略。（3）使用非標準化的后悔值最小化策略。（4）利用optimistic regret matching。這些方法可以在諸多環境中顯著提高性能。

首先，我們在每個測試的游戲中引入一個優化的CFR +的變體算法，這是之前最先進的算法。CFR+是一個強大的基準，沒有其他算法能夠超越它。我們表明，與CFR +不同，許多基于CFR的重要的新算法與現代不完全信息游戲修剪技術兼容，而且與游戲樹中的樣本兼容。

論文內容提要

不完全信息博弈模擬互相擁有隱藏信息的玩家之間的戰略互搏，比如談判、網絡安全和拍賣都是屬于此類。撲克游戲是這類博弈的常用測試基準。

這種測試的一般目標是找到一種（近似的）均衡，在這種均衡狀態下，沒有玩家可以通過偏離該均衡狀態來提高自己的收益。對于線性程序無法應對的的極大規模的不完全信息博弈，通常使用迭代算法來近似均衡。

CFR方法的主要思想是把游戲中所有狀態都考慮到，生成一顆完整的狀態樹。對樹的每一個節點都初始化一個策略，然后根據這個策略來玩游戲。每次都走狀態樹的一條邊，然后根據游戲的結果來更新相關節點的策略。

當CFR進行了許多次迭代之后，這個狀態樹的每條路徑都被遍歷了很多次，每個節點的策略都被更新趨于均衡了，從而得到一個可以玩游戲的AI。

實驗中使用的游戲——德州撲克和Goofspiel

德州撲克是測試不完全信息博弈算法表現的典型游戲。在本文中使用無限制Heads-up德州撲克規則。兩位玩家（P1和P2）起手籌碼各為20000美元，大/小盲注為50/100美元。每輪加注不得少于100美元。讓對方籌碼降至0者獲勝。

除了德州撲克外，本文采用了另一種紙牌游戲Goofspiel，兩位玩家各擁有5張手牌(A、2、3、4、5)，牌桌中間有5張牌的獎勵牌堆，牌堆中的牌也是A\2\3\4\5。每輪從牌堆中先翻開最上面的牌作為獎勵牌，然后兩名牌手同時出一張手牌比大小，勝者贏得獎勵牌，用過的手牌被棄掉。最后以獎勵牌總分數（A為1分、2為2分，以此類推）多者獲勝。

實驗：CFR的幾種變體和CFR+基準

我們的實驗針對德州撲克進行了32768次迭代，對Goofspiel進行了8192次迭代。由于是近似均衡，而不是精確均衡，所以何時終止迭代計算很大程度上取決于實驗者，一般取100-1000次迭代的結果就是有意義的。

所有實驗都使用CFR的交替更新形式。我們衡量兩個玩家的平均可利用性。我們的實驗表明，在某些游戲中，線性CFR（LCFR）可以在合理的時間范圍內顯著提高CFR +的性能。

然而，LCFR在實際實驗中的表現似乎比CFR+差。線性CFR在Subgame1和3中的表現特別好，與Subgame2和4相比，相對于每個玩家可以下注的最高金額，底池中籌碼價值很小，這時更容易出現嚴重的錯誤行為。在Goofspiel中，線性CFR同樣表現不佳，這表明線性CFR特別適合可能出現嚴重錯誤的游戲。

NormalHedge CFR（NH）是一個在游戲中每個信息集中獨立應用regret最小化的框架。通常，我們使用Regret Matching（RM）作為實現后悔最小化的工具，主要是由于無參數的特點和簡單的實現形式。但是，我們也可以應用任何其他實現regret最小化的工具。

我們使用Normal Hedge（NH）作為CFR中的regret最小化工具進行研究。

NH與RM都具備兩個很理想的特點：都沒有任何參數，并且會向后悔值為負的行為分配“零概率”（這意味著它可以很容易地用于CFR +上）。不過，NH操作在計算上比RM成本更高，因為它涉及取冪和線搜索。

我們發現，NH在具有大錯誤動作的游戲中可能做得更好。在這些實驗中，NH的性能是根據可利用性作為迭代次數的函數來測量的。但是，在我們的實現中，由于NH中涉及取冪和行搜索操作，每次迭代所需的時間要比RM方法長五倍。

因此，使用NH實際上減慢了實踐中的收斂。然而，在指數和線搜索操作的成本無關緊要的某些情況下，比如算法的瓶頸主要在于內存不足，而不是計算速度時，NH方法可能是更好的選擇。

蒙特卡洛CFR（MCCFR）是CFR算法的另一變體，該算法對玩家的某些行為或機會結果進行采樣。).

MCCFR與抽象方法相結合，可以產生最先進的面向德州撲克游戲的AI算法。該模型在沒有特殊結構的博弈中特別有用，可以利用該算法來達成CFR的快速矢量實現。

MCCFR的種類不少，具有不同的采樣方案。最流行的是外部采樣MCCFR，其中根據其概率對對手和機會動作進行采樣，但是遍歷了更新regret值的玩家的所有行動。目前也存在其他性能優異的MCCFR變體，但外部采樣式MCCFR簡單且廣泛使用，可用作我們實驗的基準。

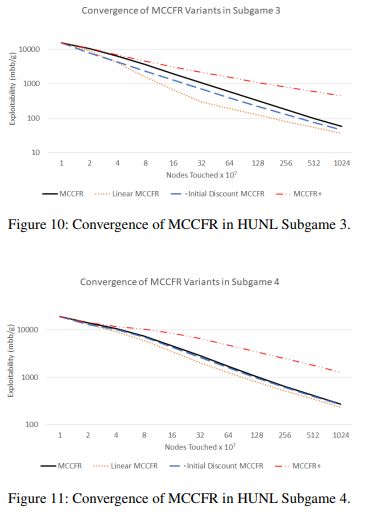
盡管CFR+在非抽樣的情況下體現出比CFR更大的性能改進，但CFR+中的變化，在應用于MCCFR時并不會帶來更優秀的性能。

上圖表明，與vanilla MCCFR相比，模型在德州撲克上具有更優越的表現。在子游戲3（圖中上半部分）中，這種性能提升尤為明顯。

結論

我們在本文中介紹了CFR算法的變體，可以對先前的迭代進行discount，并表現出比之前最先進的CFR +類算法更強大的性能，在涉及重大錯誤的環境中表現的更加明顯。