1 引言
在社會和科學技術日益發展的今天,電力資源的生產和分配成為人們所關注的問題之一,而發電機組的配置對其具有直接的影響。因此,為滿足社會對電力資源的需求,將一日內的 24 小時分為七個時間段,進行合理的生產和分配研究。
電力資源主要由各發電廠提供,而每個發電廠在進行電力資源的生產和分配時,其發電機的所需數量和型號等都不相同,同時投入生產的時間和輸出功率、啟動成本和邊際成本等也不盡相同。而在實際的電力資源的生產和分配中,固定成本、邊際成本和啟動成本在總成本中占主導地位,因此應盡可能減少生產分配中的三種成本,以達到優化的目的。
2 優化模型的建立
2.1 目標函數的建立
為解決本次的電力生產和分配問題,得到最低成本,設總成本 S 由發電機的總固定成本 S1,發電機的總邊際成本 S1 及發電機的總啟動成本 S3 三者組成[2],即 S =S1+S2+S3。而三個分量又由七個時段各型號發電機工作情況所決定,因此有如下關系。
(1)總固定成本。總固定成本由各型號發電機在各時間段內的使用時間 Ti ,使用臺數 Nij 和單位固定成本 Gij 所決定。
(2)總啟動成本:總啟動成本由各型號發電機在各時間段開始時的啟動數量和單位啟動成本所決定,同時考慮到部分發電機在使用過程中不關閉的問題,我們引入 sgn(x) 符號函數,其中 x<0 時 sgn(x) 返回 -1,x=0 時 sgn(x) 返回 0,x>0 時 sgn(x) 返回 1。
(3)總邊際成本:總邊際成本由各型號發電機在各時間段內的使用時間 Ti ,使用臺數 Nij,單位邊際成本 Bij 和實際輸出功率超出最低輸出功率部分所決定。
2.2 優化條件的設置
在實際的電力生產過程中,在任何時刻,正在工作的發電機組必須留出 20% 的發電余量即當前輸出功率不能超出最大輸出功率的 80%,以防因用電量突然上升而導致的損壞。且在某一時段中的發電機總供電量應大于等于此時段中的用電需求。
模型和優化條件的建立,Nij 為時段 i 時型號 j 發電機工作數量;Tij 為時段 i 時間長度;Pij 為在時段 i內型號 j 的平均輸出功率;Qminj 為型號 j 最小輸出功率,Qmaxj 為型號 j 最大輸出功率; Cij、Gij、Bij 分別代表在時段 型號 的單位啟動成本,固定成本和邊際成本。
3 模型在實際生產中的運用
以某地區的實際情況為代表,該地區的 2016 年第一季度中的總用電量為 3.9×109 kW?h,其中工業用電為 3.3×109 kW?h,居民用電量為 6×108 kW?h,當地工業為其支柱產業因此在用電量占比上遠高于居民用電占比,因此主要對該地的工業用電量進行研究。
各型號的發電機組的數量、最小最大輸出功率、固定成本、邊際成本以及啟動成本各有差異。通過對建立的模型和優化條件進行求解,并結合如表 2 的一天七個時間段內用電需求量。
結合電力需求得到四類發電機的需求情況,從使用臺數角度分析,1 號機型和 2 號機型分配臺數較穩定,且各個時間段都有工作;3 號機型在第 1 時間段和第7時間段使用臺數較少,但在其他時間段分配臺數也比較穩定;4 號機型在第 1 時間段不工作,在其他時間段工作臺數波動較大,說明此發電機主要在峰值時期發電。綜合上述的分析,應當根據機組利用的多少,適當增加或減少各機組數量,提高其使用壽命。
從使用功率角度分析,1 號機型、2 號機型發電機輸出功率較穩定,但 3 型號發電機在第 1 時段未使用,在第 7 時段使用功率較低,但其余時間它們均使用功率較高,發電能力的利用率相對而言較高;4型號發電機各時段發電功率不同,且輸出功率變化較大。綜上,結合 4 種不同型號發電機的工作情況,可得出在第 2、4、6 時段電力需求較大。
4 結語
在電力資源的生產和分配的過程中,在保障安全的前提下,最低成本、最高效率地完成生產一直是行業的研究方向。本文在保證 20% 的安全余量的情況下,通過建立生產和分配的模型,并對模型進行約束和優化。將模型運用于實例中時,對問題進行了整體考慮而非局部,得出了全局最優解,快速簡便地獲得了在最低成本下完成電廠發電的方案。能為電廠發電系列問題提供解決思路,具有很高的實用價值。
-
電力
+關注
關注
7文章
2121瀏覽量
50114 -
功率
+關注
關注
13文章
2057瀏覽量
69787 -
發電機
+關注
關注
26文章
1618瀏覽量
67547
原文標題:電力資源生產和分配的優化問題
文章出處:【微信號:appic-cn,微信公眾號:集成電路應用雜志】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
負載箱在確保可靠電力分配中的作用
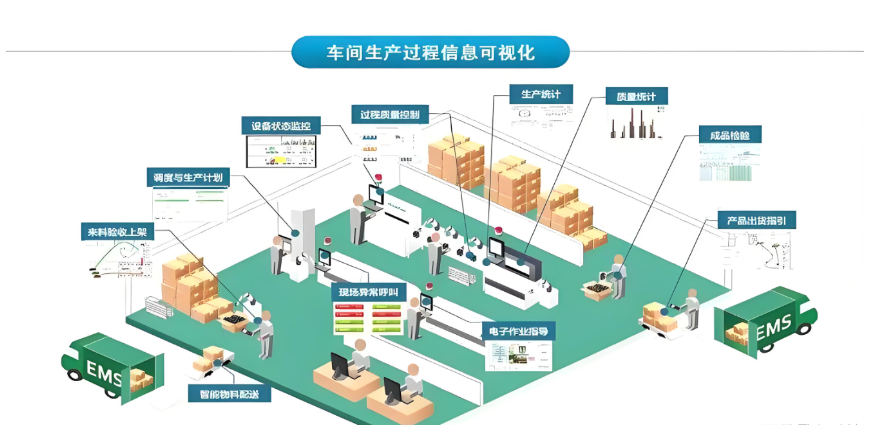
MES系統如何實現生產車間的實時監控、精準調度
物聯網時代下的IP地址分配與管理
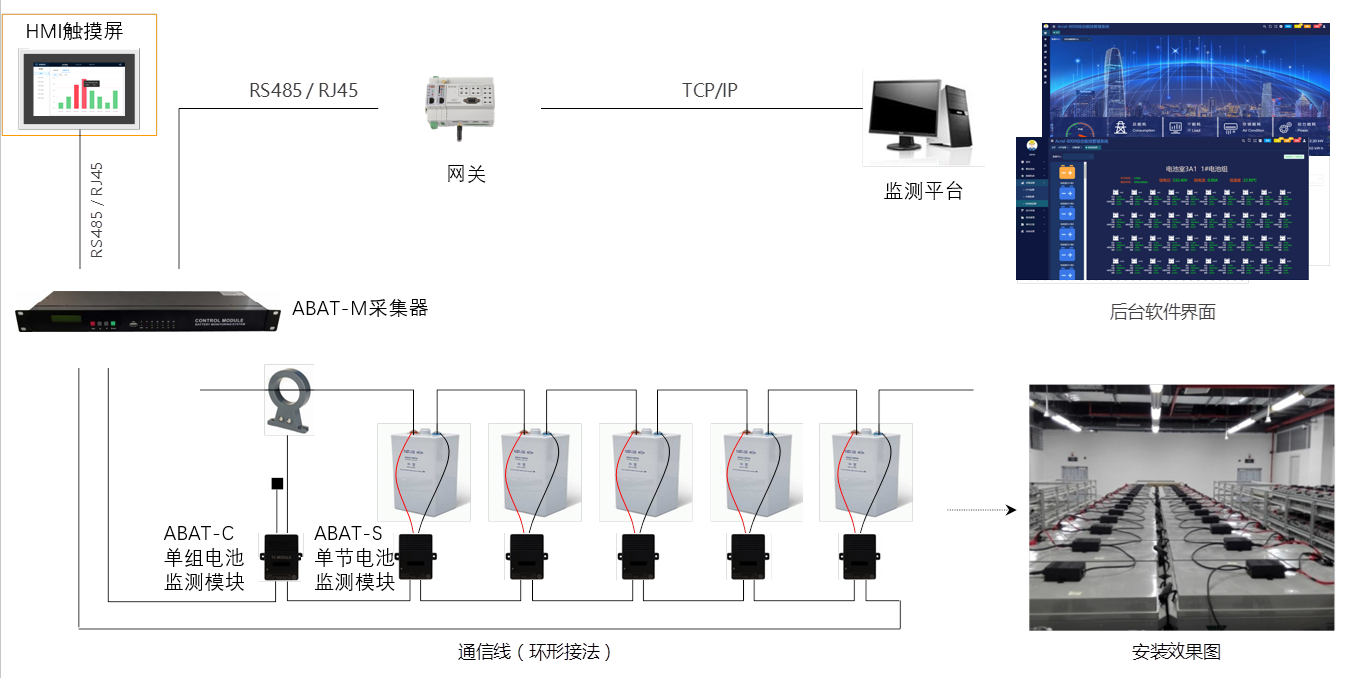
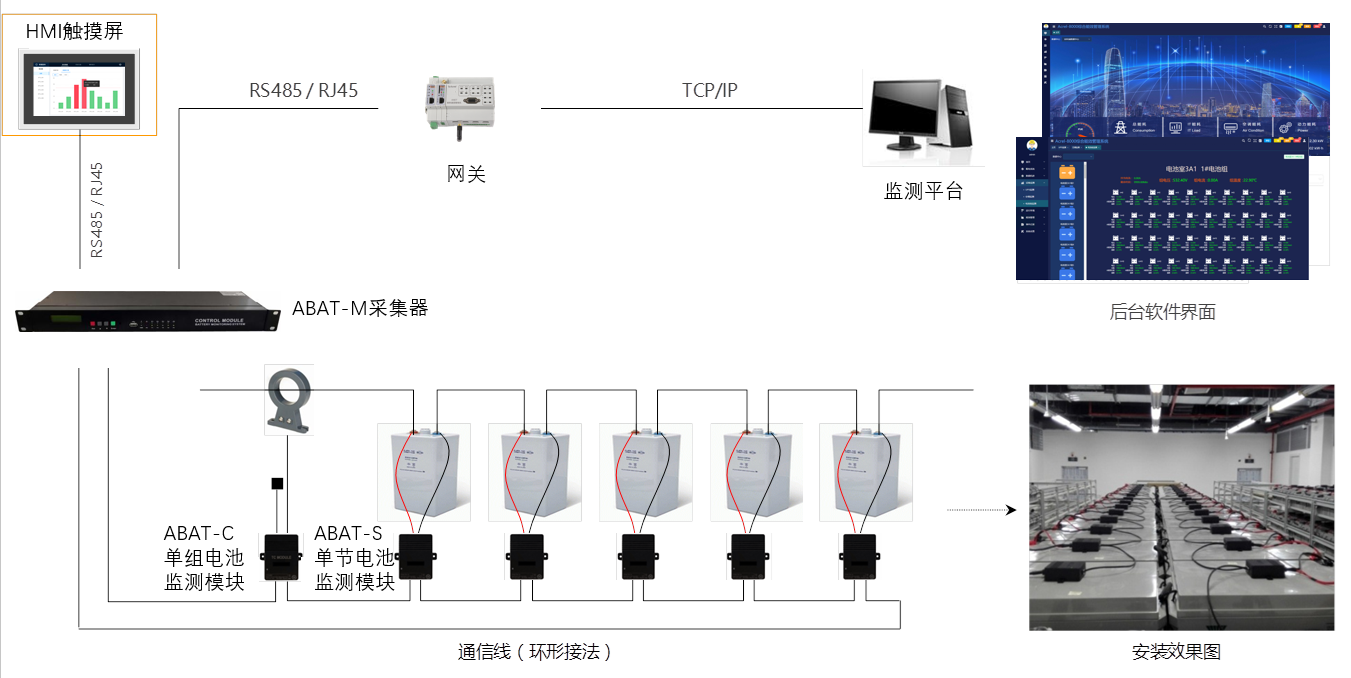
電力分配數據中心蓄電池監測系統
淺談如何克服FPGA I/O引腳分配挑戰
單線分配器與雙線分配器的區別是什么
大型加工企業和各類數據中心電力分配系統
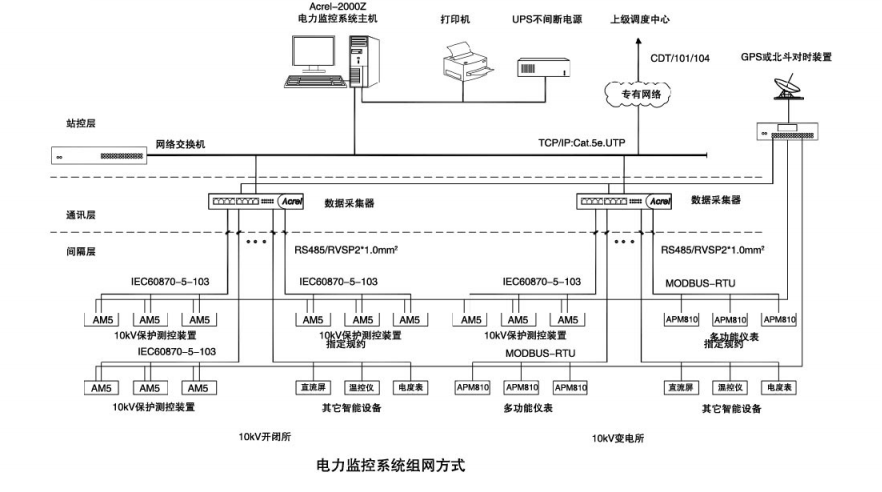
淺談煤礦井下電力監控系統的應用
FPGA管教分配需要考慮因素
淺談智能電力監控系統的研究與運用
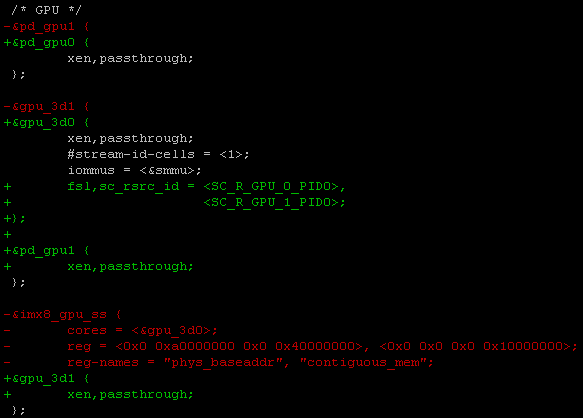
Xen雙系統GPU資源分配過程




 電力資源的生產和分配問題的研究
電力資源的生產和分配問題的研究












評論