大家好,又到了每日學習的時間了,今天咱們來聊一聊數字信號處理中DFT、DTFT和DFS的關系,咱們通過幾幅圖來對比,探討一下哦。
很多同學學習了數字信號處理之后,被里面的幾個名詞搞的暈頭轉向,比如DFT,DTFT,DFS,FFT,FT,FS等,FT和FS屬于信號與系統課程的內容,是對連續時間信號的處理,這里就不過多討論,只解釋一下前四者的關系。
首先說明一下,我不是數字信號處理專家,因此這里只站在學習者的角度以最淺顯易懂的性質來解釋問題,而不涉及到任何公式運算。
學過卷積,我們都知道有時域卷積定理和頻域卷積定理,在這里只需要記住兩點:
1.在一個域的相乘等于另一個域的卷積;
2.與脈沖函數的卷積,在每個脈沖的位置上將產生一個波形的鏡像。
下面,就用這兩條性質來說明DFT,DTFT,DFS,FFT之間的聯系:
先看圖片:
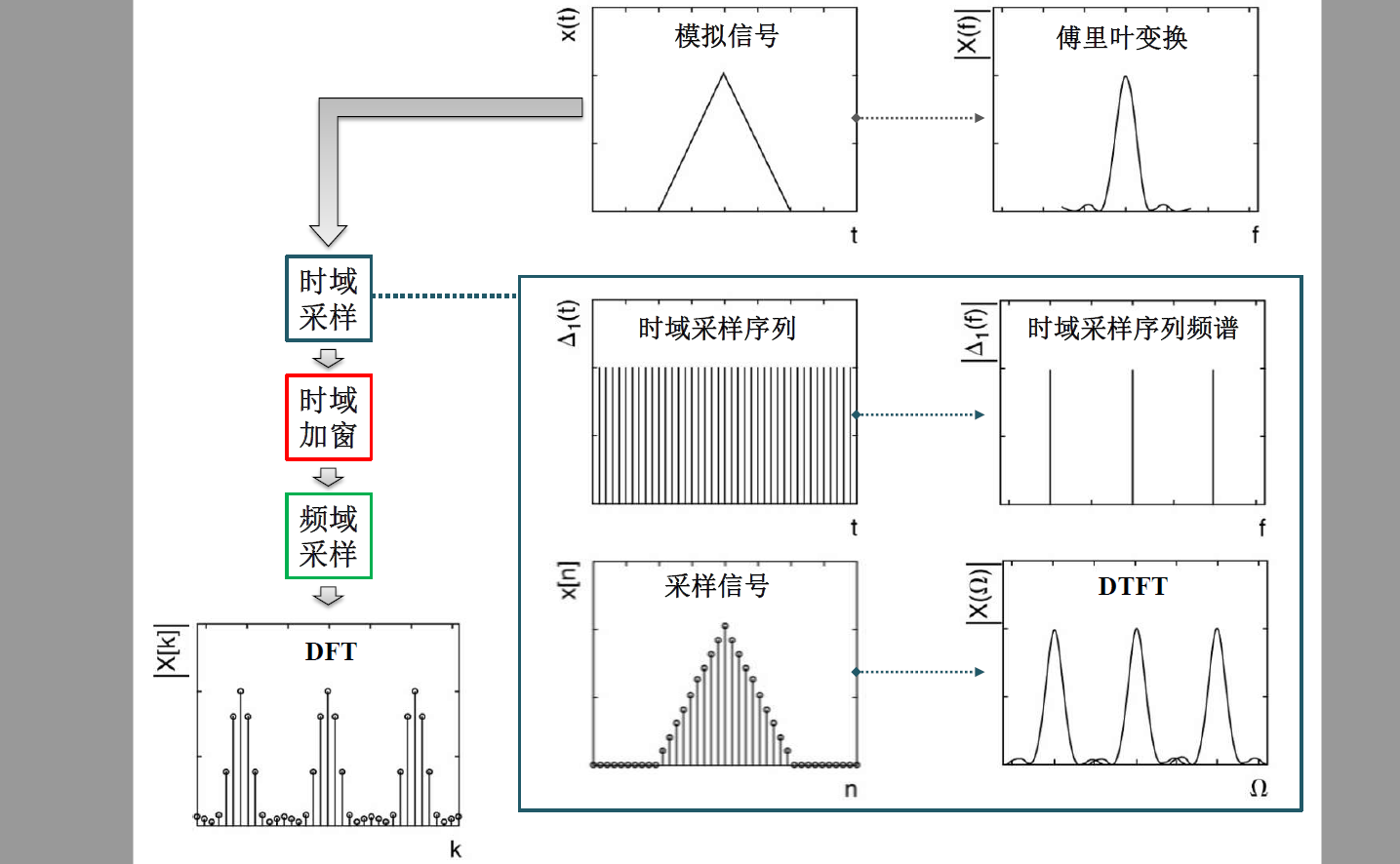
首先來說圖(1)和圖(2),對于一個模擬信號,如圖(1)所示,要分析它的頻率成分,必須變換到頻域,這是通過傅立葉變換即FT(Fourier Transform)得到的,于是有了模擬信號的頻譜,如圖(2)。
注意1:時域和頻域都是連續的!
但是,計算機只能處理數字信號,首先需要將原模擬信號在時域離散化,即在時域對其進行采樣,采樣脈沖序列如圖(3)所示,該采樣序列的頻譜如圖(4),可見它的頻譜也是一系列的脈沖。
所謂時域采樣,就是在時域對信號進行相乘,(1)×(3)后可以得到離散時間信號x[n],如圖(5)所示;由前面的性質1,時域的相乘相當于頻域的卷積。
那么,圖(2)與圖(4)進行卷積,根據前面的性質2知,會在各個脈沖點處出現鏡像,于是得到圖(6),它就是圖(5)所示離散時間信號x[n]的DTFT(Discrete time Fourier Transform),即離散時間傅立葉變換,這里強調的是“離散時間”四個字。
注意2:此時時域是離散的,而頻域依然是連續的。
經過上面兩個步驟,我們得到的信號依然不能被計算機處理,因為頻域既連續,又周期。
我們自然就想到,既然時域可以采樣,為什么頻域不能采樣呢?這樣不就時域與頻域都離散化了嗎?
沒錯,接下來對頻域在進行采樣,頻域采樣信號的頻譜如圖(8)所示,它的時域波形如圖(7)。現在我們進行頻域采樣,即頻域相乘,圖(6)×圖(8)得到圖(10)。
那么根據性質1,這次是頻域相乘,時域卷積了吧,圖(5)和圖(7)卷積得到圖(9),不出所料的,鏡像會呈周期性出現在各個脈沖點處。我們取圖(10)周期序列的主值區間,并記為X(k),它就是序列x[n]的DFT(Discrete Fourier Transform),即離散傅立葉變換。
可見,DFT只是為了計算機處理方便,在頻率域對DTFT進行的采樣并截取主值而已。有人可能疑惑,對圖(10)進行IDFT,回到時域即圖(9),它與原離散信號圖(5)所示的x[n]不同呀,它是x[n]的周期性延拓!
沒錯,因此你去查找一個IDFT的定義式,是不是對n的取值區間進行限制了呢?這一限制的含義就是,取該周期延拓序列的主值區間,即可還原x[n]!FFT呢?FFT的提出完全是為了快速計算DFT而已,它的本質就是DFT!我們常用的信號處理軟件MATLAB或者DSP軟件包中,包含的算法都是FFT而非DFT。DFS,是針對時域周期信號提出的,如果對圖(9)所示周期延拓信號進行DFS,就會得到圖(10),只要截取其主值區間,則與DFT是完全的一一對應的精確關系。
這點對照DFS和DFT的定義式也可以輕易的看出。因此DFS與DFT的本質是一樣的,只不過描述的方法不同而已。不知道經過上面的解釋,您是否明白各種T的關系了呢?如果您不是算法設計者,其實只要懂得如何使用FFT分析頻譜即可,博主近期會更新一篇文章,專門介紹如何利用FFT分析簡單信號的頻譜。其實個人認為,糾結了這么多,就是為了打破現實模擬世界與計算機數字世界的界限呀!今天就聊到這里,各位,加油。
-
數字信號處理
+關注
關注
15文章
557瀏覽量
45795 -
DFT
+關注
關注
2文章
224瀏覽量
22680
原文標題:【FPGA學習】十幅圖教你弄清DFT、DTFT和DFS的關系
文章出處:【微信號:elecfans,微信公眾號:電子發燒友網】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦

來聊一聊Altium中Fill,Polygon Pour,Plane的區別和用法
聊一聊stm32的低功耗調試
數字信號處理教程之DFT和FFT處理的學習課件免費下載




 聊一聊數字信號處理中DFT、DTFT和DFS的關系
聊一聊數字信號處理中DFT、DTFT和DFS的關系










評論