前幾節學習了「鏈表」、「時間與空間復雜度」的概念，本節將結合「循環鏈表」、「雙向鏈表」與 「用空間換時間的設計思想」來設計一個很有意思的緩存淘汰策略：LRU緩存淘汰算法。

三種最常見的鏈表結構

循環鏈表的概念

如上圖所示：單鏈表的尾結點指針指向空地址，表示這就是最后的結點了。而循環鏈表的尾結點指針是指向鏈表的頭結點。

因此循環鏈表是一種特殊的單鏈表。它跟單鏈表唯一的區別就在于尾結點。它像一個環一樣首尾相連，所以叫作「循環鏈表」。

循環鏈表的特點

和單鏈表相比，循環鏈表的優點是從鏈尾到鏈頭比較方便，當要處理的數據具有環型結構特點時，適合采用循環鏈表。

雙向鏈表概念

雙向鏈表也叫雙鏈表，是鏈表的一種，它的鏈接方向是雙向的，它的每個數據結點中都包含有兩個指針，分別指向直接后繼和直接前驅。

所以，從雙向鏈表中的任意一個結點開始，都可以很方便地訪問它的前驅結點和后繼結點。

雙向鏈表的數據結構中，會有兩個比較重要的參數：pre 和 next。

pre 指向前一個數據結構

next 指向下一個數據結構

單鏈表與雙鏈表的對比

雙向鏈表的特點

與單鏈表對比，雙鏈表需要多一個指針用于指向前驅節點，因此如果存儲同樣多的數據，雙向鏈表要比單鏈表占用更多的內存空間

雙鏈表的插入和刪除需要同時維護 next 和 prev 兩個指針。

雙鏈表中的元素訪問需要通過順序訪問，支持雙向遍歷，這就是雙向鏈表操作的靈活性根本

雙向鏈表的基本操作

1.添加元素。

與單向鏈表相對比雙向鏈表可以在 O(1) 時間復雜度搞定，而單向鏈表需要 O(n) 的時間復雜度。

雙向鏈表的添加元素包括頭插法和尾插法。

頭插法和尾插法

頭插法：將鏈表的左邊稱為鏈表頭部，右邊稱為鏈表尾部。頭插法是將右邊固定，每次新增的元素都在左邊頭部增加。

尾插法：將鏈表的左邊稱為鏈表頭部，右邊稱為鏈表尾部。尾插法是將左邊固定，每次新增都在鏈表的右邊最尾部。

2.查詢元素

查詢元素

雙向鏈表的靈活處就是知道鏈表中的一個元素結構就可以向左或者向右開始遍歷查找需要的元素結構。因此對于一個有序鏈表，雙向鏈表的按值查詢的效率比單鏈表高一些。因為，我們可以記錄上次查找的位置 p，每次查詢時，根據要查找的值與 p 的大小關系，決定是往前還是往后查找，所以平均只需要查找一半的數據。

3.刪除元素

在實際的軟件開發中，從鏈表中刪除一個數據無外乎這兩種情況：

刪除結點中“值等于某個給定值”的結點

刪除給定指針指向的結點

刪除元素

對于雙向鏈表來說，雙向鏈表中的結點已經保存了前驅結點的指針，刪除時不需要像單鏈表那樣遍歷。所以，針對第二種情況，單鏈表刪除操作需要 O(n) 的時間復雜度，而雙向鏈表只需要在 O(1) 的時間復雜度。

雙向循環鏈表

雙向循環鏈表

如圖所示，雙向循環鏈表的概念很好理解：「雙向鏈表」 + 「循環鏈表」的組合。

緩存淘汰策略

緩存是一種提高數據讀取性能的技術，在硬件設計、軟件開發中都有著非常廣泛的應用，比如常見的 CPU 緩存、數據庫緩存、瀏覽器緩存等等。

緩存的大小有限，當緩存被用滿時，哪些數據應該被清理出去，哪些數據應該被保留？這就需要緩存淘汰策略來決定。常見的策略有三種：先進先出策略 FIFO（First In，First Out）、最少使用策略 LFU（Least Frequently Used）、最近最少使用策略 LRU（Least Recently Used）。

在各個語言的第三方框架中都大量使用到了 LRU 緩存策略。程序員小吳接觸到的有Java中的 「 Mybatis 」，iOS中的 「YYCache」與「Lottie」等。

LRU緩存淘汰算法

LRU是最近最少使用策略的縮寫，是根據數據的歷史訪問記錄來進行淘汰數據，其核心思想是“如果數據最近被訪問過，那么將來被訪問的幾率也更高”。

LRU概念

鏈表實現LRU

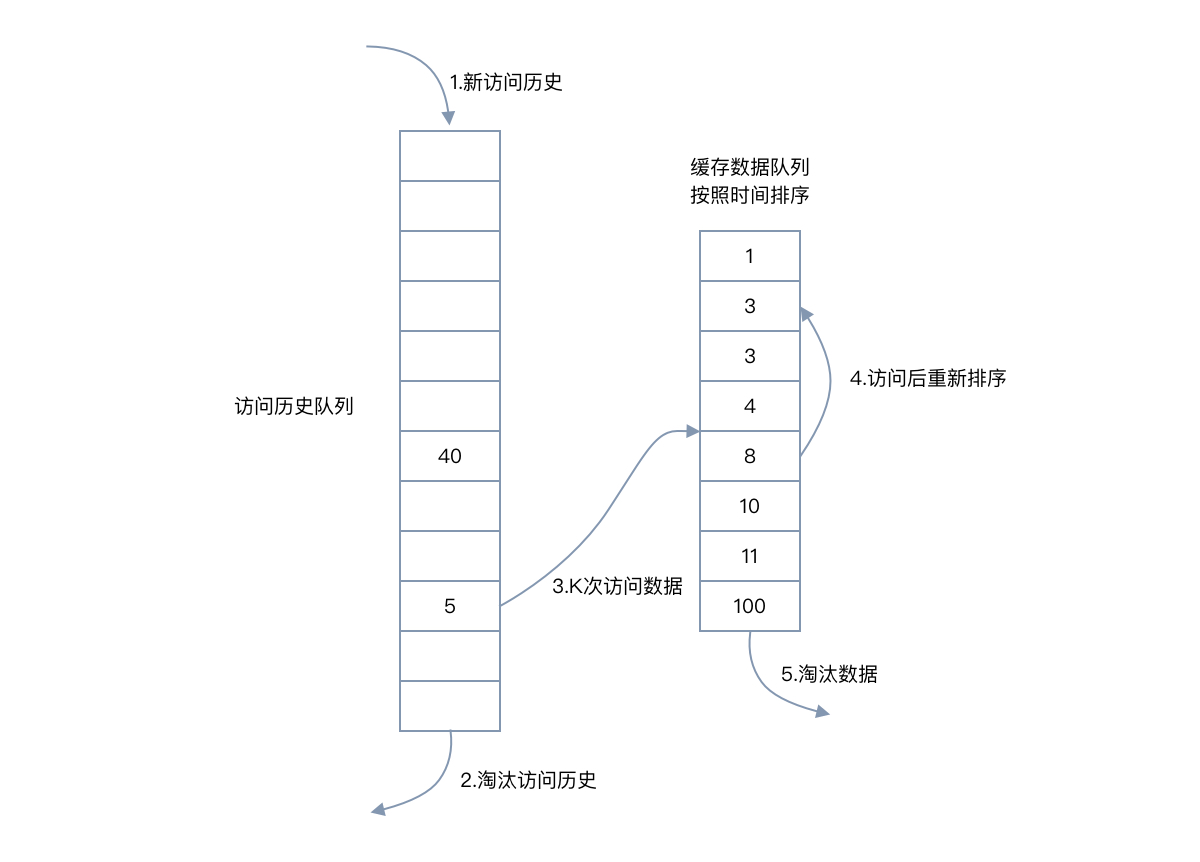
將Cache的所有位置都用雙鏈表連接起來，當一個位置被命中之后，通過調整鏈表的指向，將該位置調整到鏈表頭的位置，新加入的Cache直接加到鏈表頭中。

這樣，在多次進行Cache操作后，最近被命中的，就會被向鏈表頭方向移動，而沒有命中的，而想鏈表后面移動，鏈表尾則表示最近最少使用的Cache。

當需要替換內容時候，鏈表的最后位置就是最少被命中的位置，我們只需要淘汰鏈表最后的部分即可。

鏈表實現LRU動畫演示

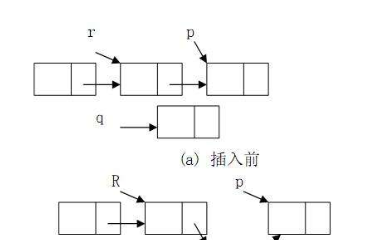
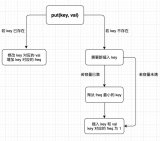
如果此數據之前已經被緩存在鏈表中了，通過遍歷得到這個數據對應的結點，并將其從原來的位置刪除，然后再插入到鏈表的頭部。

如果此數據沒有在緩存鏈表中，可以分為兩種情況：

如果此時緩存未滿，則將此結點直接插入到鏈表的頭部；

如果此時緩存已滿，則鏈表尾結點刪除，將新的數據結點插入鏈表的頭部。

鏈表實現LRU

通過動圖可以發現，如果緩存空間足夠大，那么存儲的數據也就足夠多，通過緩存中命中數據的概率就越大，也就提高了代碼的執行速度。這就是空間換時間的設計思想。

對于程序開發來說，時間復雜度和空間復雜度是可以相互轉化的。說通俗一點，就是：

對于執行的慢的程序，可以通過消耗內存（即構造新的數據結構）來進行優化；

而消耗內存的程序，可以通過消耗時間來降低內存的消耗。