一、KNN回顧

k 近鄰學習是一種常用的監督學習方法，比如：判斷一個人的人品，只需要觀察與他來往最密切的幾個人的人品好壞就可以得出，即“近朱者赤，近墨者黑”。

理論/原理：“物以類聚，人以群分”

相同/近似樣本在樣本空間中是比較接近的，所以可以使用和當前樣本比較近的其他樣本的目標屬性值作為當前樣本的預測值。

k 近鄰法的工作機制很簡單：

給定測試樣本，基于某種距離度量（一般使用歐幾里德距離）找出訓練集中與其最靠近的k個訓練樣本，然后基于這k個“鄰居”的信息來進行預測。

二、KNN三要素

1、K值的選擇

對于K值的選擇，一般根據樣本分布選擇一個較小的值，然后通過交叉驗證來選擇一個比較合適的最終值；

當選擇比較小的K值的時候，表示使用較小領域中的樣本進行預測，訓練誤差會減小，但是會導致模型變得復雜，容易導致過擬合；

當選擇較大的K值的時候，表示使用較大領域中的樣本進行預測，訓練誤差會增大，同時會使模型變得簡單，容易導致欠擬合；

2、距離度量

一般使用歐幾里德距離

關于距離度量，還有其他方式

3、決策規則

KNN在做回歸和分類的主要區別在于最后做預測時的決策方式不同：

（1）分類預測規則：一般采用多數表決法或者加權多數表決法

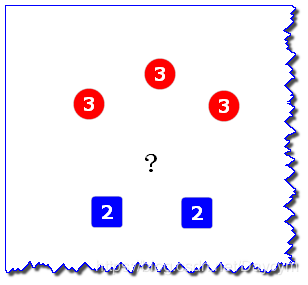
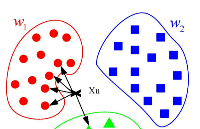
假設圖中 “？”表示待預測樣本，紅色圓表示一類，藍色方塊表示一類，2和3表示到待預測樣本的距離

1. 多數表決法：

每個鄰近樣本的權重是一樣的，也就是說最終預測的結果為出現類別最多的那個類；

如圖，待預測樣本被預測為紅色圓

2. 加權多數表決法：

每個鄰近樣本的權重是不一樣的，一般情況下采用權重和距離成反比的方式來計算，也就是說最終預測結果是出現權重最大的那個類別；

如圖，紅色圓到待預測樣本的距離為3，藍色方塊到待預測樣本的距離為2，權重與距離成反比，所以藍色的權重比較大，待預測樣本被預測為藍色方塊。

（2）回歸預測規則：一般采用平均值法或者加權平均值法

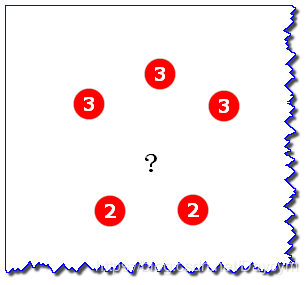
假設上圖中的2和3表示鄰近樣本的目標屬性值（標簽值），此時沒有類別，只有屬性值

1、平均值法

每個鄰近樣本的權重是一樣的，也就是說最終預測的結果為所有鄰近樣本的目標屬性值的均值；

如圖，均值為(3+3+3+2+2)/5=2.6

2、加權平均值法

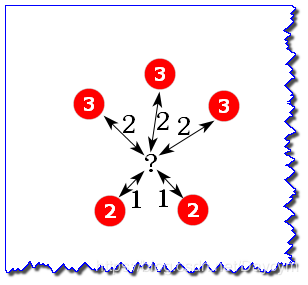
圖中，雙箭頭線上的數表示到待預測樣本的距離

每個鄰近樣本的權重是不一樣的，一般情況下采用權重和距離成反比的方式來計算，也就是說在計算均值的時候進行加權操作；

如圖，權重分別為（各自距離反比占距離反比總和的比例）:

屬性值為3的權重：

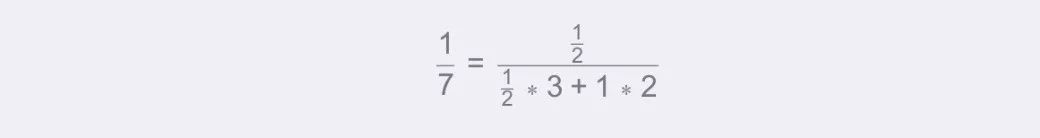
屬性值為2的權重：

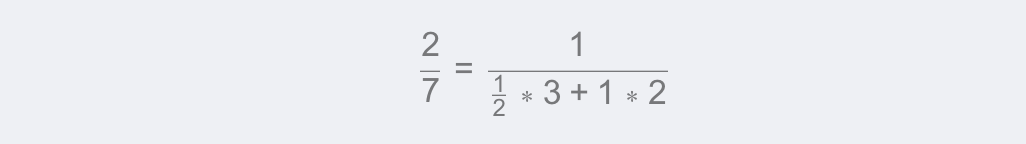
待預測樣本的加權平均值為：

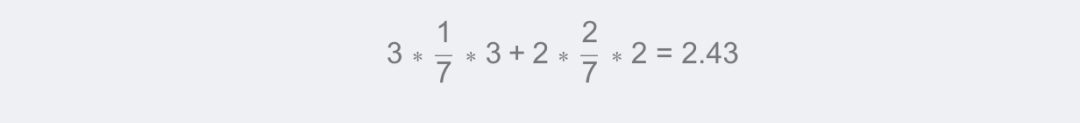
三、手寫 k 近鄰算法

實現kNN分類算法的偽代碼：

對未知類別屬性的數據集中的每個點依次執行一下操作：

（1）計算已知類別數據集中的點與當前點之間的距離

（2）按照距離遞增次序排序

（3）選取與當前點距離最小的k個點

（4）確定前k個點所在類別的出現頻數

（5）返回當前k個點出現頻數最高的類別作為當前點的預測分類

歐氏距離公式：

例如求點(1,0,0,1) (1,0,0,1)(1,0,0,1)和(7,6,9,4) (7,6,9,4)(7,6,9,4)之間的距離：

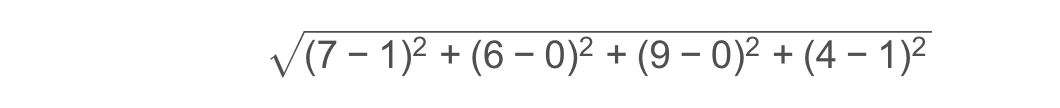
檢測分類器效果：

可以使用已知類別的數據（當然不告訴分類器），檢驗分類器給出的結果是否與已知類別相同，通過大量的測試數據，我們可以計算出分類器的錯誤率。

以上算法的實現是用于分類的，決策規則使用了多數表決法；此算法通過改變決策規則，同樣可以用于回歸。

源代碼可見：https://github.com/Daycym/Machine_Learning/tree/master/03_KNN；01_k近鄰算法.py

四、使用手寫k kk 近鄰算法的案例

1、案例1：約會網站的配對效果

樣本包括3種特征：

每年獲得的飛行常客里程數

玩視頻游戲所耗時間百分比

每周消費的冰淇淋公升數

樣本包括3種標簽：

不喜歡的人

魅力一般的人

極具魅力的人

部分數據格式為：

代碼可見：02_約會網站的配對效果.py

2、案例2：手寫數字識別系統

數據集包括訓練集和測試集

數據是32*32的二進制文本文件

需要將文本數據轉換為Numpy數組

如下是0的一種表示：

100000000000001100000000000000000 200000000000011111100000000000000 300000000000111111111000000000000 400000000011111111111000000000000 500000001111111111111100000000000 600000000111111100011110000000000 700000001111110000001110000000000 800000001111110000001110000000000 90000001111110000000111000000000010000000111111000000011110000000001100000011111100000000011100000000120000001111110000000001110000000013000000111110000000000011100000001400000011111000000000001110000000150000000111110000000000011100000016000000011111000000000001110000001700000001111100000000000111000000180000001111100000000000011100000019000000111110000000000001110000002000000000111100000000000011100000210000000011110000000000011110000022000000001111000000000001111000002300000000111100000000001111100000240000000001111000000000011111000025000000000111110000000011111000002600000000011111000000011111100000270000000001111100000011111100000028000000000111111000111111110000002900000000000111111111111110000000300000000000011111111111110000000031000000000000111111111100000000003200000000000000111110000000000000

預測錯誤的總數為：10

手寫數字識別系統的錯誤率為：0.010571

代碼可見：03_手寫數字識別系統.py

五、KD樹

KNN算法的重點在于找出K個最鄰近的點，主要方法如下：

1、蠻力實現(brute)

計算出待預測樣本到所有訓練樣本的訓練數據，然后選擇最小的K個距離即可得到K個最鄰近點；

當特征數比較多，樣本數比較多的時候，算法的執行效率比較低。

2、KD樹(KD_Tree)

KD_Tree算法中，首先是對訓練數據進行建模，構建KD樹，然后再根據構建好的模型來獲取鄰近樣本數據

KD_Tree是KNN算法中用于計算最近鄰的快速、便捷構建方式

除此之外，還有一些從KD_Tree修改后的求解最鄰近點的算法，比如：Ball Tree、BBF Tree、MVP Tree等

當樣本數據量少的時候，我們可以使用brute這種暴力的方式進行求解最近鄰，即計算到所有樣本的距離。

當樣本量比較大的時候，直接計算所有樣本的距離，工作量有點大，所以在這種情況下，我們可以使用kd tree來快速的計算。

（1）KD數的構建

KD樹采用從m個樣本的n維特征中，分別計算n個特征取值的方差，用方差最大的第 k 維特征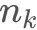作為根節點。對于這個特征，選擇取值的中位數作為樣本的劃分點，對于小于該值的樣本劃分到左子樹，對于大于等于該值的樣本劃分到右子樹，對左右子樹采用同樣的方式找方差最大的特征作為根節點，遞歸即可產生KD樹。

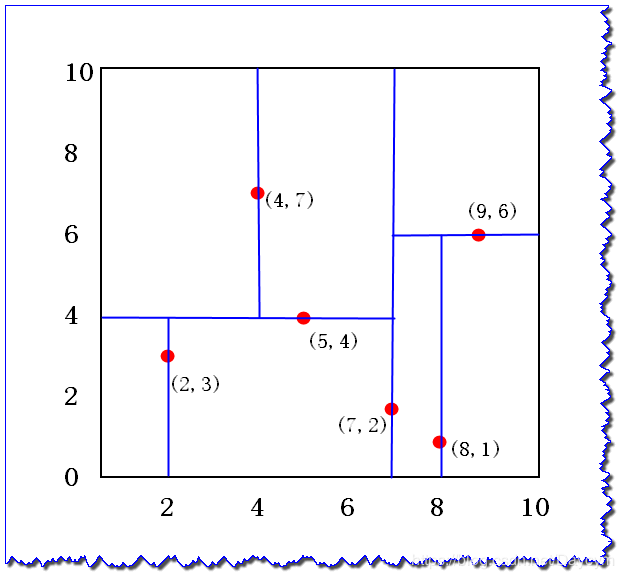
假設二維樣本為：{(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)}，下面我們來構建KD樹：

1、計算每個特征的方差，取方差最大的作為根節點

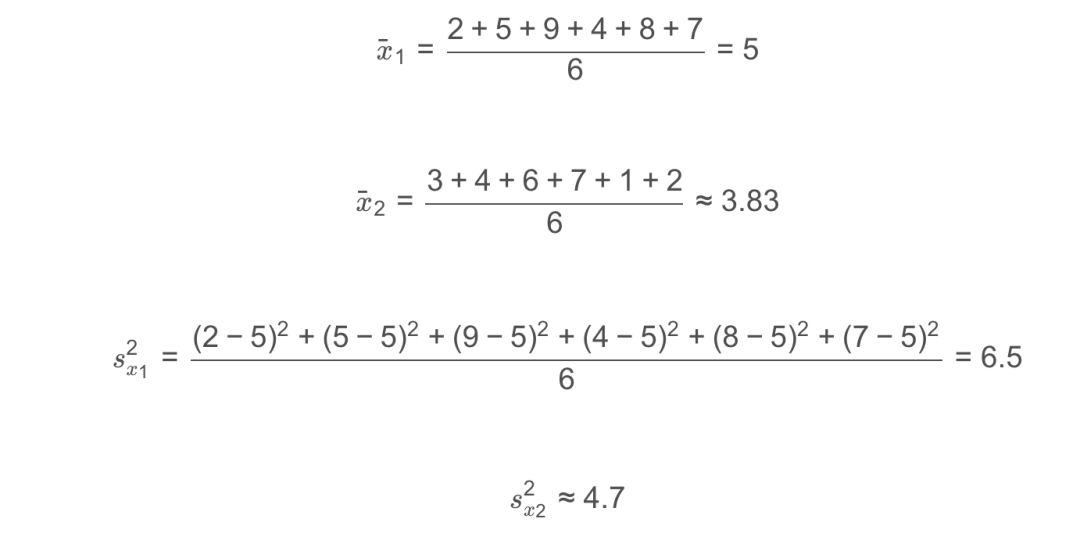
方差表示數據的離散程度，離散程度越大，值越大。因此，選擇第1維特征x1作為根節點。

2、選取中位數作為劃分點

x1取值為2,4,5,7,8,9 2,4,5,7,8,92,4,5,7,8,9中位數取7來劃分，小于該值的放在左子樹，大于該值的放在右子樹

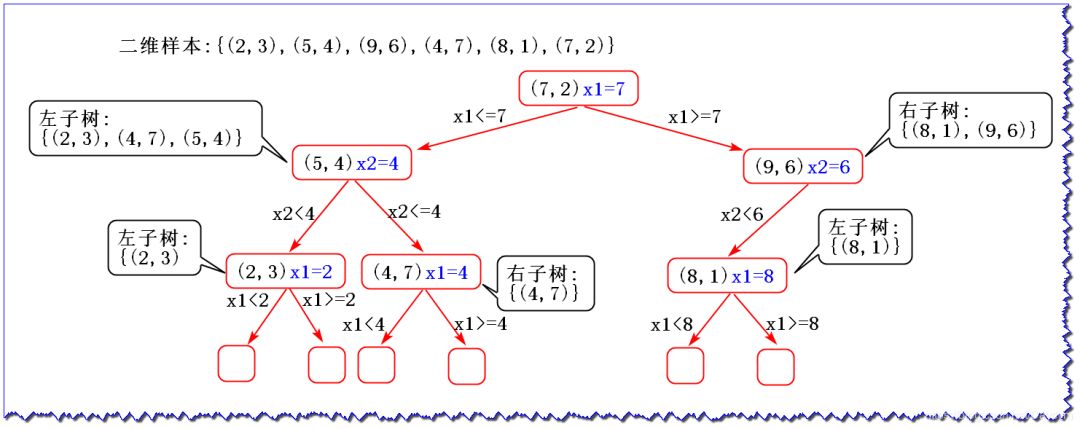
3、特征空間劃分：

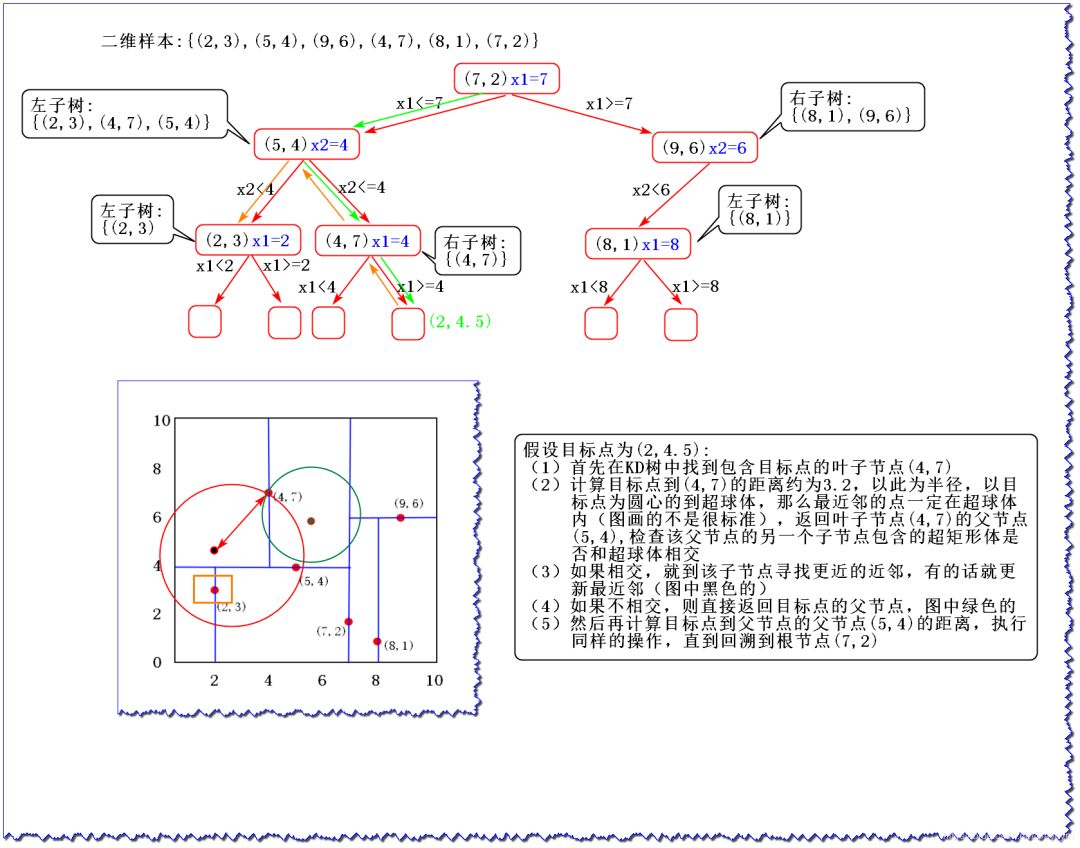
（2）KD tree查找最近鄰

當我們生成KD樹以后，就可以取預測測試集里面的樣本目標點了。

對于一個目標點，我們首先在KD樹里面尋找包含目標點的葉子節點；

以目標點為圓心，以目標點到葉子節點樣本實例的距離為半徑，得到一個超球體，最近鄰的點一定在這個超球體內部；

然后返回葉子節點的父節點，檢查另一個子節點包含的超矩形體是否和超球體相交，如果相交就到這個子節點尋找是否有更加近的近鄰，有點話就更新最近鄰；如果不相交那就直接返回父節點的父節點，在另一個子樹繼續搜索最近鄰；

當回溯到根節點時，算法就結束了，保存最近鄰節點就是最終的最近鄰。

假設要尋找點(2,2.5) (2,2.5)(2,2.5)的最近鄰點：

六、KNN案例

1、鳶尾花數據分類

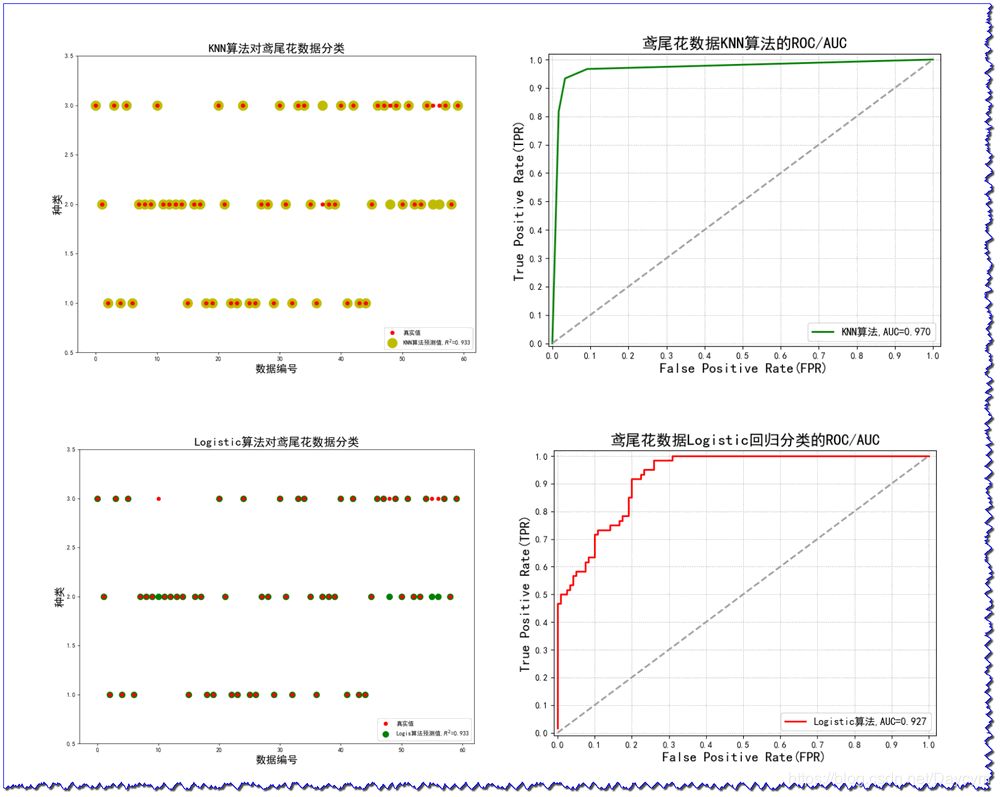
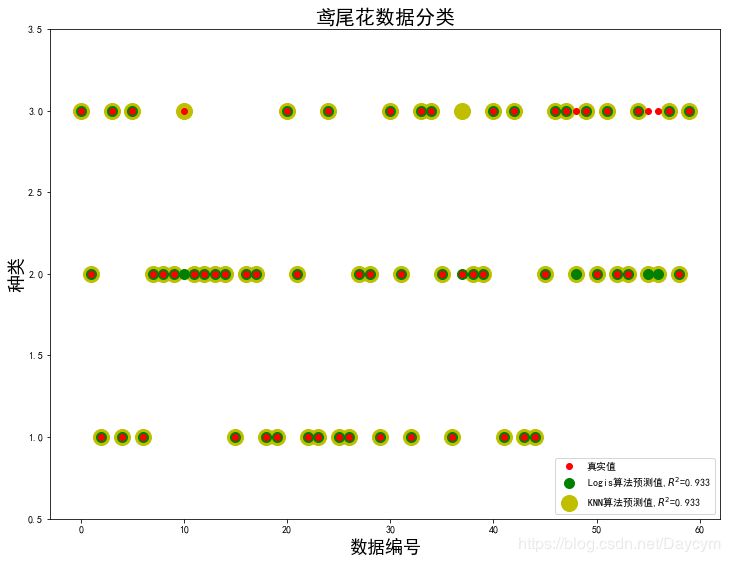
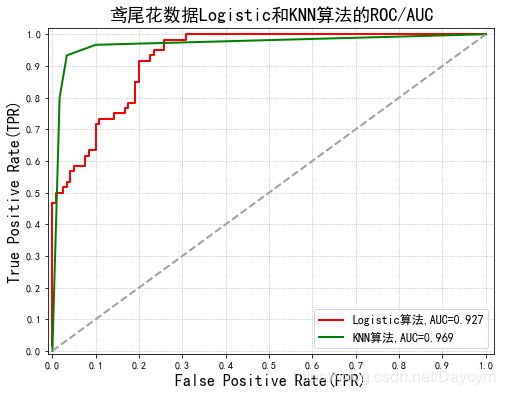
使用Logistic算法和KNN算法對鳶尾花數據進行分類，比較結果；

具體內容在代碼的注釋中有介紹；

畫出下面兩張圖，需要將代碼整合起來，才能畫出來。

代碼可見：https://github.com/Daycym/Machine_Learning；02_Logistic回歸下05_鳶尾花數據分類.py，以及03_KNN目錄下04_鳶尾花數據分類.py。

2、信貸審批

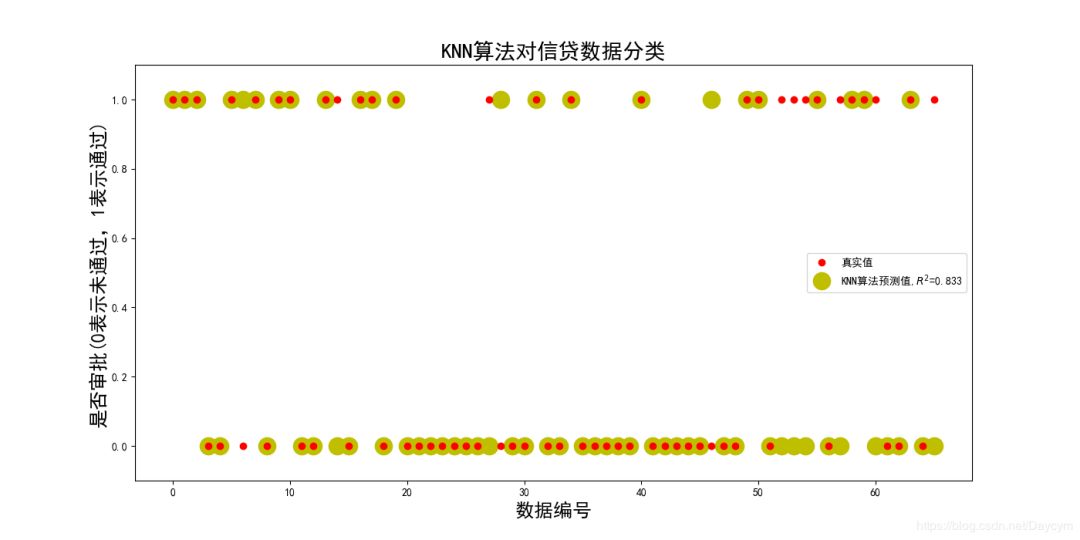
具體內容將在代碼中介紹

代碼可見：https://github.com/Daycym/Machine_Learning；02_Logistic回歸下03_信貸審批.py，以及03_KNN目錄下05_信貸審批.py。

七、總結

本篇主要通過簡單的暴力求解的方式實現KNN算法，有助于理解KNN算法

后面又介紹了KD樹找K個最近鄰，此算法是最快捷的

最后通過sklearn庫下的KNeighborsClassifier實現了兩個案例，來屬性KNN模型的構建