先來看一張本文所有概念的一個思維導圖

為什么要有CPU Cache

隨著工藝的提升最近幾十年CPU的頻率不斷提升，而受制于制造工藝和成本限制，目前計算機的內(nèi)存主要是DRAM并且在訪問速度上沒有質(zhì)的突破。因此，CPU的處理速度和內(nèi)存的訪問速度差距越來越大，甚至可以達到上萬倍。這種情況下傳統(tǒng)的CPU通過FSB直連內(nèi)存的方式顯然就會因為內(nèi)存訪問的等待，導致計算資源大量閑置，降低CPU整體吞吐量。同時又由于內(nèi)存數(shù)據(jù)訪問的熱點集中性，在CPU和內(nèi)存之間用較為快速而成本較高的SDRAM做一層緩存，就顯得性價比極高了。

為什么要有多級CPU Cache

隨著科技發(fā)展，熱點數(shù)據(jù)的體積越來越大，單純的增加一級緩存大小的性價比已經(jīng)很低了。因此，就慢慢出現(xiàn)了在一級緩存(L1 Cache)和內(nèi)存之間又增加一層訪問速度和成本都介于兩者之間的二級緩存(L2 Cache)。下面是一段從What Every Programmer Should Know About Memory中摘錄的解釋：

Soon after the introduction of the cache the system got more complicated. The speed difference between the cache and the main memory increased again, to a point that another level of cache was added, bigger and slower than the first-level cache. Only increasing the size of the first-level cache was not an option for economical rea- sons.

此外，又由于程序指令和程序數(shù)據(jù)的行為和熱點分布差異很大，因此L1 Cache也被劃分成L1i (i for instruction)和L1d (d for data)兩種專門用途的緩存。 下面一張圖可以看出各級緩存之間的響應時間差距，以及內(nèi)存到底有多慢！

什么是Cache Line

Cache Line可以簡單的理解為CPU Cache中的最小緩存單位。目前主流的CPU Cache的Cache Line大小都是64Bytes。假設(shè)我們有一個512字節(jié)的一級緩存，那么按照64B的緩存單位大小來算，這個一級緩存所能存放的緩存?zhèn)€數(shù)就是512/64 = 8個。具體參見下圖：

為了更好的了解Cache Line，我們還可以在自己的電腦上做下面這個有趣的實驗。

下面這段C代碼，會從命令行接收一個參數(shù)作為數(shù)組的大小創(chuàng)建一個數(shù)量為N的int數(shù)組。并依次循環(huán)的從這個數(shù)組中進行數(shù)組內(nèi)容訪問，循環(huán)10億次。最終輸出數(shù)組總大小和對應總執(zhí)行時間。

#include "stdio.h" #include #include long timediff(clock_t t1, clock_t t2) { long elapsed; elapsed = ((double)t2 - t1) / CLOCKS_PER_SEC * 1000; return elapsed;}int main(int argc, char *argv[])#*******{ int array_size=atoi(argv[1]); int repeat_times = 1000000000; long array[array_size]; for(int i=0; i

如果我們把這些數(shù)據(jù)做成折線圖后就會發(fā)現(xiàn)：總執(zhí)行時間在數(shù)組大小超過64Bytes時有較為明顯的拐點（當然，由于博主是在自己的Mac筆記本上測試的，會受到很多其他程序的干擾，因此會有波動）。原因是當數(shù)組小于64Bytes時數(shù)組極有可能落在一條Cache Line內(nèi)，而一個元素的訪問就會使得整條Cache Line被填充，因而值得后面的若干個元素受益于緩存帶來的加速。而當數(shù)組大于64Bytes時，必然至少需要兩條Cache Line，繼而在循環(huán)訪問時會出現(xiàn)兩次Cache Line的填充，由于緩存填充的時間遠高于數(shù)據(jù)訪問的響應時間，因此多一次緩存填充對于總執(zhí)行的影響會被放大，最終得到下圖的結(jié)果：

gcc cache_line_size.c -o cache_line_size編譯，并通過./cache_line_size執(zhí)行。

了解Cache Line的概念對我們程序猿有什么幫助？我們來看下面這個C語言中常用的循環(huán)優(yōu)化例子下面兩段代碼中，第一段代碼在C語言中總是比第二段代碼的執(zhí)行速度要快。具體的原因相信你仔細閱讀了Cache Line的介紹后就很容易理解了。

for(int i = 0; i < n; i++) { ? ?for(int j = 0; j < n; j++) { ? ? ? ?int num; ? ? ? ? ? ?//code ? ? ? ?arr[i][j] = num; ? ?}}for(int i = 0; i < n; i++) { ? ?for(int j = 0; j < n; j++) { ? ? ? ?int num; ? ? ? ? ? ?//code ? ? ? ?arr[j][i] = num; ? ?}}

CPU Cache 是如何存放數(shù)據(jù)的

你會怎么設(shè)計Cache的存放規(guī)則

我們先來嘗試回答一下那么這個問題：

假設(shè)我們有一塊4MB的區(qū)域用于緩存，每個緩存對象的唯一標識是它所在的物理內(nèi)存地址。每個緩存對象大小是64Bytes，所有可以被緩存對象的大小總和（即物理內(nèi)存總大小）為4GB。那么我們該如何設(shè)計這個緩存？

如果你和博主一樣是一個大學沒有好好學習基礎(chǔ)/數(shù)字電路的人的話，會覺得最靠譜的的一種方式就是：Hash表。把Cache設(shè)計成一個Hash數(shù)組。內(nèi)存地址的Hash值作為數(shù)組的Index，緩存對象的值作為數(shù)組的Value。每次存取時，都把地址做一次Hash然后找到Cache中對應的位置操作即可。 這樣的設(shè)計方式在高等語言中很常見，也顯然很高效。因為Hash值得計算雖然耗時(10000個CPU Cycle左右)，但是相比程序中其他操作（上百萬的CPU Cycle）來說可以忽略不計。而對于CPU Cache來說，本來其設(shè)計目標就是在幾十CPU Cycle內(nèi)獲取到數(shù)據(jù)。如果訪問效率是百萬Cycle這個等級的話，還不如到Memory直接獲取數(shù)據(jù)。當然，更重要的原因是在硬件上要實現(xiàn)Memory Address Hash的功能在成本上是非常高的。

為什么Cache不能做成Fully Associative

Fully Associative 字面意思是全關(guān)聯(lián)。在CPU Cache中的含義是：如果在一個Cache集內(nèi)，任何一個內(nèi)存地址的數(shù)據(jù)可以被緩存在任何一個Cache Line里，那么我們成這個cache是Fully Associative。從定義中我們可以得出這樣的結(jié)論：給到一個內(nèi)存地址，要知道他是否存在于Cache中，需要遍歷所有Cache Line并比較緩存內(nèi)容的內(nèi)存地址。而Cache的本意就是為了在盡可能少得CPU Cycle內(nèi)取到數(shù)據(jù)。那么想要設(shè)計一個快速的Fully Associative的Cache幾乎是不可能的。

為什么Cache不能做成Direct Mapped

和Fully Associative完全相反，使用Direct Mapped模式的Cache給定一個內(nèi)存地址，就唯一確定了一條Cache Line。設(shè)計復雜度低且速度快。那么為什么Cache不使用這種模式呢？讓我們來想象這么一種情況：一個擁有1M L2 Cache的32位CPU，每條Cache Line的大小為64Bytes。那么整個L2Cache被劃為了1M/64=16384條Cache Line。我們?yōu)槊織lCache Line從0開始編上號。同時32位CPU所能管理的內(nèi)存地址范圍是2^32=4G，那么Direct Mapped模式下，內(nèi)存也被劃為4G/16384=256K的小份。也就是說每256K的內(nèi)存地址共享一條Cache Line。但是，這種模式下每條Cache Line的使用率如果要做到接近100%，就需要操作系統(tǒng)對于內(nèi)存的分配和訪問在地址上也是近乎平均的。而與我們的意愿相反，為了減少內(nèi)存碎片和實現(xiàn)便捷，操作系統(tǒng)更多的是連續(xù)集中的使用內(nèi)存。這樣會出現(xiàn)的情況就是0-1000號這樣的低編號Cache Line由于內(nèi)存經(jīng)常被分配并使用，而16000號以上的Cache Line由于內(nèi)存鮮有進程訪問，幾乎一直處于空閑狀態(tài)。這種情況下，本來就寶貴的1M二級CPU緩存，使用率也許50%都無法達到。

什么是N-Way Set Associative

為了避免以上兩種設(shè)計模式的缺陷，N-Way Set Associative緩存就出現(xiàn)了。他的原理是把一個緩存按照N個Cache Line作為一組（set），緩存按組劃為等分。這樣一個64位系統(tǒng)的內(nèi)存地址在4MB二級緩存中就劃成了三個部分（見下圖），低位6個bit表示在Cache Line中的偏移量，中間12bit表示Cache組號（set index），剩余的高位46bit就是內(nèi)存地址的唯一id。這樣的設(shè)計相較前兩種設(shè)計有以下兩點好處：

給定一個內(nèi)存地址可以唯一對應一個set，對于set中只需遍歷16個元素就可以確定對象是否在緩存中（Full Associative中比較次數(shù)隨內(nèi)存大小線性增加）

每2^18(256K)*16(way)=4M的連續(xù)熱點數(shù)據(jù)才會導致一個set內(nèi)的conflict（Direct Mapped中512K的連續(xù)熱點數(shù)據(jù)就會出現(xiàn)conflict）

什么N-Way Set Associative的Set段是從低位而不是高位開始的

下面是一段從How Misaligning Data Can Increase Performance 12x by Reducing Cache Misses摘錄的解釋：

The vast majority of accesses are close together, so moving the set index bits upwards would cause more conflict misses. You might be able to get away with a hash function that isn’t simply the least significant bits, but most proposed schemes hurt about as much as they help while adding extra complexity.

由于內(nèi)存的訪問通常是大片連續(xù)的，或者是因為在同一程序中而導致地址接近的（即這些內(nèi)存地址的高位都是一樣的）。所以如果把內(nèi)存地址的高位作為set index的話，那么短時間的大量內(nèi)存訪問都會因為set index相同而落在同一個set index中，從而導致cache conflicts使得L2, L3 Cache的命中率低下，影響程序的整體執(zhí)行效率。

了解N-Way Set Associative的存儲模式對我們有什么幫助

了解N-Way Set的概念后，我們不難得出以下結(jié)論：2^(6Bits + 12Bits )=2^18=256K。即在連續(xù)的內(nèi)存地址中每256K都會出現(xiàn)一個處于同一個Cache Set中的緩存對象。也就是說這些對象都會爭搶一個僅有16個空位的緩存池（16-Way Set）。而如果我們在程序中又使用了所謂優(yōu)化神器的“內(nèi)存對齊”的時候，這種爭搶就會越發(fā)增多。效率上的損失也會變得非常明顯。具體的實際測試我們可以參考：How Misaligning Data Can Increase Performance 12x by Reducing Cache Misses一文。 這里我們引用一張Gallery of Processor Cache Effects中的測試結(jié)果圖，來解釋下內(nèi)存對齊在極端情況下帶來的性能損失。

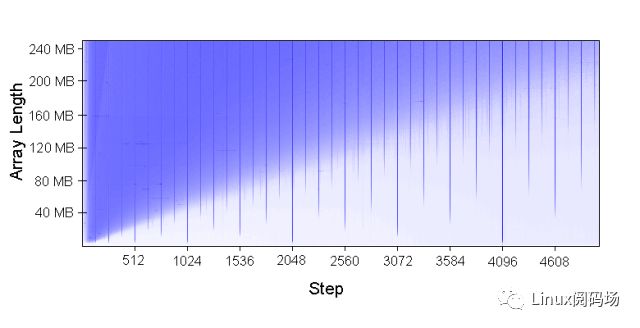
該圖實際上是我們上文中第一個測試的一個變種。縱軸表示了測試對象數(shù)組的大小。橫軸表示了每次數(shù)組元素訪問之間的index間隔。而圖中的顏色表示了響應時間的長短，藍色越明顯的部分表示響應時間越長。從這個圖我們可以得到很多結(jié)論。當然這里我們只對內(nèi)存帶來的性能損失感興趣。有興趣的讀者也可以閱讀原文分析理解其他從圖中可以得到的結(jié)論。

從圖中我們不難看出圖中每1024個步進，即每1024*4即4096Bytes，都有一條特別明顯的藍色豎線。也就是說，只要我們按照4K的步進去訪問內(nèi)存(內(nèi)存根據(jù)4K對齊），無論熱點數(shù)據(jù)多大它的實際效率都是非常低的！按照我們上文的分析，如果4KB的內(nèi)存對齊，那么一個240MB的數(shù)組就含有61440個可以被訪問到的數(shù)組元素；而對于一個每256K就會有set沖突的16Way二級緩存，總共有256K/4K=64個元素要去爭搶16個空位，總共有61440/64=960個這樣的元素。那么緩存命中率只有1%，自然效率也就低了。

Cache淘汰策略

在文章的最后我們順帶提一下CPU Cache的淘汰策略。常見的淘汰策略主要有LRU和Random兩種。通常意義下LRU對于Cache的命中率會比Random更好，所以CPU Cache的淘汰策略選擇的是LRU。當然也有些實驗顯示在Cache Size較大的時候Random策略會有更高的命中率

總結(jié)

CPU Cache對于程序猿是透明的，所有的操作和策略都在CPU內(nèi)部完成。但是，了解和理解CPU Cache的設(shè)計、工作原理有利于我們更好的利用CPU Cache，寫出更多對CPU Cache友好的程序。