在傳統(tǒng)的神經網絡中，比如多層感知機（MLP），其輸入通常是一個特征向量。需要人工設計特征，然后將用這些特征計算的值組成特征向量。在過去幾十年的經驗來看，人工找的特征并不總是好用。有時多了，有時少了，有時選的特征根本就不起作用（真正起作用的特征在浩瀚的未知里）。這就是為啥過去幾十年神經網絡一直被SVM等完虐的原因。

如果有人說，任何特征都是從圖像中提取的。那如果把整幅圖像作為特征來訓練神經網絡不就行了嘛，那肯定不會有任何的信息丟失！額，先不說一幅圖像有多少冗余信息，單說這數據量就嚇死了！

假如有一幅1000*1000的圖像，如果把整幅圖像作為向量，則向量的長度為1000000（10^6）。在假如隱含層神經元的個數和輸入一樣，也是1000000；那么，輸入層到隱含層的參數數據量有10^12，媽呀，什么樣的機器能訓練這樣的網絡呢。所以，我們還得降低維數，同時得以整幅圖像為輸入（人類實在找不到好的特征了）。于是，牛逼的卷積來了。接下來看看卷積都干了些啥。

局部感知：

卷積神經網絡有兩種神器可以降低參數數目，第一種神器叫做局部感知野。一般認為人對外界的認知是從局部到全局的，而圖像的空間聯系也是局部的像素聯系較為緊密，而距離較遠的像素相關性則較弱。因而，每個神經元其實沒有必要對全局圖像進行感知，只需要對局部進行感知，然后在更高層將局部的信息綜合起來就得到了全局的信息。網絡部分連通的思想，也是受啟發(fā)于生物學里面的視覺系統(tǒng)結構。視覺皮層的神經元就是局部接受信息的（即這些神經元只響應某些特定區(qū)域的刺激）。

如下圖所示：左圖為全連接，右圖為局部連接。

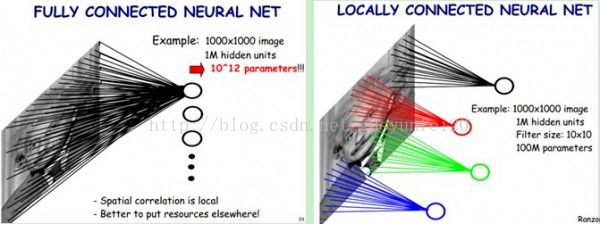
在上右圖中，假如每個神經元只和10×10個像素值相連，那么權值數據為1000000×100個參數，減少為原來的千分之一。而那10×10個像素值對應的10×10個參數，其實就相當于卷積操作。

權值共享：

但其實這樣的話參數仍然過多，那么就啟動第二級神器，即權值共享。在上面的局部連接中，每個神經元都對應100個參數，一共1000000個神經元，如果這1000000個神經元的100個參數都是相等的，那么參數數目就變?yōu)?00了。

怎么理解權值共享呢？

我們可以這100個參數（也就是卷積操作）看成是提取特征的方式，該方式與位置無關。這其中隱含的原理則是：圖像的一部分的統(tǒng)計特性與其他部分是一樣的。這也意味著我們在這一部分學習的特征也能用在另一部分上，所以對于這個圖像上的所有位置，我們都能使用同樣的學習特征。

更直觀一些，當從一個大尺寸圖像中隨機選取一小塊，比如說 8×8 作為樣本，并且從這個小塊樣本中學習到了一些特征，這時我們可以把從這個 8×8 樣本中學習到的特征作為探測器，應用到這個圖像的任意地方中去。特別是，我們可以用從 8×8 樣本中所學習到的特征跟原本的大尺寸圖像作卷積，從而對這個大尺寸圖像上的任一位置獲得一個不同特征的激活值。

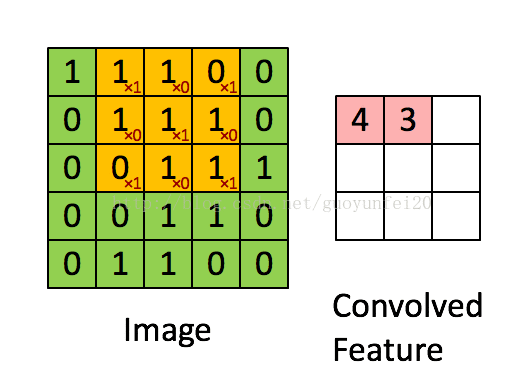
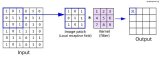
如下圖所示，展示了一個3*3的卷積核在5*5的圖像上做卷積的過程。每個卷積都是一種特征提取方式，就像一個篩子，將圖像中符合條件（激活值越大越符合條件）的部分篩選出來。

多卷積核：

上面所述只有100個參數時，表明只有1個100*100的卷積核，顯然，特征提取是不充分的，我們可以添加多個卷積核，比如32個卷積核，可以學習32種特征。在有多個卷積核時，如下圖所示：

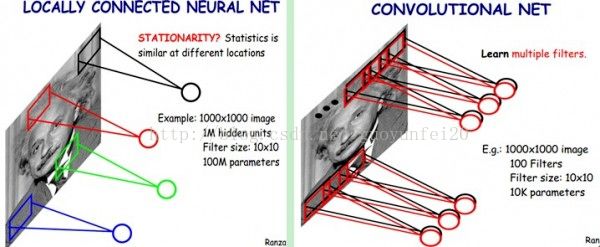
上圖右，不同顏色表明不同的卷積核。每個卷積核都會將圖像生成為另一幅圖像。比如兩個卷積核就可以將生成兩幅圖像，這兩幅圖像可以看做是一張圖像的不同的通道。如下圖所示：

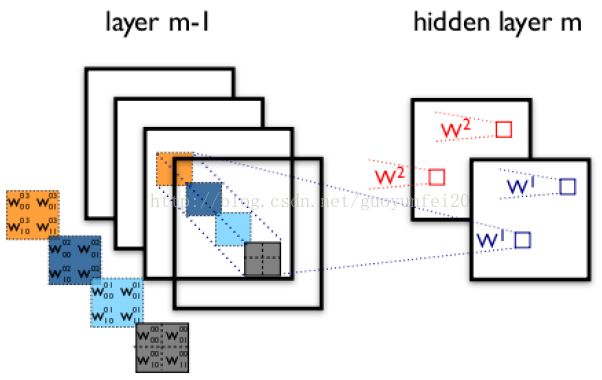
池化（down-samplin）：

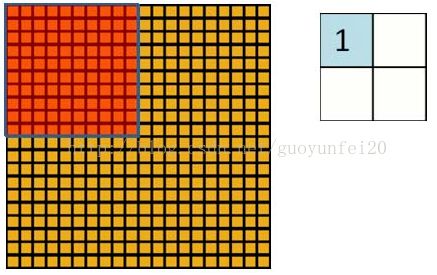
在通過卷積獲得了特征 (features) 之后，下一步我們希望利用這些特征去做分類。理論上講，人們可以用所有提取得到的特征去訓練分類器，例如 softmax 分類器，但這樣做面臨計算量的挑戰(zhàn)。例如：對于一個 96X96 像素的圖像，假設我們已經學習得到了400個定義在8X8輸入上的特征，每一個特征和圖像卷積都會得到一個 (96 ? 8 + 1) × (96 ? 8 + 1) = 7921 維的卷積特征，由于有 400 個特征，所以每個樣例 (example) 都會得到一個 7921 × 400 = 3,168,400 維的卷積特征向量。學習一個擁有超過 3 百萬特征輸入的分類器十分不便，并且容易出現過擬合 (over-fitting)。

為了解決這個問題，首先回憶一下，我們之所以決定使用卷積后的特征是因為圖像具有一種“靜態(tài)性”的屬性，這也就意味著在一個圖像區(qū)域有用的特征極有可能在另一個區(qū)域同樣適用。因此，為了描述大的圖像，一個很自然的想法就是對不同位置的特征進行聚合統(tǒng)計，例如，人們可以計算圖像一個區(qū)域上的某個特定特征的平均值 (或最大值)。這些概要統(tǒng)計特征不僅具有低得多的維度 (相比使用所有提取得到的特征)，同時還會改善結果(不容易過擬合)。這種聚合的操作就叫做池化 (pooling)，有時也稱為平均池化或者最大池化 (取決于計算池化的方法)。

多卷積層：

在實際應用中，往往使用多層卷積，然后再使用全連接層進行訓練，多層卷積的目的是一層卷積學到的特征往往是局部的，層數越高，學到的特征就越全局化。

到此，基本上就把CNN中的卷積說全了！