深度學(xué)習(xí)在圖像分類，機(jī)器翻譯等領(lǐng)域都展示了其強(qiáng)大的能力，但是在因果推理方面，深度學(xué)習(xí)依然是短板。圖神經(jīng)網(wǎng)絡(luò)在因果推理方面有巨大的潛力，有望成為 AI 的下一個(gè)拐點(diǎn)。本文將深入了解圖神經(jīng)網(wǎng)絡(luò)背后的原理和其強(qiáng)大的表征能力。

圖神經(jīng)網(wǎng)絡(luò)（GNNs）廣泛應(yīng)用于圖的表征學(xué)習(xí)，其遵循鄰域聚合框架，通過(guò)遞歸聚合和轉(zhuǎn)換相鄰節(jié)點(diǎn)的特征向量來(lái)計(jì)算節(jié)點(diǎn)的表征向量。已經(jīng)提出了許多 GNN 的變體，并在節(jié)點(diǎn)和圖形分類任務(wù)上取得比較好的結(jié)果。然而，盡管 GNN 使圖形表征學(xué)習(xí)發(fā)生了革命性的變化，但是，對(duì)其表示屬性和局限性的理解還很有限。

本文譯介自MIT、斯坦福大學(xué)的ICLR-19論文：HOW POWERFUL ARE GRAPH NEURAL NETWORKS。

論文地址：https://arxiv.org/pdf/1810.00826.pdf

論文提出了一個(gè)在分析 GNN 捕獲不同圖結(jié)構(gòu)表現(xiàn)力的理論框架。本論文描述了各種流行的 GNN 變體的判別能力，如 Graph Convolutional Networks (圖卷積神經(jīng)網(wǎng)絡(luò)) 和 GraphSAGE，并表明他們無(wú)法學(xué)會(huì)區(qū)分某些簡(jiǎn)單的圖結(jié)構(gòu)。然后，本論文開(kāi)發(fā)了一個(gè)簡(jiǎn)單的體系結(jié)構(gòu)，可以證明其在 GNNs 類中是最具表現(xiàn)力的，并且它和 Weisfeiler-Lehman (圖同構(gòu)測(cè)試) 方法一樣強(qiáng)大。在許多圖分類基準(zhǔn)測(cè)試上，通過(guò)經(jīng)驗(yàn)驗(yàn)證了該理論發(fā)現(xiàn)，并證明本論文的模型達(dá)到了最佳的性能。

介紹

學(xué)習(xí)圖結(jié)構(gòu)數(shù)據(jù)，例如：分子、社會(huì)、生物和金融網(wǎng)絡(luò)等，需要有效的表征圖的結(jié)構(gòu)。最近，研究者們對(duì)使用Graph Neural Network (GNN)方法來(lái)對(duì)圖進(jìn)行表征學(xué)習(xí)產(chǎn)生了極大的興趣。GNN 大部分都遵循循環(huán)遞歸鄰域聚合（或者消息傳遞）的模式，其中每個(gè)節(jié)點(diǎn)聚合其相鄰節(jié)點(diǎn)的特征向量以計(jì)算其新的特征向量。在 k 輪聚合迭代后，通過(guò)其轉(zhuǎn)換的特征向量來(lái)表示該節(jié)點(diǎn)，該向量捕獲節(jié)點(diǎn)的 k-hop 網(wǎng)絡(luò)鄰節(jié)點(diǎn)的結(jié)構(gòu)信息。然后，可以通過(guò) pooling 來(lái)獲得整個(gè)圖結(jié)構(gòu)的表征，例如對(duì)圖中所有節(jié)點(diǎn)的表征向量求和。許多基于不同 neighborhod aggregation 的 GNN 變體和 graph-level 的 pooling scheme 已經(jīng)被許多學(xué)者提出。

根據(jù)經(jīng)驗(yàn)，這些 GNNs 已經(jīng)在許多任務(wù)中達(dá)到最佳的性能，如節(jié)點(diǎn)分類，鏈接預(yù)測(cè)和圖分類。然而，新 GNN 的設(shè)計(jì)主要是基于經(jīng)驗(yàn)直覺(jué)，啟發(fā)式和實(shí)驗(yàn)試錯(cuò)。對(duì)于 GNN 的性質(zhì)和局限性，目前理論層面的解釋還比較少。GNN 的表征能力的正式分析還是有限的。

本論文提出了一個(gè)分析 GNN 表征能力的理論框架。從形式上描述了不同 GNN 變體在學(xué)習(xí)表征和區(qū)分各種圖結(jié)構(gòu)方面的表現(xiàn)力。該框架是受 GNNs 和 WL 測(cè)試（Weisfeiler-Lehman 圖同構(gòu)測(cè)試）緊密聯(lián)系的啟發(fā)，WL 測(cè)試是以其強(qiáng)大的區(qū)分各種圖結(jié)構(gòu)能力而聞名。與 GNNs 相似，WL 測(cè)試通過(guò)聚合給定節(jié)點(diǎn)的鄰近節(jié)點(diǎn)的特征向量迭代更新其特征向量。WL 測(cè)試的強(qiáng)大之處是其注入聚合（injective aggregation）更新，它映射不同節(jié)點(diǎn)的鄰近節(jié)點(diǎn)到不同的特征向量。主要觀點(diǎn)是，如果 GNN 的聚合模式具有高度的表現(xiàn)力和能夠?yàn)樽⑷牒瘮?shù)建模的話，它就同 WL 測(cè)試一樣具有強(qiáng)大的區(qū)分能力。

為了數(shù)學(xué)形式化上述觀點(diǎn)，首先抽象出一個(gè)節(jié)點(diǎn)的鄰近節(jié)點(diǎn)的特征向量作為多重集，該集合中可能有重復(fù)元素。然后，在 GNNS 中的領(lǐng)域聚合（neighbor aggregation）可以抽象為多集上的函數(shù)。我們嚴(yán)格學(xué)習(xí)不同多集函數(shù)的變體，并從理論上描述其識(shí)別能力，即不同的聚合函數(shù)可以區(qū)分不同的多重集。越具有區(qū)分力的多重集函數(shù)，GNN 的潛在表征能力就越強(qiáng)。

本論文的主要結(jié)果總結(jié)如下：

1）我們發(fā)現(xiàn)在區(qū)分圖結(jié)構(gòu)方面，GNN 跟 WL 測(cè)試能力一樣強(qiáng)大。

2）我們發(fā)現(xiàn)在建立領(lǐng)域聚合（neighbor aggregation）和圖池函數(shù)（graph pooling）的情況下，得到的 GNN 和 WL 測(cè)試一樣強(qiáng)大。

3）我們識(shí)別無(wú)法通過(guò)流行的 GNN 變體區(qū)分的圖結(jié)構(gòu)，例如 GCN（Kipf＆Welling，2017）和 GraphSAGE（Hamilton 等，2017a），并且我們對(duì)基于 GNN 模型可以捕獲的各種圖結(jié)構(gòu)進(jìn)行了精確的描述。

4）我們開(kāi)發(fā)了一個(gè)簡(jiǎn)單的神經(jīng)網(wǎng)絡(luò)架構(gòu)，圖同構(gòu)網(wǎng)絡(luò)（Graph Isomorphism Network）GIN，并證明其判別 / 表征能力等同于 WL 測(cè)試。

在圖分類數(shù)據(jù)集上，通過(guò)實(shí)驗(yàn)驗(yàn)證我們的理論，其中 GNN 的表達(dá)能力對(duì)于捕獲圖結(jié)構(gòu)至關(guān)重要。特別是，我們對(duì)基于各種聚合函數(shù)的 GNN 性能進(jìn)行了對(duì)比。我們的結(jié)果證實(shí)了最強(qiáng)大的 GNN（我們的圖同構(gòu)網(wǎng)絡(luò) GIN）具有很強(qiáng)的表征能力，可以近乎完美的擬合訓(xùn)練數(shù)據(jù)，然而較弱的 GNN 變體有嚴(yán)重的欠擬合問(wèn)題。此外，在許多圖分類的基準(zhǔn)測(cè)試集上，它的表征能力和性能優(yōu)于其他的 GNNs。

預(yù)備知識(shí)

首先，我們總結(jié)一些常見(jiàn)的 GNN 模型，順便介紹一下相關(guān)數(shù)學(xué)符號(hào)的含義。假設(shè) G = (V, E) 表示一個(gè)圖，圖的節(jié)點(diǎn)向量用 X (v) 表示，其中，v ∈ V 。有兩個(gè)比較感興趣的任務(wù)：（1）節(jié)點(diǎn)分類，其中每個(gè)節(jié)點(diǎn) v ∈ V 都有一個(gè)相關(guān)的標(biāo)簽 y (v)，目標(biāo)是學(xué)習(xí)節(jié)點(diǎn) v 的表征向量 h (v)，節(jié)點(diǎn) v 的標(biāo)簽可以被函數(shù) y (v)=f (h (v)) 所預(yù)測(cè)。（2）圖分類，其中給定一組圖 {G1, ..., GN }? G 及其標(biāo)簽 {y1, ..., yN } ? Y，我們的目標(biāo)是學(xué)習(xí)一個(gè)表征向量 h (G)，它有助于預(yù)測(cè)整個(gè)圖的標(biāo)簽 y (G) = g (h (G))。

圖神經(jīng)網(wǎng)絡(luò)

GNNs 利用圖結(jié)構(gòu)和節(jié)點(diǎn)特征 X (v) 來(lái)學(xué)習(xí)一個(gè)節(jié)點(diǎn)的表征向量 h (v)，或者整個(gè)圖的表征向量 h (G)。

新式的 GNNs 都遵循領(lǐng)域聚合（neighborhood aggregation）策略，其中我們通過(guò)聚合它的鄰近節(jié)點(diǎn)的表征向量來(lái)迭代更新節(jié)點(diǎn)的表征向量。在 k 次迭代后，節(jié)點(diǎn)的表征可以在它的 k-hop 網(wǎng)絡(luò)鄰居中捕獲結(jié)構(gòu)信息。形式上，GNN 的第 k 層是：

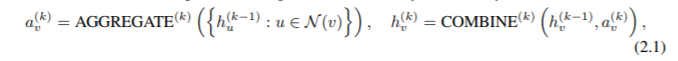
其中，h {k}(v) 是節(jié)點(diǎn) v 在第 k 的迭代 / 層的特征向量。我們初始化 h {0}(v)=X (v)，N (v) 是與 v 節(jié)點(diǎn)鄰近的一組節(jié)點(diǎn)。在 GNNs 中選擇函數(shù) AGGREGATE {k}(?) 和 COMBINE {k}(?) 非常關(guān)鍵。已經(jīng)提出了許多用于聚合的體系結(jié)構(gòu)。在 GraphSAGE 的 pooling 變體（Hamilton et al., 2017a），AGGREGATE 函數(shù)形式如下：

其中，W 是可以學(xué)習(xí)的矩陣，MAX 表示一個(gè) element-wise 的 max-pooling。在 GraphSAGE 的 COMBINE 步是一個(gè)線性映射的連接 W?[h {k-1}(v)|a {k}(v)]。在圖卷積網(wǎng)絡(luò)中（GCN）(Kipf & Welling, 2017)，element-wise 的 mean pooling 被替代，AGGREGATE 和 COMBINE 步集成在一體如下：

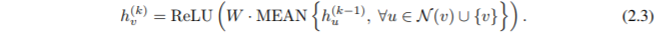
許多其他的 GNNs 可以類似的表示為 Eq. 2.1 (Xu et al., 2018; Gilmer et al., 2017)。

對(duì)于節(jié)點(diǎn)分類問(wèn)題，最后一次迭代的節(jié)點(diǎn)表征向量 h {K}(v) 用來(lái)做預(yù)測(cè)。對(duì)于圖分類問(wèn)題，READOUT 函數(shù)從最后一次迭代中聚合節(jié)點(diǎn)特征來(lái)獲取整個(gè)圖的表征向量 h (G)：

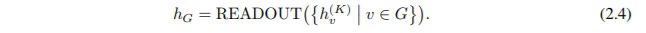
READOUT 函數(shù)可以是一個(gè)簡(jiǎn)單的置換不變函數(shù)，例如求和或者 graph-level 級(jí)別的 pooling 函數(shù) (Ying et al., 2018; Zhang et al., 2018)。

Weisfeiler-Lehman 測(cè)試

圖同構(gòu)問(wèn)題指的是驗(yàn)證兩個(gè)圖在拓?fù)浣Y(jié)構(gòu)上是否相同。這是一個(gè)具有挑戰(zhàn)性的問(wèn)題：因?yàn)楝F(xiàn)在很難知道計(jì)算的時(shí)間復(fù)雜度。WL（Weisfeiler-Lehman）測(cè)試是一種非常有效的一測(cè)試圖同構(gòu)的方法，它可以區(qū)分各種圖。

在 1 維的情況下，它類似于在 GNN 中的領(lǐng)域聚合。假設(shè)每個(gè)節(jié)點(diǎn)都有一個(gè)分類標(biāo)簽，WL 測(cè)試（1）迭代聚合節(jié)點(diǎn)標(biāo)簽和他們的鄰近節(jié)點(diǎn)，（2）將聚合的標(biāo)簽 hash 成唯一的新標(biāo)簽。如果在某些迭代中兩個(gè)圖的節(jié)點(diǎn)標(biāo)簽不同，則該算法判定它們是不同的。

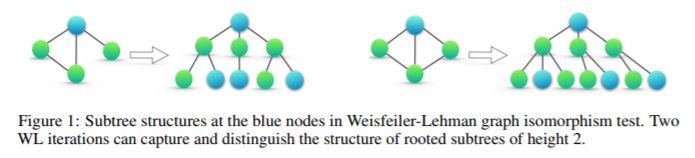
基于 WL 試驗(yàn)，Shervashidze 等人（2011）提出了 WL 子樹內(nèi)核來(lái)測(cè)量圖之間的相似性。內(nèi)核使用在 WL 測(cè)試不同迭代中的節(jié)點(diǎn)標(biāo)簽計(jì)數(shù)作為圖的特征向量。直觀的來(lái)看，在 WL 測(cè)試的第 k 次迭代中，一個(gè)節(jié)點(diǎn)的標(biāo)簽表征該根節(jié)點(diǎn)的高度為 k 的子樹結(jié)構(gòu)（Figure 1）。因此，WL 子樹所考慮的圖的特征本質(zhì)上是圖中不同根子樹的計(jì)數(shù)。

理論框架：概述

我們首先概述了分析 GNNs 表達(dá)能力的框架。GNN 遞歸地更新每個(gè)節(jié)點(diǎn)的特征向量，以捕獲其周圍其他節(jié)點(diǎn)的網(wǎng)絡(luò)結(jié)構(gòu)和特征，即其根子樹結(jié)構(gòu)（圖 1）。在本文中，我們假設(shè)節(jié)點(diǎn)輸入特征是一個(gè)宇宙內(nèi)可數(shù)的數(shù)。對(duì)于有限圖，我們可以遞歸地證明在任何固定模型的深層節(jié)點(diǎn)特征向量也是一個(gè)宇宙內(nèi)可數(shù)的數(shù)。為了簡(jiǎn)化符號(hào)，我們可以為每個(gè)特征向量分配一個(gè)唯一的標(biāo)簽∈{a，b，c……}。 然后，一組相鄰節(jié)點(diǎn)的特征向量形成多重集：同一元素可以出現(xiàn)多次，因?yàn)椴煌墓?jié)點(diǎn)可以具有相同的特征向量。

多重集定義：多重集是集合的一個(gè)廣義概念，它允許其元素有多個(gè)實(shí)例。更正式地講，多重集是一個(gè)二元組 X =（S，m），其中 S 是由其不同元素組成的 X 的基礎(chǔ)集合，而 m：S→N (≥1) 給出了元素的多樣性。

為了分析 GNN 的表達(dá)能力，我們分析了 GNN 何時(shí)將兩個(gè)節(jié)點(diǎn)映射到嵌入空間中的相同位置。直觀地說(shuō)，最強(qiáng)大的 GNN 僅當(dāng)兩個(gè)節(jié)點(diǎn)具有相同的子樹結(jié)構(gòu)，并且在對(duì)應(yīng)的節(jié)點(diǎn)上具有相同的特征時(shí)，才會(huì)將它們映射到相同的位置。由于子樹結(jié)構(gòu)是通過(guò)節(jié)點(diǎn)鄰域遞歸定義的（圖 1），因此當(dāng) GNN 將兩個(gè)鄰域映射到相同的嵌入時(shí)，我們可以遞歸地減少我們的分析。最強(qiáng)大的 GNN 永遠(yuǎn)不會(huì)將兩個(gè)不同的鄰域（即，特征向量的多重集）映射到相同的位置。這意味著它的聚合方案是單射的。 因此，我們將 GNN 的聚合方案抽象為其神經(jīng)網(wǎng)絡(luò)可以表示的多重集合上的一類函數(shù)，并分析它們是否能夠表示單射的多重集函數(shù)。

接下來(lái)，我們使用這種推理開(kāi)發(fā)一個(gè)最強(qiáng)大的 GNN。 在第 5 節(jié)中，我們研究了流行的 GNN 變體，并發(fā)現(xiàn)它們的聚合方案本質(zhì)上不是單射的，因此功能較弱，但它們可以捕獲圖形的其他有趣屬性。

構(gòu)建強(qiáng)大的圖神經(jīng)網(wǎng)絡(luò)

理想情況下，GNN 能夠（1）通過(guò)將它們映射到嵌入空間中的不同位置來(lái)區(qū)分不同的圖結(jié)構(gòu)，以及（2）在嵌入空間中捕獲它們的結(jié)構(gòu)相似性。在本文中，我們主要關(guān)注第一部分，我們將簡(jiǎn)要討論第二部分。然而，將不同的圖映射到不同的嵌入空間的能力意味著可以解決圖同構(gòu)問(wèn)題。

在我們的分析中，通過(guò)一個(gè)稍微弱一點(diǎn)的標(biāo)準(zhǔn)來(lái)描述 GNN 的表達(dá)能力：魏斯費(fèi)勒 - 雷曼（WL）圖同構(gòu)測(cè)試，除少數(shù)特例外，該測(cè)試通常工作得很好，特別是規(guī)則圖（Cai 等人，1992；Douglas，2011；Evdokimov&Ponomarenko，1999）。

引理 2. 設(shè) G1 和 G2 為任何非同構(gòu)圖。如果一個(gè)圖神經(jīng)網(wǎng)絡(luò) A: G → R (d) 遵循領(lǐng)域聚合方案，將 G1 和 G2 映射到不同的嵌入，Weisfeiler-Lehman 圖同構(gòu)檢驗(yàn)也判定 G1 和 G2 不是同構(gòu)的。

因此，在區(qū)分不同圖方面任何基于聚合的 GNN 都至多與 WL 測(cè)試一樣強(qiáng)大。一個(gè)自然的問(wèn)題是，在原則上是否存與 WL 測(cè)試一樣強(qiáng)大的 GNN？ 我們?cè)诙ɡ?3 中得到的答案是肯定的：如果鄰居聚合和圖池化函數(shù)是單射的，那么得到的 GNN 就像 WL 測(cè)試一樣強(qiáng)大。

定理 3.設(shè) A：G→R (d) 是一個(gè)遵循鄰域聚合方案的 GNN。 通過(guò)足夠的迭代，如果滿足以下條件，則 A 可以將通過(guò) Weisfeiler-Lehman 測(cè)試的圖 G1 和 G2 為非同構(gòu)圖映射到不同的嵌入：

a) A 每次迭代聚合更新節(jié)點(diǎn)特征向量

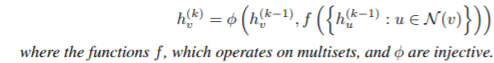
b）A 的圖級(jí)別的 readout 函數(shù)，運(yùn)行在節(jié)點(diǎn)特征的多重集上｛h (k)(v)｝，是一個(gè)單射函數(shù)。

在可數(shù)集上，單射性很好地描述了一個(gè)函數(shù)是否保留了輸入的區(qū)別性。在不可數(shù)集上，節(jié)點(diǎn)特征是連續(xù)的，內(nèi)射性和判別性的概念被 “削弱”。在本文中，我們假設(shè)輸入節(jié)點(diǎn)特征來(lái)自可數(shù)集。鑒于輸入節(jié)點(diǎn)特征的可計(jì)數(shù)性假設(shè)，人們可能會(huì)問(wèn)，GNN 更深層的節(jié)點(diǎn)特征的可數(shù)性是否仍然適用？ 引理 4 表示是，即可數(shù)性可以跨層傳播。

引理 4. 假設(shè)輸入特征空間 X 是可數(shù)的，g (k) 是由 GNN 的第 k 層參數(shù)化的函數(shù)，k=1,..,L。其中，g (1) 被定義在有限多重集 X ? X 上，g (k) 的范圍，節(jié)點(diǎn)的隱含特征 h {k}(v) 空間，在 k=1,...,L 都是可數(shù)的。

在這里，除了區(qū)分不同的圖之外，還值得討論 GNN 的一個(gè)重要好處，也就是說(shuō)，捕捉圖結(jié)構(gòu)的相似性。注意，WL 測(cè)試中的節(jié)點(diǎn)特征向量本質(zhì)上是一種獨(dú)熱編碼（one-hot 編碼），因此不能捕獲子樹之間的相似性。相反，滿足定理 3 標(biāo)準(zhǔn)的 GNN，通過(guò)學(xué)習(xí)將子樹嵌入低維空間來(lái)推廣 WL 測(cè)試。這使得 GNN 不僅可以區(qū)分不同的結(jié)構(gòu)，而且可以學(xué)習(xí)將相似的圖結(jié)構(gòu)映射到相似的嵌入，并捕獲圖結(jié)構(gòu)之間的依賴關(guān)系。捕捉節(jié)點(diǎn)標(biāo)簽的結(jié)構(gòu)相似性對(duì)泛化有幫助，特別是在不同的圖中當(dāng)子樹的共現(xiàn)稀疏或存在噪聲邊和節(jié)點(diǎn)特征時(shí)（Yanardag 和 Vishwanathan，2015）。

圖異構(gòu)網(wǎng)絡(luò)（GIN）

接下來(lái)，我們開(kāi)發(fā)了一個(gè)可證明滿足定理 3 中條件的模型，從而推廣了 WL 測(cè)試。 我們將結(jié)果體系結(jié)構(gòu)命名為 Graph Isomorphism Network（GIN）。為了模擬領(lǐng)域聚合的單射多重集函數(shù)，我們發(fā)展了一個(gè) “深多重集” 的理論，即用神經(jīng)網(wǎng)絡(luò)參數(shù)化通用多重集函數(shù)。我們的下一個(gè)引理表明，求和聚合器可以代表多重集合的單射，事實(shí)上，是多重集上的通用函數(shù)。

引理 5. 定義如下：

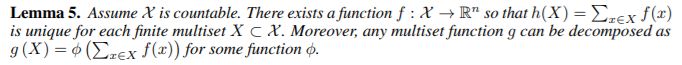
該引理擴(kuò)展了設(shè)置 (Zaheer et al., 2017) 從集合到多重集。深多重集和集合之間的一個(gè)重要區(qū)別是某些單射集合函數(shù)，例如均值聚合器，不是多重集函數(shù)。利用引理 5 中通用多重集函數(shù)的建模機(jī)制作為構(gòu)建塊，現(xiàn)在我們提出一種聚合方案，可以表示節(jié)點(diǎn)對(duì)和其鄰居的多重集合上的通用函數(shù)，從而滿足定理 3a 中的單射性條件。 我們的下一個(gè)推論在許多這樣的聚合方案中提供了簡(jiǎn)單而具體的公式。

推論 6. 定義如下：

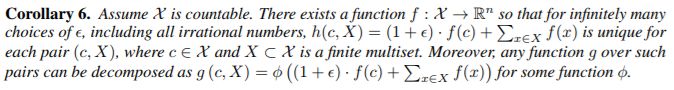
由于通用逼近定理（Hornik 等，1989; Hornik，1991），我們可以使用多層感知器（MLP）來(lái)推導(dǎo)和學(xué)習(xí)推論 6 中的 f 和 φ，在實(shí)際應(yīng)用中，我們用一個(gè) MLP 對(duì) f (k+1) ? φ (k) 進(jìn)行建模，因?yàn)?MLP 可以表示函數(shù)的組成。在第一個(gè)迭代中，如果輸入特征是一個(gè)熱編碼，那么在求和之前不需要 MLP，因?yàn)樗鼈兊那蠛褪菃紊涞摹Ｎ覀兛梢灾谱饕粋€(gè)可學(xué)習(xí)的參數(shù)或固定的標(biāo)量。然后，GIN 更新節(jié)點(diǎn)表征如下：

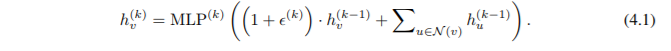
通常，可能存在許多其他強(qiáng)大的 GNNs。 雖然 GIN 很簡(jiǎn)單，但是它是最強(qiáng)大的 GNN 中的一個(gè)。

讀取不同部分的子樹結(jié)構(gòu)

圖級(jí)讀出（readout）的一個(gè)重要方面是，隨著迭代次數(shù)的增加，對(duì)應(yīng)于子樹結(jié)構(gòu)的節(jié)點(diǎn)表征變得更加精細(xì)和全局。足夠數(shù)量的迭代是實(shí)現(xiàn)良好區(qū)分力的關(guān)鍵。 然而，特征的早期迭代有時(shí)可能更好地泛化。為了考慮所有的結(jié)構(gòu)信息，GIN 從模型的所有深度 / 迭代使用信息。 我們通過(guò)類似于跳躍知識(shí)網(wǎng)絡(luò)（JK-Nets）（Xu 等人，2018）的架構(gòu)來(lái)實(shí)現(xiàn)這一點(diǎn)，其中在所有的迭代中我們使用連接后的圖的表征向量替換了 Eq.2.4：

根據(jù)定理 3 和推論 6，如果 GIN 使用對(duì)來(lái)自相同迭代的所有節(jié)點(diǎn)特征求和來(lái)取代 Eq.4.2 中的 READOUT（在求和之前我們不需要額外的 MLP，原因與方程 4.1 相同），它可以推廣 WL 測(cè)試和 WL 子樹核。

能力不強(qiáng)但仍然有趣的其他 GNNs

接下來(lái)我們研究不滿足定理 3 中條件的 GNN，包括GCN（Kipf＆Welling，2017）和GraphSAGE（Hamilton 等，2017a）。

我們對(duì) Eq. 4.1 中聚合器的兩個(gè)方面進(jìn)行消融研究：（1）使用 1 層的感知器代替 MLP；（2）利用平均或最大池而不是求和。

令人驚訝的是我們觀察到這些 GNN 變體被簡(jiǎn)單的圖所迷惑，并且沒(méi)有 WL 測(cè)試強(qiáng)大。 盡管如此，使用平均聚合器的模型像 GCN 在節(jié)點(diǎn)分類任務(wù)中還是表現(xiàn)良好。 為了更好地理解這一點(diǎn)，我們精確地描述了不同 GNN 變體能夠和不能夠捕獲圖的哪些內(nèi)容，并討論學(xué)習(xí)圖的含義。

1- 層的感知機(jī)并不充分

引理 5 中的函數(shù) f 有助于將不同的多重集合映射到唯一的嵌入。它可以通過(guò) MLP 通過(guò)通用逼近定理參數(shù)化（Hornik，1991）。盡管如此，許多現(xiàn)有的 GNN 使用 1- 層感知器 σ°W 代替（Duvenaud 等人，2015; Kipf＆Welling，2017; Zhang 等人，2018），線性映射后跟非線性激活函數(shù)，如 ReLU。 這種 1- 層映射是廣義線性模型的例子（Nelder＆Wedderburn，1972）。因此，我們對(duì)了解 1- 層感知器是否足以進(jìn)行圖學(xué)習(xí)非常感興趣。引理 7 表明確實(shí)存在網(wǎng)絡(luò)鄰域（多重集合），具有 1- 層感知器的模型永遠(yuǎn)無(wú)法區(qū)分。

引理 7. 定義如下：

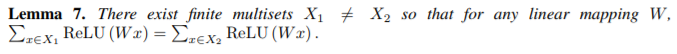
引理 7 證明的主要思想是 1 層感知器的行為很像線性映射，因此 GNN 層退化為簡(jiǎn)單地對(duì)鄰域特征求和。我們的證據(jù)建立在線性映射中缺少偏差項(xiàng)的事實(shí)上。利用偏差項(xiàng)和足夠大的輸出維數(shù)，1- 層感知器可能能夠區(qū)分不同的多重集。 盡管如此，與使用 MLP 的模型不同，1- 層感知器（即使具有偏置項(xiàng)）也不是多重集函數(shù)的通用逼近器。

因此，即使具有 1- 層感知器的 GNN 在某種程度上可以將不同的圖嵌入到不同的位置，這種嵌入也可能不能充分地捕獲結(jié)構(gòu)相似性，并且對(duì)于簡(jiǎn)單的分類器（例如，線性分類器）來(lái)說(shuō)可能難以擬合。 在第 7 節(jié)中，我們將憑經(jīng)驗(yàn)看到具有 1- 層感知器的 GNN，當(dāng)應(yīng)用于圖分類時(shí)，有時(shí)會(huì)嚴(yán)重欠擬合，并且在測(cè)試精度方面通常表現(xiàn)不及 MLP 的 GNN。

混淆平均值和最大池的結(jié)構(gòu)

如果我們將 h (X)=sum (f (x)) ，其中 x∈X，中的求和替換為 GCN 和 GraphSAGE 中的均值或最大池，會(huì)發(fā)生什么？平均和最大池聚合器仍然是定義良好的多重集函數(shù)，因?yàn)樗鼈兪侵脫Q不變的。但是，它們不是單射的。

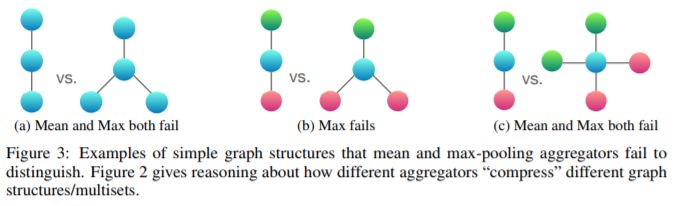
圖 2 根據(jù)三個(gè)聚合器的表示能力對(duì)其進(jìn)行排序，圖 3 說(shuō)明了平均池和最大池聚合器對(duì)結(jié)構(gòu)對(duì)無(wú)法區(qū)分。在這里，節(jié)點(diǎn)顏色表示不同的節(jié)點(diǎn)特征，我們假設(shè) GNN 在將它們與中心節(jié)點(diǎn)組合之前先聚合鄰居。

在圖 3a 中，每個(gè)節(jié)點(diǎn)具有相同的特征 a，并且 f (a) 在所有節(jié)點(diǎn)上是相同的（對(duì)于任何函數(shù) f）。當(dāng)執(zhí)行鄰域聚合時(shí)，f (a) 上的均值或最大值仍為 f (a)，并且通過(guò)歸納，我們總是在任何地方獲得相同的節(jié)點(diǎn)表示。因此，均值和最大池聚合器無(wú)法捕獲任何結(jié)構(gòu)信息。相反，求和聚合器可以區(qū)分結(jié)構(gòu)，因?yàn)?2?f (a) 和 3?f (a) 給出了不同的值。相同的參數(shù)可以應(yīng)用于任何未標(biāo)記的圖。如果節(jié)點(diǎn)度不是常量值，則可以用作節(jié)點(diǎn)輸入特征，原則上，均值可以覆蓋求，但最大池不能。

圖 3a 表明均值和最大值難以區(qū)分具有重復(fù)特征的節(jié)點(diǎn)的圖。假設(shè) h (color)（r 代表紅色，g 代表綠色）表示由 f 轉(zhuǎn)換后的節(jié)點(diǎn)特征。圖 3b 顯示藍(lán)色節(jié)點(diǎn)附近的最大值產(chǎn)生 max (h (g),h (r)) 和 max (h (g),h (r),h (r))，這兩個(gè)值折疊成相同的表示。因此，最大池?zé)o法區(qū)分它們。相比之下，求和聚合器仍然有效，因?yàn)?1/2*(h (g)+h (r)) 和 1/3*(h (g)+h (r)+h (r)) 通常是不等同的。同樣地，在圖 3c 中，平均值和最大值均為失敗 1/2*(h (g)+h (r)) 和 1/4*(h (g)+h (g)+h (r)+h (r))。

平均學(xué)習(xí)分布

為了描述平均聚合器可以區(qū)分多重集的類，考慮示例 X1 = (S, m) and X2 = (S, k?m)，其中 X1 和 X2 具有相同的一組不同元素的集合，但 X2 包含 X1 的每個(gè)元素的 k 個(gè)副本。任何平均聚合器都將 X1 和 X2 映射到相同的嵌入，因?yàn)樗恍枰獙?duì)單個(gè)元素的特征取平均值。因此，平均值可以捕獲多重集中元素的分布（或者比例），而不是精確的多重集。

推論 8.定義如下：

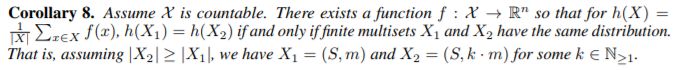
對(duì)于任務(wù)而言，如果圖中的統(tǒng)計(jì)和分布信息比精確的結(jié)構(gòu)更為重要，則平均聚合器可能表現(xiàn)良好。此外，當(dāng)節(jié)點(diǎn)特征多樣且很少重復(fù)時(shí)，平均聚合器與求和聚合器一樣強(qiáng)大。這就可以解釋為什么，盡管存在第 5.2 節(jié)中提到的一些限制，但帶有平均聚合器的 GNN 對(duì)于節(jié)點(diǎn)分類任務(wù)還是有效，例如對(duì)文章主題進(jìn)行分類和社區(qū)檢測(cè)，其中節(jié)點(diǎn)特征豐富，并且鄰域特征的分布為任務(wù)提供了一個(gè)強(qiáng)有力的信號(hào)。

具有不同元素的最大池學(xué)習(xí)集

圖 3 中的示例說(shuō)明最大池認(rèn)為具有相同的特征的多個(gè)節(jié)點(diǎn)僅為一個(gè)節(jié)點(diǎn)（即，將多重集合視為一個(gè)集合）。 最大池不捕獲確切的結(jié)構(gòu)和分布。 但是，它可能適用于某些識(shí)別任務(wù)，這些任務(wù)中識(shí)別元素或 “骨架” 更重要，而不是區(qū)分確切的結(jié)構(gòu)或分布。（ 齊等人.2017）憑經(jīng)驗(yàn)表明，最大池聚合器學(xué)習(xí)識(shí)別 3D 點(diǎn)云的骨架，并且它對(duì)噪聲和異常值具有魯棒性。 為了完整起見(jiàn)，下一個(gè)推論顯示最大池聚合器捕獲多重集的基礎(chǔ)集。

推論 9. 定義如下

實(shí)驗(yàn)設(shè)置

我們?cè)u(píng)估和比較 GIN 和不太強(qiáng)大的 GNN 變體的訓(xùn)練和測(cè)試性能。

數(shù)據(jù)集

我們使用 9 個(gè)圖分類基準(zhǔn)：4 個(gè)生物信息學(xué)數(shù)據(jù)集（MUTAG，PTC，NCI1，PROTEINS）和 5 個(gè)社交網(wǎng)絡(luò)數(shù)據(jù)集（COLLAB，IMDB-BINARY，IMDB-MULTI，REDDIT-BINARY 和 REDDIT-MULTI5K）（Yanardag＆Vishwanathan，2015）。

在生物信息圖中，節(jié)點(diǎn)具有分類輸入特征；在社交網(wǎng)絡(luò)中，它們沒(méi)有任何特征。 對(duì)于 REDDIT 數(shù)據(jù)集，我們將所有節(jié)點(diǎn)特征向量設(shè)置為相同（因此，這里的特征是無(wú)信息的）; 對(duì)于其他社交圖，我們使用節(jié)點(diǎn)度的獨(dú)熱編碼。

模型和配置

我們?cè)u(píng)估 GIN（方程 4.1 和 4.2）和不太強(qiáng)大的 GNN 變體。在 GIN 框架下，我們考慮兩種變體：1）通過(guò)梯度下降，學(xué)習(xí)方程式 4.1 中的 ε 的 GIN，我們稱之為 GIN-ε；（2）更簡(jiǎn)單（稍微不那么強(qiáng)大）的 GIN，其中 ε 在方程式中 4.1 固定為 0，我們稱之為 GIN-0。

正如我們將要看到的，GIN-0 顯示出強(qiáng)大的經(jīng)驗(yàn)性能：GIN-0 不僅與 GIN-ε 一樣擬合的訓(xùn)練數(shù)據(jù)好，它還表現(xiàn)出良好的泛化性，在測(cè)試精度方面略微但始終優(yōu)于 GIN-ε。對(duì)于能力較弱的 GNN 變體，我們考慮使用 mean 或 max-pooling 替換 GIN-0 聚合中的求和的架構(gòu)，或者用 1- 層感知器替換 MLP，即線性映射后面接 ReLU。在圖 4 和表 1 中，模型由它使用的聚合器 / 感知器命名。我們對(duì) GIN 和所有 GNN 變體應(yīng)用相同的圖級(jí) readout（公式 4.2 中的 READOUT），特別是生物信息學(xué)數(shù)據(jù)集的求和 readout 以及由于更好的測(cè)試性能而在社交數(shù)據(jù)集上的平均 readout。

以下（Yanardag＆Vishwanathan，2015; Niepert 等，2016），我們使用 LIB-SVM 進(jìn)行 10 倍交叉驗(yàn)證（Chang＆Lin，2011）。我們公布了通過(guò) cv 進(jìn)行的 10- 交叉驗(yàn)證 validate 集的準(zhǔn)確度的平均值和標(biāo)準(zhǔn)差。對(duì)于所有的配置，應(yīng)用 5 個(gè) GNN 層（包括輸入層），并且所有 MLP 具有 2 個(gè)層。BN 標(biāo)準(zhǔn)化（Ioffe＆Szegedy，2015）應(yīng)用于每個(gè)隱藏層。我們使用 Adam 優(yōu)化器（Kingma＆Ba，2015），初始學(xué)習(xí)率為 0.01，并且每 50 個(gè) epochs 將學(xué)習(xí)率衰減 0.5。我們針對(duì)每個(gè)數(shù)據(jù)集調(diào)優(yōu)的超參數(shù)是：（1）生物信息圖的 hidden units 的大小∈{16,32} 和社交圖的大小為 64; （2）批量大小（batch size）∈{32,128}; （3）在 dense 層后，dropout 率∈{0,0.5}（Srivastava 等，2014）; （4）epochs 的數(shù)量。

基準(zhǔn)線

我們將上面的 GNN 與一些性能最佳的圖分類基線進(jìn)行了比較：

（1）WL 子樹內(nèi)核（Shervashidze 等，2011），其中使用了 C-SVM（Chang&Lin，2011） 作為分類器。 我們調(diào)優(yōu)的超參數(shù)是 SVM 中的 C 和 WL 迭代的數(shù)量∈{1,2，...，6};

（2）性能最佳的深度學(xué)習(xí)架構(gòu)擴(kuò)散 - 卷積神經(jīng)網(wǎng)絡(luò)（DCNN）（Atwood＆Towsley，2016）、PATCHY-SAN（Niepert 等，2016）和 Deep Graph CNN（DGCNN）（Zhang et al.，2018）;

（3）Anonymous Walk Embeddings（AWL）（Ivanov＆Burnaev，2018）。

對(duì)于深度學(xué)習(xí)方法和 AWL，我們報(bào)告了原始論文中報(bào)告的準(zhǔn)確性。

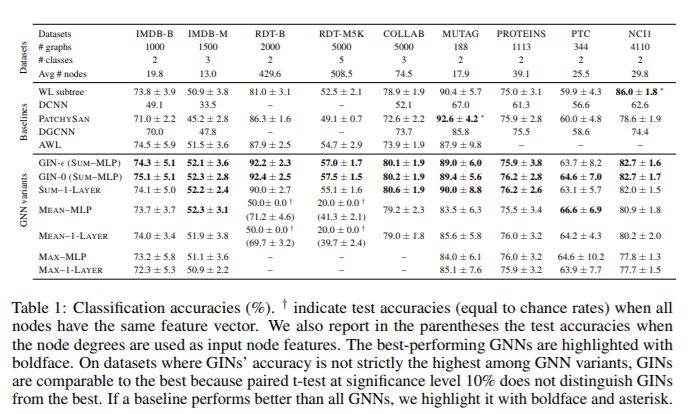
實(shí)驗(yàn)結(jié)果

訓(xùn)練集性能

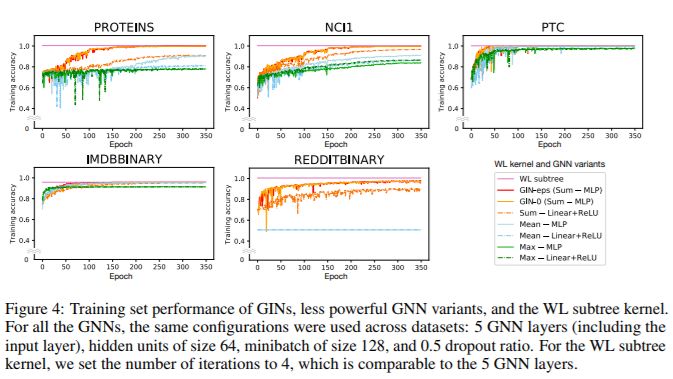
通過(guò)比較它們的訓(xùn)練精度，我們驗(yàn)證了 GNNs 的強(qiáng)大表征能力的理論分析。圖 4 顯示了具有相同超參數(shù)設(shè)置的 GIN 和不太強(qiáng)大的 GNN 變種的訓(xùn)練曲線。

首先，理論上最強(qiáng)大的 GNN，即 GIN-ε (Sum–MLP)，和 GIN-0 能夠完美擬合所有的訓(xùn)練數(shù)據(jù)。在我們的實(shí)驗(yàn)中，與在 GIN-0 中把 ε 固定為 0 相比，在擬合訓(xùn)練數(shù)據(jù)時(shí)，用 GIN-ε 顯式學(xué)習(xí) ε 沒(méi)有任何收益。相比之下，在許多數(shù)據(jù)集中，使用平均 / 最大池或 1- 層感知機(jī)的 GNN 變體嚴(yán)重欠擬合。特別是，訓(xùn)練精度模式與我們通過(guò)模型的表征能力進(jìn)行的排名一致：具有 MLP 的 GNN 變體比具有 1- 層感知器的 GNN 變體具有更高的訓(xùn)練精度，具有求和聚合器的 GNN 比具有平均和最大池聚合器的 GNN 更好的擬合訓(xùn)練集。

然而，在我們的數(shù)據(jù)集上，GNN 的訓(xùn)練精度從未超過(guò) WL 子樹內(nèi)核的精度，后者具有與 WL 測(cè)試相同的區(qū)分能力。例如，在 IMDBBINARY 上，沒(méi)有一個(gè)模型能夠完全擬合訓(xùn)練集，而且 GNN 最多能達(dá)到與 wl 內(nèi)核相同的訓(xùn)練精度。此模式與我們的結(jié)果一致，即 WL 測(cè)試為基于聚合的 GNN 的表示能力提供了一個(gè)上限。我們的理論結(jié)果集中在表征能力上，還沒(méi)有考慮到優(yōu)化（例如局部極小）。盡管如此，實(shí)驗(yàn)結(jié)果與我們的理論非常吻合。

測(cè)試集性能

接下來(lái)，我們比較測(cè)試集精度。雖然我們的理論結(jié)果并不能直接說(shuō)明 GNN 的泛化能力，但有理由期待具有較強(qiáng)表達(dá)力的 GNN 能夠準(zhǔn)確地捕獲感興趣的圖結(jié)構(gòu)，因此泛化能力非常好。表 1 比較了 GINs (SUM-MLP)、其他 GNN 變種以及最佳基準(zhǔn)線的測(cè)試精度。

結(jié)論

在本文中，我們建立了 GNN 表達(dá)能力推理的理論基礎(chǔ)，并對(duì)流行的 GNN 變體的表達(dá)能力進(jìn)行了嚴(yán)格的論證。在此過(guò)程中，我們還在鄰域聚合框架下設(shè)計(jì)了一個(gè)可以證明是最強(qiáng)大的 GNN。未來(lái)工作的一個(gè)有趣方向是超越鄰域聚合（或消息傳遞）框架，以追求更強(qiáng)大的圖學(xué)習(xí)架構(gòu)。理解和改進(jìn) GNN 的泛化性質(zhì)也是很有意思的。