摘要：計算神經科學是一門超級跨學科的新興學科，幾乎綜合信息科學，物理學， 數學，生物學，認知心理學等眾多領域的最新成果。關注的是神經系統的可塑性與記憶，抑制神經元與興奮神經元的平衡。

0 背景

計算神經科學是一門超級跨學科的新興學科，幾乎綜合信息科學，物理學， 數學，生物學，認知心理學等眾多領域的最新成果。關注的是神經系統的可塑性與記憶，抑制神經元與興奮神經元的平衡。計算神經科學在做的事情是先主動設計這個一個系統，看看如何做到需要的功能（自上而下），然后拿著這個東西回到生物的世界里去比較（由下而上）。人工智能和計算神經科學具有某種內在的同質性， 唯一的區別可能是人工智能可以不必拘泥生物的限制，或者也是為什么他最終或許會比生物網絡表現更好。

今年的計算與系統神經科學大會 -Cosyne在葡萄牙結束。 這個會議和nips都是神經網絡與計算方面的最重要盛會， 而方向上一個更偏深度學習， 一個更偏和生物有關的計算。而近兩年的趨勢是， 兩個會議的交叉主題越來越多。 對于會議涵蓋的幾個方面， 做一個小的總結，也算涵蓋了計算神經科學的主要方面。

1： 前饋網絡：如何讓深度學習工作更像人腦

在這個session， Yann Lecun 作為邀請演講人， 總結了CNN受生物神經網絡啟發的歷史， 并提出他最近的核心方向 -learning predictive model of world（學習建立預測性的模型）。 指出深度學習的未來在于以建立預測性模型為核心的半監督學習， 這樣可以彌補普通的監督學習或model free reinforcement learning（無模型強化學習）的巨大缺陷-缺乏穩定的先驗模型。 比如你要做一個視頻有關的處理， 讓他看完youtube上的視頻并不停的預測視頻下一幀的狀態， 這樣預訓練后再去進行任何任務都會更方便。 yann認為這是dl的未來方向。

一個目前突出的成就是大量預訓練產生的NLP模型Bert在各大任務上都破了記錄。 關于如何進行半監督學習， auto-encoder和對抗學習都是方向。 在此處無監督，監督， 和強化學習的界限已經接近。 強化學習不再只是蛋糕上的櫻桃， 無監督學習也不再是難以操作的暗物質。 預測性學習用的是監督學習的方法， 干的是無監督學習的事情， 而最后被用于強化學習。 不難看出， 這個方法論和計算神經科學領域的predictive coding間的聯系， 和好奇心的聯系。 整個工作都符合Karl Friston 關于自由能最小的理論框架。

有關前饋網絡和計算神經科學的交叉， 另外幾個speaker 著重在于研究生物系統如何實現類似反向傳播算法的過程。 反饋的神經信號和local的Hebbian rule等的結合， 可以實現類似于反向傳播的修正，也就是說大家在尋找反向傳播的生物基礎，而且還非常有希望。

當然比較CNN不同層次的representation 和生物視神經的表示已經是老課題， 目前imagenent上預訓練的網絡經常被用來和生物神經網絡的活動比較， 逐步被作為一種衡量生物神經網絡表達復雜度的標尺， 也是一個有意思的方法。

2，多巴胺（Dopamine）在學習回路中的作用（Ilan Witten， Princeton）

多巴胺神經元和回路是計算神經科學和強化學習的熱點問題， 它與我們的一切行為有關， 影響我們的喜樂哀愁。 dopamine的經典理論被認為傳遞對未來獎勵的預期信息和真實獎勵的差距， 這恰好對應強化學習理論的TD誤差。 后來人們發現這個想法太簡單了。 一些新的結果指出dopamine神經元作為一個數量巨大的群體，編碼的信息不僅包括獎勵信號， 還有和獎勵有關的的信號特征，比如顏色，物體的運動方向。生物系統為什么這樣選擇自己的強化學習算法， 非常值得探討。

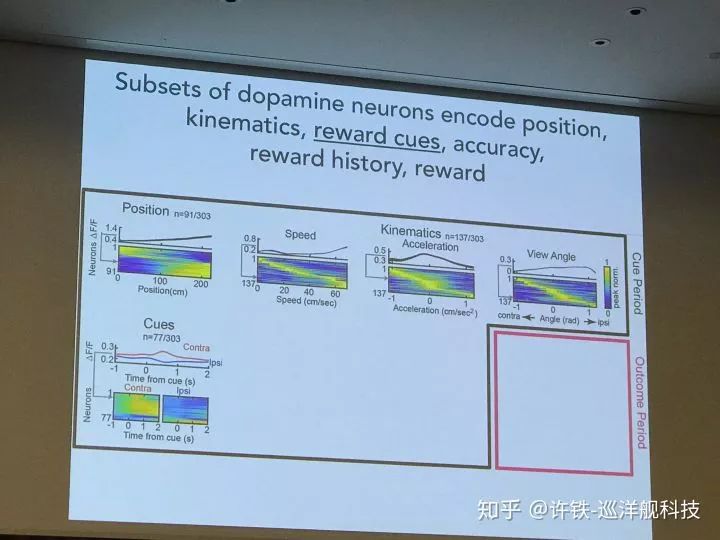
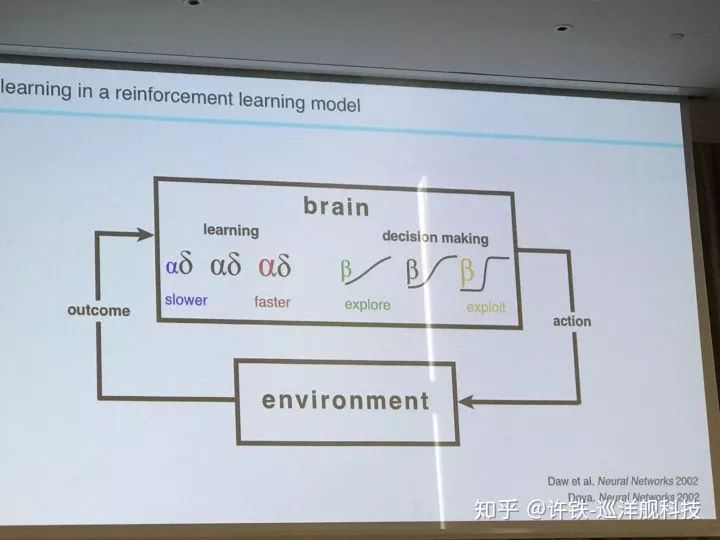
另一些工作圍繞dopamine和強化學習的研究通過實驗驗證dopamine的數學理論， 模型結合實驗的方法可以很好的test這方面的idea。 人們一直在爭論dopamine對應value function本身還是TD誤差， 你能不能設計一個研究的方法很好的區分了前者和后者？ 事實上真實情況永遠比理論模型復雜的多。

3.神經編碼的本質： 高維vs低維（Kenneth Harris， UCL）

大家都知道人腦有1000億個神經元， 近似于我們說的無窮多，為什么？為什么要這么多？

神經編碼的本質屬性是維度， 大部分時候， 當我們對世界的理解抽離到最后， 就只剩下維度。 首先神經編碼必須是高維的， 這對應我們的大千世界信息是豐富的。 同時我們又不希望神經編碼的維度太高，我們們希望在能夠表達現實世界的豐富信息的時候， 這個表征流行的維度越低越好， 反過來說，就是我們希望在某種限制條件下盡可能充分的表達真實世界的信息。 其背后的合理性是什么？

這組實驗讓小鼠不停的觀測從自然環境中隨機抽取的圖像樣本（nature image）， 然后我們記錄視皮層的神經活動， 并通過PCA等降維手段來觀測神經表征里的維度。 首先， 我們最終得到的結果是我們的生物神經網絡確實具有無窮多（和圖像的總數一樣多）的維度（所以需要無窮多神經元表達）, 這是由于自然環境中的物體太豐富了，自然信息的維度可以是接近正無窮， 這也是為什么我們的腦內需要這么多的神經細胞。

然后， 我們發現并非每個維度都是均衡的， 每個PC維度所刻畫的信息量均勻的下降， 而且這個下降呈現的衰減符合一個冪律分布。 而這個冪律的數值非常關大。 我們知道這個數值越小， 衰減就越慢，冪律就越接近肥尾， 這背后對應的是什么呢？ 如果我們用流型的思維看， 這個指數大小正對應流行曲面的形狀（你可以想象一下極限情況， 如果我們只有兩個PC，后面的數值均是0，我們的流型是一個平面） 。 越小的指數， 代表高維的成分越顯著，流型維度大到一定程度， 就會出現分型結構（連續但不可導）。 一個高維的分型結構意味著，每個樣例可能都占據著一個高峰， 而稍微一離開， 就是波谷。

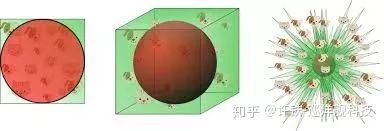
從低維流型到高維分型

這在機器學習里，恰恰意味著泛化能力很差， 如果你稍微移動一下這個曲面， 分類就可能變化。 如果指數比較大呢？ 指數比較大， 意味著高維成分衰減很快， 這個時候， 我們會得到更為平滑的流行曲面，從而得到更好的泛化能力。那么指數可不可以盡量高呢？ 答案是不行， 因為那樣導致的表征維度過低， 剛剛已經說了很多遍，那樣我們就失去了對豐富世界的表達能力（維度越高越好做分類，可以容納更多互相正交的分類， 模型容量高）。

總結一下這個冪律的指數值有兩個關鍵點， 當指數比較小的時候流形都是剛剛講的分型結構， 第一個關鍵點是從分型到平滑， 而第二個關鍵點是神經全息成像， 當衰減速度快到一定程度（低維到一定程度）， 我們就會得到類似全息成像的現象，此時神經信息處處是冗余， 你隨便找一組神經元都可以得到整個外部世界的信息。

自然界用高維冗余的非線性系統表達低維的表征，來對現實世界降維。 這是神經科學和深度學習恒久不變的主題。 一般情況下高維會增加分類的效率和模型的容量(正交性)， 而低維則有利于泛化（平滑性， 把相關類別的編碼放到一起）。 而在當下的深度學習里， 我們恰恰缺乏這種能力， 用同樣的指數實驗測量CNN的信息壓縮特性， 我們發現， 它的指數衰減明顯的慢于小鼠，也就是依然保留了更多高維成分， 這使得它對高維信息（往往在空間上意味著高頻）極為敏感。 當你在已經識別很好的圖像加一點噪聲（高頻信息）它就認錯了。

這個講話解釋了很多困擾我的謎團， 比如為什么需要那么多神經元， 深度學習的泛化問題等等， 同時把學習算法和冪律巧妙的聯系在了一起。

自然圖像與神經活動中的冪律

4， 尋找RNN的動力學維度

（Eric Shea-Brown， Univesity of Washington）

另一個研究指出用RNN解決任務時候自身動力學維度與任務維度的匹配關系。 如何預測RNN所表征的系統維度？ 首先維度取決于背后的動力學， 然后網絡的動力學取決于結構， 我們可以用一套啟發于物理學的方法來從結構推出動力學維度。 這個方法通過定位神經網絡里的motif來預測其維度， 可以說和費曼的場論異曲同工。

然后這個維度有什么意義？ 我們說這個維度與我們要執行任務本身的復雜度高度相關。如果換一個在平面上的簡單分類， 我們不需要實用自身動力學維度很高的系統做， 而如果這個分類就是高維的， 那么具有高維動力學的系統往往優于低維的。 這揭示了網絡動力學與真實世界動力學的內在聯系。而事實上， 一般在混沌狀態的網絡動力學維度更高， 這無形中揭示了，混沌沒有看上去混亂，它可能恰恰是我們強大認知能力的基礎。

5， 生物導航Navigation

（Edward Moser， Kavli institute, grid cell諾貝爾獎得主）

導航與空間運動相關的問題一直是計算神經科學的熱點主題。 grid cell實現所謂的物體位置編碼，可以把空間里的核心物體位置編碼成一組向量。 這種能力是如何一點點隨學習和發育產生的? 這是一個非常大的主題，也是無數計算神經科學家的目標。

Navigation的一個核心主題是cognitive map 的理論。 它說的是在大腦中存在一個空間表示的神經載體。 你我都存在在這個認知空間里， 它獨立于你我而存在。 根據Okeefe的理論， 這個空間是hippocampus的grid cells 和place cell 作為基礎提供的。 grid cell類似于一個巨大的坐標系統， 而place cell 可以在每個不同的空間里重新編碼（remapping）。 這個十分有魅力的理論至今其實很多問題依然是懸案。

在這次的會議上， grid cell 理論的創始人Moser給了key speech， 他主要描述了這種空間的神經編碼應該以對空間的物體進行向量編碼為基礎， 每個物體對應一個向量編碼。 同時， 他講解了提供這種空間結構的基礎網絡是如何從發育階段一點點形成的。 從發育階段理解一個復雜問題通常可以把這個問題簡化。

圍繞這一主題的其它講話里有幾個來自以色列的研究特色鮮明。維茲曼研究所的 Alon Rubin 揭示出我們所認為的認知地圖即使對應同一個環境也不僅有一個，在同一個房間運動的小鼠可以解碼若干地圖， 這一點讓我們不僅思考這些地圖到底是干什么的， 顯然它們與不只對應我們所認識的絕對空間， 因為絕對空間只有一個。

另一個來自以色列的Gily嗎Ginosar 則展示了如何尋找蝙蝠頭腦里的grid cell， 并揭示出它符合一個三維空間的密堆積周期結構 。 因為蝙蝠的生活空間是三維的， 所以顯然它的空間表征也要是這個維度。 這點讓我們不禁想象， 如果存在4維和5維的空間，這個表示是什么樣的？ 到底是我們的認知確定了我們的世界， 還是我們的世界決定了我們的認知？

另外一個核心問題是我們頭腦里的認知地圖是egocentric(自我中心) 還是allocentric（外部環境中心），所謂以自我為中心（以上下左右表達整個世界，自我就是坐標原點）， 還是以一個外界的坐標系（如不同的地標）為中心。 經典的認知地圖模型是allocentric的外部坐標表示， 然而事實上很多研究指出， 自我為中心可以找到很多實驗證據 。因此兩個派別進行了激烈的辯論。

當然也有些會議上的報告討論了place cell的真實性“它們可能僅僅是一些依照時間序列依次發放的神經集團” 來自MIT的Buffalo指出。

最后， 這個方向的討論還包含了這種能力是否能夠提供空間之外的推理能力？來自馬普所的教授進行了很好的開拓性發言，它認為空間的grid cell 可以作為我們的其它推理能力的一種基礎形式。

蝙蝠的三維grid cell

6對不確定性的神經編碼（Maneesh Sahani, Gatesby Unit UCL）

神經系統如何通過大量的神經元編碼周邊信號的不確定性是一個很重要的課題，一個有意思的主題是集群編碼（population coding）。這方面的研究和機器學習里variational auto-encoder （VAE）密切相關。 因為你要決策， 不僅要依靠確定性的信息， 還要靠不確定的信息， 比如distribution。 神經網絡被認為具有這種編碼不確定性的能力。 同時這也是機器學習的核心主題， 貝葉斯學習基礎的神經網絡-深度貝葉斯學習正在占據越來越大的研究空間。

7貝葉斯學習(Weiji Ma, New york University)

貝葉斯學習和上面的不確定性密切相關。 貝葉斯相關的模型可以迅速的建立同時包含數據和假設的模型。貝葉斯概率是非常基礎的統計知識， 有的人只把它當成統計， 而它在神經科學的巨大潛力在于， 它可以非常好的解釋行為， 以及大量之前模棱兩可的現象。 把實驗數據和理論做一個極好的結合。 因為通過貝葉斯方法， 你可以把現有的實驗數據迅速的通過似然性轉化為一個預測性模型，驗證你的假設。

貝葉斯模型有別其它更基礎的模型，可以直接在行為上建模。你只要有先驗， 有似然性， 就可以建立一個貝葉斯模型。比如你有兩個截然不同的假設解釋一種心理現象， 貝葉斯方法讓你直接把先驗和似然性（可以通過數據檢測或者直接推理得到）組合在一起解決一個問題。同時， 貝葉斯方法和自編碼器有很多靈活的結合， 不少新的工作圍繞如何在高斯假設之外實現變分自編碼器。

8 強化學習

強化學習相關的主題（如果包含多巴胺）幾乎占據了會議的半壁江山， 這些理論可以揭示動物的行為和決策后面的大量算法基礎。 神經科學方面， 大家圍繞stratum, amygdala, basal ganglia是如何配合實現這一算法展開了大量研究。 算法方面， 一些研究把小鼠海馬在空間導航學習中的預演“（preplay）和"回放“（replay）進行了對比。 預演很像有模型學習中的計劃和模擬部分， 而回放可以對應到TD lambda算法的值函數回傳， 這些算法， 都可以很好的對應到現代的深度強化學習里， 但并不是每一個AI里的強化學習算法都有很好的神經對應， 比如策略梯度。或許未來我們會發現兩者是一致， 或許不一致的部分正好可以指導我們改進AI。

最后， 一個有趣的研究（David Reddish）把強化學習和神經經濟學（neural economics）聯系起來， 讓小鼠在不同的選擇中權衡， 我們可以很輕易的控制每個獎賞的屬性（如時間， 獲取難度）， 看它怎么選擇。 有趣的是， 從小鼠中得到的現象居然可以直接和人類進行對比。

這讓我想到， 目前的大量心理學理論，甚至經濟學理論，可以通過強化學習， 與計算神經科學和AI聯系起來。

9， data inference & latent dynamics

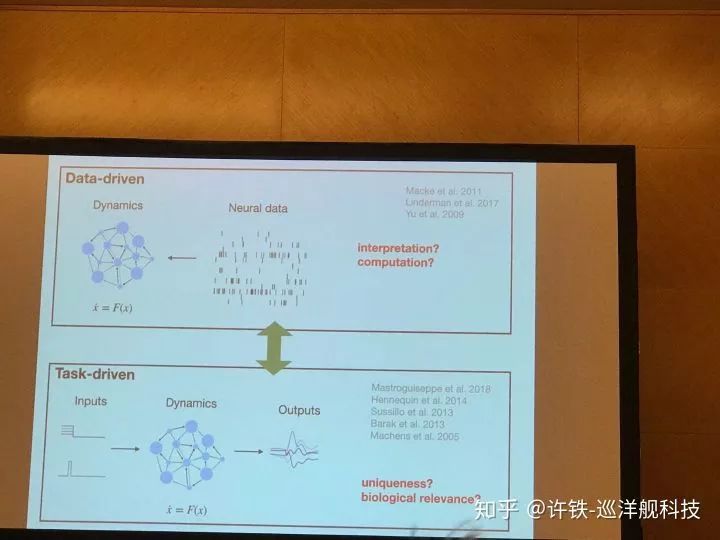
模型分成兩種， 一種叫做機理模型， 一種叫做數據模型。 所謂機理模型的核心是用第一型原理推出現象， 理解現象，比如神經細胞放電的Hodykin-Hukly模型，平衡神經網絡模型， 這些往往是傳統的計算神經科學模型。 而數據現象模型， 是力圖用最少的參數解決復雜的現象， 似乎理解了現象，然而實際只是擬合而已，但是這樣的模型有時候具有泛化能力， 它就是好的預測模型，幾乎所有的機器學習模型都可以進入這一類。

然而對于想理解大腦的人第二類模型是不靠譜的， 因為你又不是做股票 ， 你是想理解現象。而你確實希望讓第一種模型具有第二個的能力， 因為如果一個機理模型可以預測現象或數據， 你就更加確定它是合理的，甚至可以給出更靠譜的預測。 而現在，有一些方法可以把兩個模型合成成一種。其中的一大類方法基于貝葉斯推理， 因為貝葉斯可以把一個”生成模型“通過貝葉斯公式，和觀測數據結合起來， 得到一個模型參數的后驗概率， 事實上相當于你用數據而不是其它的擬合了你的機理模型。 然后我們可以把這個機理模型帶去預測新的現象 ，驗證它靠不靠譜。

而貝葉斯方法經常面臨的問題是先驗不好給出， 似然性不好求解。 一個更加fancy的方法是直接上機器學習里的神經網絡來做參數估計。 首先我們用我們”不靠譜“的機理模型通過模擬， 得到大量的結果。 每個模型參數，都得到一大類模擬結果。 這些模擬結果和參數， 就稱為了神經網絡的輸入和labels， 不過可能和你想的反過來， 模擬的結果是輸入， 而參數是輸出， 這個神經網絡所做的正是貝葉斯里的推測后驗概率，只不過先驗和似然性被包含在了模型里。由此訓練好的模型， 我要輸入給它最終測量到的真實數據， 它就會得到一組最后我想要的模型參數了。你也可以理解為它很像一個GAN的結構，機理模型在這里扮演了生成器的角色， 而神經網絡是一個判別器。 最終生成器生成的數據要和真實數據完全一致， 一個擬合就完成了。 由此你就得到了最具有預測力的機理模型。

另一些討論圍繞RNN，本次會議提到了一個GOLD模型 (Daniel O'shea Stanford)。用RNN可以學習執行一個任務，比如決策，但是以往我們不知道RNN的神經元活動和真實的關系。 現在， 執行任務的同時我們用類似剛剛的方法讓它擬合真實的實驗數據（神經元活動）， 由此我們認為，得到的RNN就是我們腦網絡的縮影，可以分析出大腦信息流動的基本原理。這類工作應該對構建大規模腦網絡非常有幫助。

Gold 模型實際用到的結構類似一個自編碼器， 一個編碼RNN把和任務有關的信息， 初始條件都壓縮成神經編碼， 而另一個解碼RNN， 則在所有這些信息基礎上做出最后的決策，并擬合真實數據。這一類數據反推得來的模型， 可以幫助我們尋找數據背后的神經活動本質，這一類認為又稱為Inference of latent dynamics.

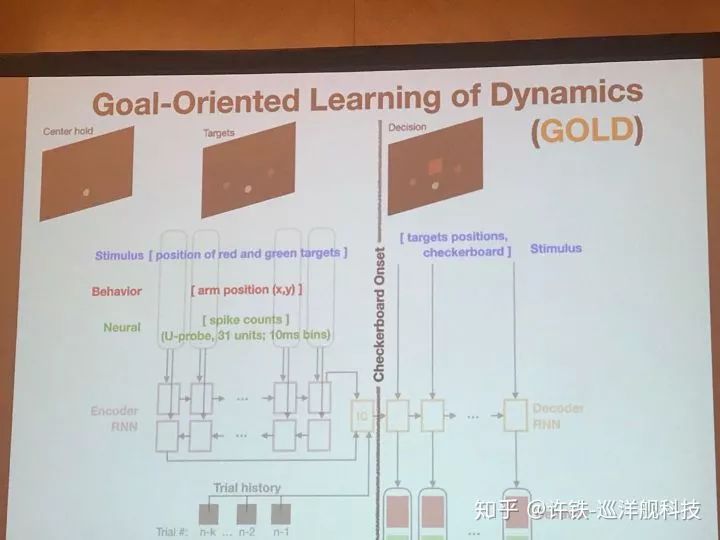
GOLD模型

10， 尋找真實神經網絡模型的神經連接

一些好的計算模型， 可以幫助我們找到兩個真實腦網絡模塊之間的連接， 讓我們知道它們是怎么被連在一起的。 這也是計算和實驗非常緊密在聯系在一起的一塊。 比如這次的會議一個talk講了初級視皮層V1區和V2區之間的功能連接可以如何通過數據推理出來。

總結：

這次會議展示了計算神經科學的巨大魅力和潛力，以及研究的挑戰。我們看到，火爆發展的機器學習的思想和方法， 已經滲入了計算神經科學的所有角度， 而對計算神經科學的理解， 也在幫助我們制定發展通用人工智能的潛在方法。 當然， 計算神經科學的作用遠不止這些， 它和所有的心理學，認知科學， 生物神經科學的關系猶如理論物理和物理的關系一樣緊密。 我經常驚嘆某個計算理論可以如何讓我們聯想到一些心理現象， 這個學科的發展與神經醫學的聯系也是不言而喻的。

然而進入這個學科的難度還是很大的， 真正要在這個領域做好研究， 需要精通數學里的高等代數和微積分， 機器學習和深度學習的所有理論， 物理里的非線性動力學和一部分統計物理知識， 要求不可謂不高。

最重要的，還要有極好的思辨能力。 因為這個學科不同于機器學習的是， 你不是光得到一個benchmark分數很高的模型預測性能就可以了， 而是要真正理解一個機理的， 本質性的東西。 你的模型永遠來源于真實， 又遠遠抽象于真實，如何知道你的東西不是一個toy model， 而是包含了這種本質的東西？ 這種思辨力可能才是這個學科最有門檻的東西， 也是最有魅力之處吧。