簡介
放大器的仿真模型通常是利用電阻、電容、晶體管、二極管、獨立和非獨立的信號源以及其它模擬元件來實現的。一種替代方法是使用放大器行為的二階近似(拉普拉斯轉換),這可加快仿真速度并將仿真代碼減少到三行。
然而,對于高帶寬放大器,采用s域傳遞函數的時域仿真可能非常慢,因為仿真器必須首先計算逆變換,然后利用輸入信號對其進行卷積。帶寬越高,則確定時域函數所需的采樣頻率也越高,這將導致卷積計算更加困難,進而減慢時域仿真速度。
本文進一步完善了上述方法,將二階近似合成為模擬濾波器,而不是 s域傳遞函數,從而大大提高時域仿真速度,特別是對于高帶寬放大器。
二階傳遞函數
放大器仿真模型的二階傳遞函數可以利用Sallen-Key濾波器拓撲實現,它需要兩個電阻、兩個電容和一個壓控電流源;或者利用多反饋(MFB)濾波器拓撲實現,它需要三個電阻、兩個電容和一個壓控電流源。這兩種拓撲給出的結果應相同,但Sallen-Key拓撲更易于設計,而MFB拓撲則具有更好的高頻響應性能,可能更適合可編程增益放大器,因為它更容易切換到不同的電阻值。
首先,利用二階近似的標準形式為放大器的頻率和瞬態響應建模:
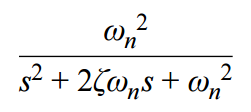
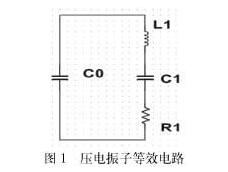
圖1顯示了如何轉換到Sallen-Key和多反饋拓撲。
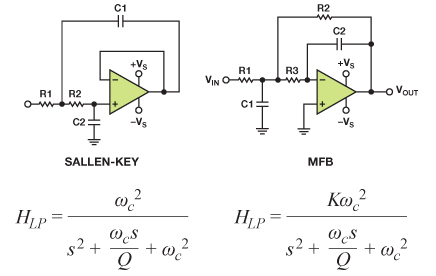
放大器的自然無阻尼頻率ωn等于濾波器的轉折頻率 ωc,放大器的阻尼比ζ 則等于 ?乘以濾波器品質因素Q 的倒數。對于雙極點濾波器, Q 表示極點到jω軸的徑向距離;Q 值越大,則說明極點離 jω軸越近。對于放大器,阻尼比越大,則峰化越低。這些關系為 s域 (s = jω) 傳遞函數與模擬濾波器電路提供了有用的等效轉換途徑。
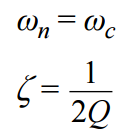
設計示例:5倍增益放大器
該設計主要包括三步:首先,測量放大器的過沖(Mp) 和建立時間 (ts)。其次,利用這些測量結果計算放大器傳遞函數的二階近似。最后,將該傳遞函數轉換為模擬濾波器拓撲以產生放大器的SPICE模型。
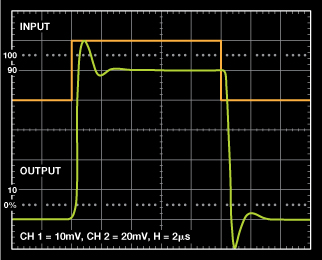
例如,利用Sallen-Key和MFB兩種拓撲仿真一款5倍增益放大器。從圖2可知,過沖(Mp) 約為22%,2%建立時間則約為2.18 μs。阻尼比ζ計算如下:
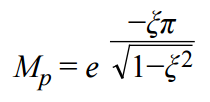
重排各項以求解ζ:
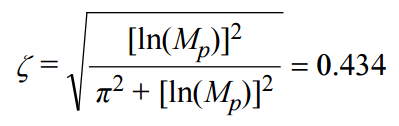
接下來,利用建立時間計算自然無阻尼頻率(單位為弧度/秒)。
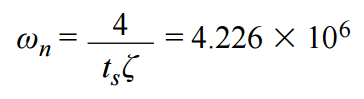
對于階躍輸入,傳遞函數分母中的 s2 和 s 項(弧度/秒)通過下式計算:
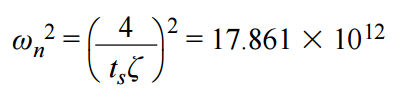
和
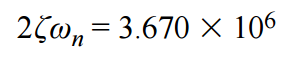
單位增益傳遞函數即變為:
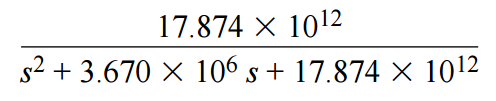
將階躍函數乘以5便得到5倍增益放大器的最終傳遞函數:
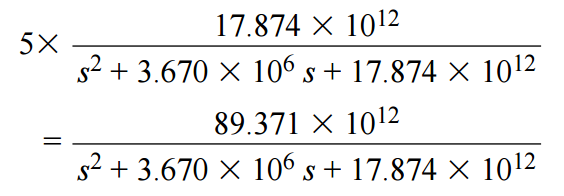
下面的網絡列表模擬5倍增益放大器傳遞函數的拉普拉斯變換。轉換為濾波器拓撲之前,最好運行仿真以驗證拉普拉斯變換,并根據需要延長或縮短建立時間以調整帶寬。
***GAIN_OF_5 TRANSFER FUNCTION***
.SUBCKT SECOND_ORDER +IN –IN OUT
E1 OUT 0 LAPLACE {V(+IN) – V(–IN)} = {89.371E12 / (S^2 + 3.670E6*S + 17.874E12)}
.END
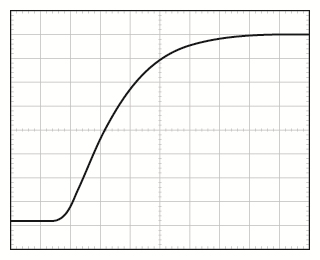
圖3所示為時域的仿真結果。圖4所示為頻域的仿真結果。
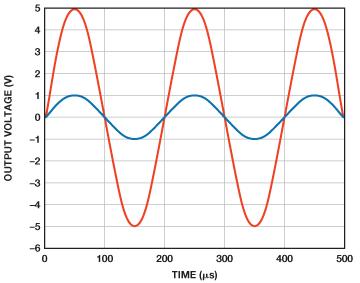
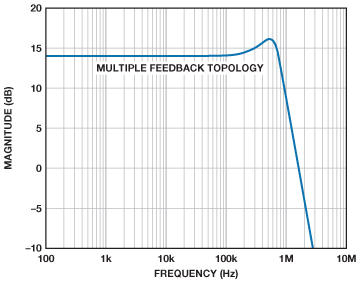
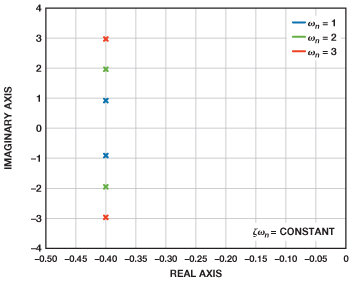
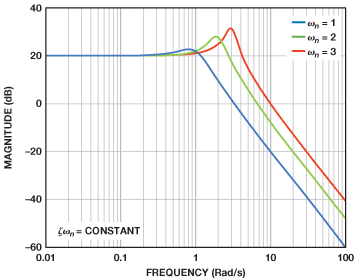
脈沖響應的峰化使得我們可以輕松保持恒定的阻尼比,同時可改變建立時間以調整帶寬。這將改變復數共軛極點對相對于實軸的角度,改變量等于阻尼比的反余弦值,如圖5所示。縮短建立時間會增加帶寬,延長建立時間則會減少帶寬。只要阻尼比保持不變且僅調整建立時間,則峰化和增益不受影響,如圖6所示。
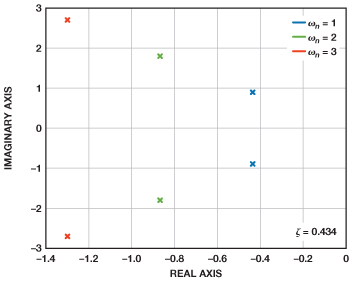
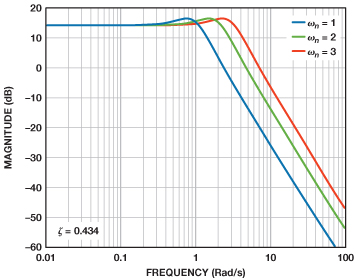
一旦傳遞函數與實際放大器的特性一致,就可以將其轉換為濾波器拓撲。本例將使用Sallen-Key和MFB兩種拓撲。
首先,利用單位增益Sallen-Key拓撲的正則形式將傳遞函數轉換為電阻和電容值。
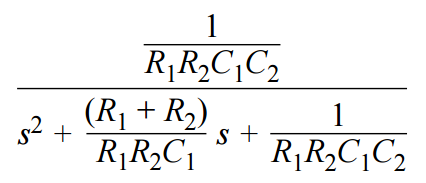
根據 s項可以計算 C1:
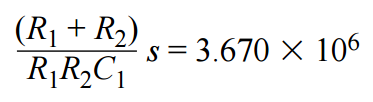
選擇易于獲得的電阻值,例如R1和R2均為10 kΩ,然后計算C1。
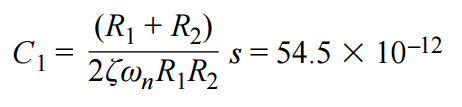
利用轉折頻率的關系式求解C2。
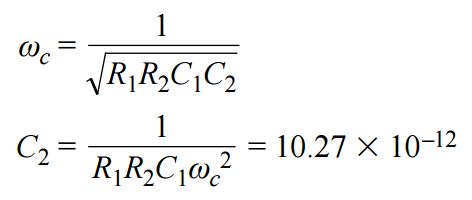
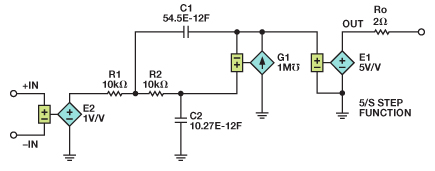
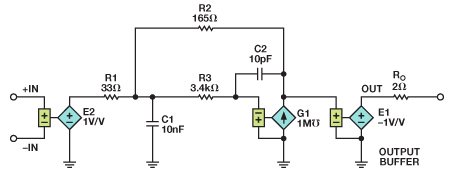
相應的網絡列表如下文所示,Sallen-Key電路則如圖7所示。E1乘以階躍函數以獲得5倍增益。Ro提供2 Ω輸出阻抗。 G1 是增益為 120 dB的VCCS。 E2為差分輸入模塊。頻率與增益的仿真與采用拉普拉斯變換的仿真完全相同。
.SUBCKT SALLEN_KEY +IN –IN OUT
R1 1 4 10E3
R2 5 1 10E3
C2 5 0 10.27E–12
C1 2 1 54.5E–12
G1 0 2 5 2 1E6
E2 4 0 +IN –IN 1
E1 3 0 2 0 5
RO OUT 3 2
.END
接下來,利用MFB拓撲的標準形式將傳遞函數轉換為電阻和電容值。
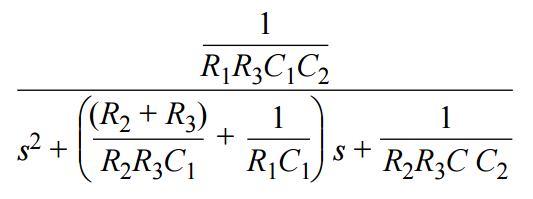
從計算R2開始轉換。為此,可以將傳遞函數改寫為以下更為通用的形式:
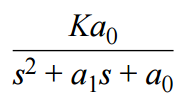
設置 C1 = 10 nF,然后選擇C2 ,使得根號下的量為正數。為方便起見,選擇C2 為 10 pF。代入已知值 C2 = 10 pF、 a1 = 3.67E6、K = 5、 a0 = 17.86E12 ,計算R2值:
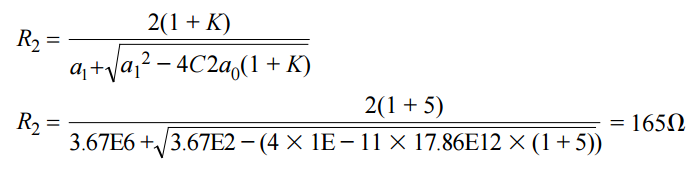
R1 的值很容易計算,等于 R2/K = R2/5 = 33。根據標準多項式系數可求解 R3。代入a0、R2和 C2 的已知值可得:
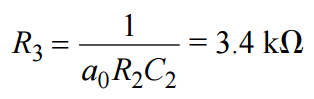
最后,驗證元件比是否正確,即代入a0、R2、 R3、增益K和 C2 (從s 項求得)的已知值時,C1 應等于10 nF。
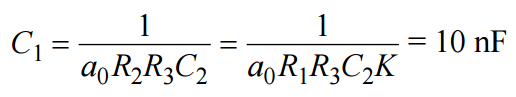
得出元件值后,再代入方程式中,驗證多項式系數在數學上是否正確。利用電子表格計算器就能輕松完成這項工作。所示的元件值是可以用于最終SPICE模型的實際值。實際應用中,應確保最小電容值不低于10 pF。
5倍增益放大器的網絡列表如下文所示,模型則如圖8所示。G1是開環增益為120 dB的VCCS(壓控電流源)。注意,如果使用電阻、電容、二極管和非獨立源,所需的元件數將多得多
.SUBCKT MFB +IN –IN OUT
***VCCS – 120 dB OPEN_LOOP_GAIN***
G1 0 7 0 6 1E6
R1 4 3 330
R3 6 4 34K
C2 7 6 1P
C1 0 4 1N
R2 7 4 1.65K
E2 3 0 +IN –IN 1
E1 9 0 7 0 –1
***OUTPUT_IMPEDANCE RO = 2 Ω***
RO OUT 9 2
.END
設計示例:10倍增益放大器
在第二個示例中,考慮一個無過沖10倍增益放大器的脈沖響應,如圖9所示。建立時間約為7 μs。由于無過沖,脈沖響應可以近似為具有臨界阻尼, ζ ≈ 0.935 (Mp = 0.025%)。
在無過沖的情況下,很容易保持恒定的建立時間,并調整阻尼比以模擬正確的帶寬和峰化。圖10顯示了極點如何隨阻尼比而變化,與此同時建立時間保持不變。圖11顯示了頻率響應的變化情況。
***AD8208 PREAMPLIFIER_TRANSFER_FUNCTION (GAIN = 20 dB)***
.SUBCKT PREAMPLIFIER_GAIN_10 +IN –IN OUT
E1 OUT 0 LAPLACE {V(+IN)–V(–IN)} = {3.734E12 / (S^2 + 1.143E6*S + 373.379E9)}
.END
為求得單位增益拓撲的電阻和電容值,請像前面一樣選擇R1 = R2 = 10 kΩ 。利用與5倍增益放大器示例相同的方法計算電容值:
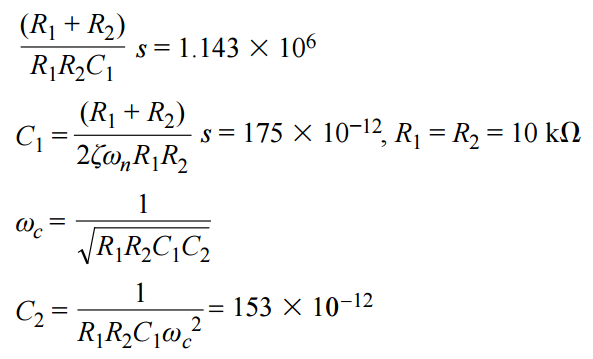
網絡列表如下文所示,Sallen-Key仿真電路模型則如圖12所示。E2是一個10倍增益模塊,與一個2 Ω輸出阻抗一起置于輸出級。E2將單位增益傳遞函數放大10倍。拉普拉斯變換和Sallen-Key網絡列表產生的仿真相同,如圖13所示。
***AD8208 PREAMPLIFIER_TRANSFER_FUNCTION (GAIN = 20 dB)***
.SUBCKT AMPLIFIER_GAIN_10_SALLEN_KEY +IN –IN OUT
R1 1 4 10E3
R2 5 1 10E3
C2 5 0 153E–12
C1 2 1 175E–12
G1 0 2 5 2 1E6
E2 4 0 +IN –IN 10
E1 3 0 2 0 1
RO OUT 3 2
.END
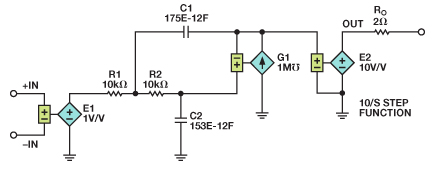
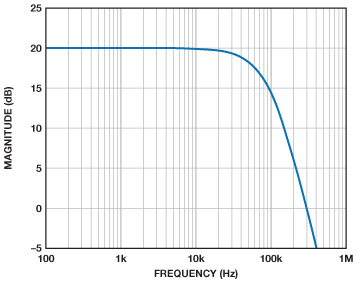
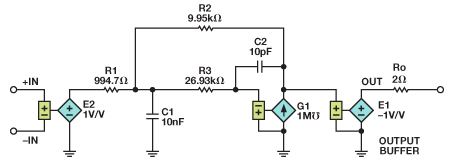
利用MFB拓撲可以進行相似的推導。網絡列表如下文所示,仿真模型則如圖14所示。
***AD8208 PREAMPLIFIER_TRANSFER_FUNCTION (GAIN = 20 dB)***
.SUBCKT 8208_MFB +IN –IN OUT
***G1 = VCCS WITH 120 dB OPEN_LOOP_GAIN***
G1 0 7 0 6 1E6
R1 4 3 994.7
R2 7 4 9.95K
R3 6 4 26.93K
C1 0 4 1N
C2 7 6 10P
EIN_STAGE 3 0 +IN –IN 1
***E2 = OUTPUT BUFFER***
E2 9 0 7 0 1
***OUTPUT RESISTANCE = 2 Ω***
RO OUT 9 2
.END
結束語
對于高帶寬放大器,與利用s域(拉普拉斯變換)傳遞函數相比,利用模擬元件構建SPICE模型能夠提供快得多的時域仿真。Sallen-Key和MFB低通濾波器拓撲提供了一種將s域傳遞函數轉換為電阻、電容和壓控電流源的方法。
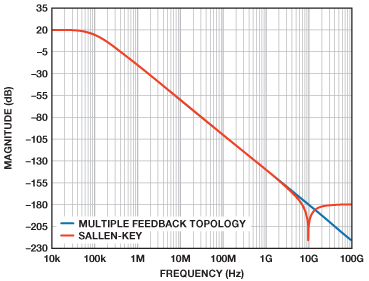
MFB拓撲的非理想操作來源于 C1 和 C2 在高頻時表現為相對于電阻R1、 R2和R3的阻抗短路。同樣,Sallen-Key拓撲的非理想操作來源于C1 和 C2 在高頻時表現為相對于電阻 R1 和 R2的阻抗短路。這兩種拓撲的對比如圖15所示。
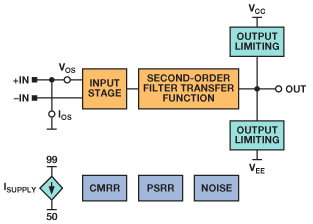
現有常用于CMRR、PSRR、失調電壓、電源電流、頻譜噪聲、輸入/輸出限幅及其它參數的電路可以與該模型合并,如圖16所示。
-
放大器
+關注
關注
143文章
13553瀏覽量
213116 -
仿真
+關注
關注
50文章
4044瀏覽量
133420 -
SPICE
+關注
關注
6文章
181瀏覽量
42517
發布評論請先 登錄
相關推薦
兼容SPICE的運算放大器宏模型
SPICE仿真模型的優點和缺點
用SPICE模型仿真失調電壓
ADS軟件導入spice模型仿真出現問題?
如何將放大器建模為模擬濾波器,從而提高SPICE仿真速度?
如何提高MPLAB X仿真速度?
如何用SPICE模型仿真失調電壓?
通過交互式SPICE仿真和分析各種放大器的設計
通過SPICE交互式仿真探討運算放大器電路
Spice仿真器:仿真速度和容量的提升
LTspice IV高性能Spice III仿真器應用程序免費下載




 放大器仿真模型可提高SPICE仿真速度
放大器仿真模型可提高SPICE仿真速度
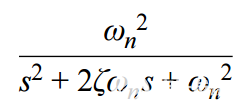










評論