【導語】用深度學習預測股票價格不是一個新話題，隨著技術的不斷發展，大家一直在不斷嘗試新技術。這次教程中，作者設計了一個強強聯合型模型來預測股票價格，為什么這么形容？作者設計了一個 GAN 模型，其生成網絡為 LSTM 模型用來預測時間序列數據、CNN 模型作判別網絡，用 BERT 模型作為情緒分析模型。帶有高斯過程的貝葉斯優化和深度強化學習方法來獲得 GAN 的超參數。為什么創建這樣的組合？都將在下面的內容中為大家進行一一解答。

這篇教程的篇幅很長，為了讓大家能對重要技術內容一目了然，作者在開始加入了層級清晰的目錄，主要從【背景】、【數據特征】、【GAN 模型架構】、【超參數優化】等幾大方面進行全面講解。

下面營長對其中涉及的技術細節進行了編譯：

背景

在今天的任務中，預測的是高盛公司（本文中會簡稱為 GS）的股票變化趨勢，使用 2010 年 1 月 1 日至 2018 年 12 月 31 日的日收盤價作為訓練（七年）和測試（兩年）數據。

成功訓練一個 GAN 最棘手的部分是獲得正確的超參數。為此，作者使用 Bayesian optimisation（帶有高斯過程的貝葉斯優化）和用于決定何時以及如何改變 GAN 的超參數的深層強化學習（DRL），在創建強化學習過程中，將使用一些最新技術，如 RAINBOW 和 PPO。

此外，在模型中還使用許多不同類型的輸入數據。隨著股票的歷史交易數據和技術指標，設計了一些技術方法，如使用 NLP 中的 BERT 來創建情緒分析模型（作為基本面分析的來源），以及用傅立葉變換（Fourier transforms）提取總體趨勢方向、識別其他高級特征的棧式自動編碼器（ Stacked autoencoder）；采用特征投資組合尋找相關資產；采用 ARIMA 方法進行股票函數近似。實際上，這些技術都是為了盡可能多的獲取關于股票的信息、模式、依賴關系等等。

開發環境和框架選擇 MXNet 和其高級 API（Gluon）創建所有的神經網絡，并在多個 GPU 上進行訓練。

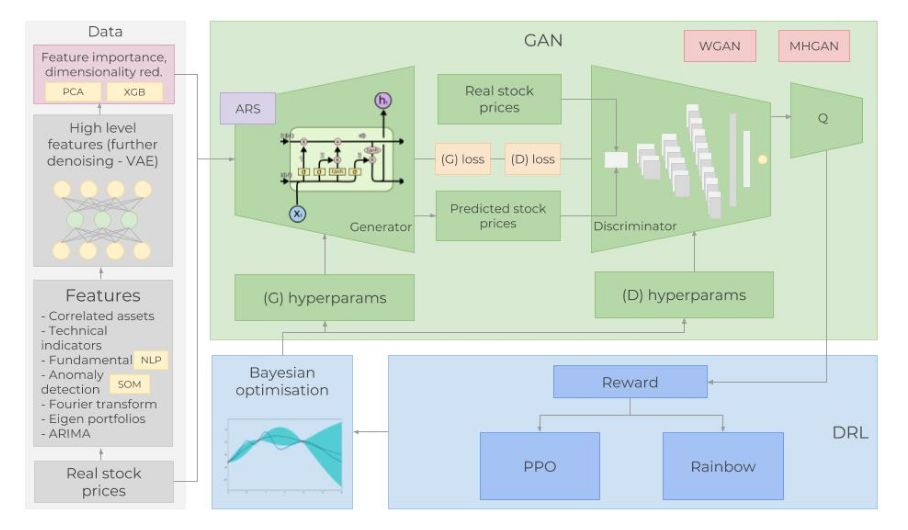
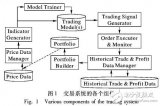
圖：完整體系結構概覽

通過上面的技術背景介紹，相信大家已經感覺到想準確預測股市是一項非常復雜的任務，影響股票變化的事件、條件或因素等實在是太多了。所以，想更好的了解這些先決條件，還需要先做幾個重要的假設：（1）市場不是 100% 的隨機；（2）歷史重復；（3）市場遵循人們的理性行為；（4）市場是“完美的”。

數據

首先，要了解什么因素會影響 GS 的股票價格波動，需要包含盡可能多的信息（從不同的方面和角度）。將使用 1585 天的日數據來訓練各種算法（70% 的數據），并預測另外 680 天的結果（測試數據）。然后，將預測結果與測試數據進行比較。每種類型的數據（亦稱為特征）將在后面的部分中詳細解釋。

簡而言之，將使用的特征有：

a.相關資產：涉及商品、外匯、指數、固定收益證券等各類資產數據；影響高盛公司股票價格趨勢的外部因素又有很多，并且很復雜，包括競爭對手、客戶、全球經濟、地緣政治形勢、財政和貨幣政策等等，這些因素還會相互產生影響。選擇合適的相關資產是非常重要的：

（1）首先是和 GS 相似的公司，如將摩根大通（JPMorgan Chase）和摩根士丹利（Morgan Stanley）等加入數據集。

（2）作為一家投資銀行，高盛依賴于全球經濟，需要關注全球經濟指數和 libor 利率。

（3）每日波動指數(VIX)。

（4）綜合指數，如 NASDAQ 和 NYSE（美國）、FTSE 100（英國）、日經指數 225（日本）、恒生指數和 BSE Sensex（APAC）指數。

（5）貨幣，全球貿易多次反映在貨幣流動中，使用一籃子貨幣（如美元-日元、英鎊-美元等）作為特征。

總的來說，在數據集中還有 72 個其他資產（每個資產的每日價格）。

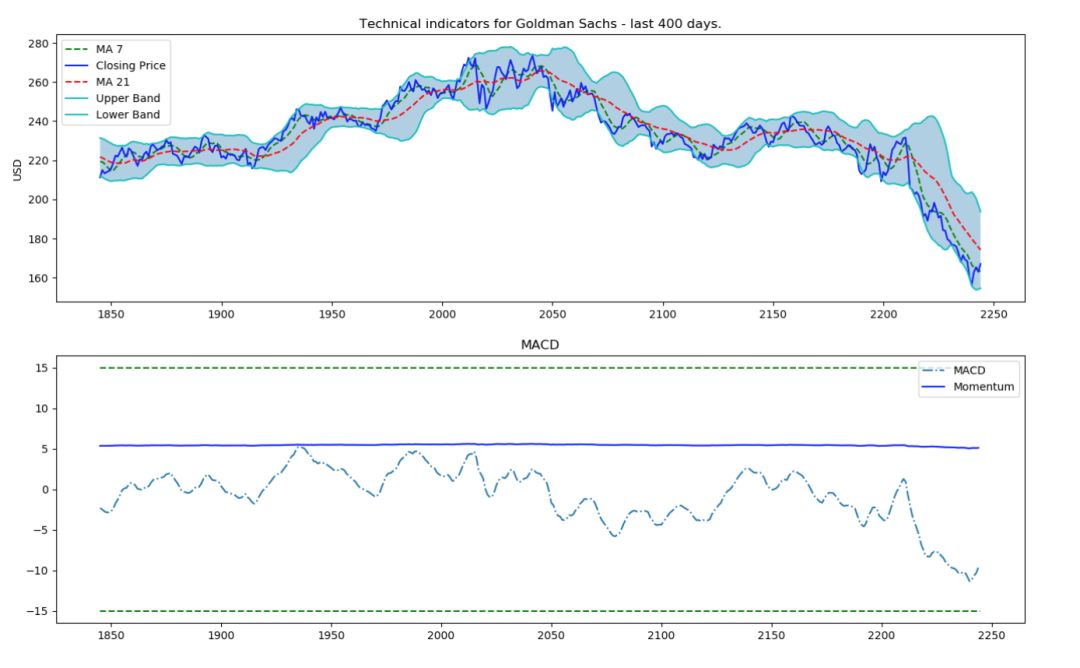
b.技術指標：許多投資人都會關注技術指標，在這里，把最受歡迎的指標作為獨立特征，包括 7 天和 21 天波動平均值、指數波動平均、Momentum、MACD 等 12項技術指標。

def get_technical_indicators(dataset): # Create 7 and 21 days Moving Average dataset['ma7'] = dataset['price'].rolling(window=7).mean() dataset['ma21'] = dataset['price'].rolling(window=21).mean() # Create MACD dataset['26ema'] = pd.ewma(dataset['price'], span=26) dataset['12ema'] = pd.ewma(dataset['price'], span=12) dataset['MACD'] = (dataset['12ema']-dataset['26ema']) # Create Bollinger Bands dataset['20sd'] = pd.stats.moments.rolling_std(dataset['price'],20) dataset['upper_band'] = dataset['ma21'] + (dataset['20sd']*2) dataset['lower_band'] = dataset['ma21'] - (dataset['20sd']*2) # Create Exponential moving average dataset['ema'] = dataset['price'].ewm(com=0.5).mean() # Create Momentum dataset['momentum'] = dataset['price']-1 return datasetdataset_TI_df = get_technical_indicators(dataset_ex_df[['GS']])dataset_TI_df.head()

c.基本面分析：無論股票漲跌，這都是一個非常重要的數據。分析時會用到兩個特征：公司業績報告和新聞將引導的一些趨勢，因此通過分析新聞來準確預測市場的情緒也是一項非常重要的工作，所以這次的方法中，將使用 BERT 來構建情緒分析模型，提取股票新聞中的情緒傾向。最后采用 sigmoid 歸一化，結果介于 0 到 1 之間，（0 表示負面情緒，1 表示正面情緒），每一天都會創建一個平均每日分數作為一個特征添加。

使用的是 MXNet 中 Gluon NLP 庫中所提供的經過預訓練的 BERT 模型，大家可以嘗試一下。此前我們也為大家介紹過簡單易上手的 Gluon，詳情可參考營長親自上手的教程。

d.傅里葉變換：利用每日收盤價，創建傅立葉變換，以獲得幾個長期和短期趨勢。使用這些變換消除大量的噪聲，獲得真實股票波動的近似值。有了趨勢近似，可以幫助 LSTM 網絡更準確地選擇其預測趨勢。

data_FT = dataset_ex_df[['Date', 'GS']]close_fft = np.fft.fft(np.asarray(data_FT['GS'].tolist()))fft_df = pd.DataFrame({'fft':close_fft})fft_df['absolute'] = fft_df['fft'].apply(lambda x: np.abs(x))fft_df['angle'] = fft_df['fft'].apply(lambda x: np.angle(x))plt.figure(figsize=(14, 7), dpi=100)fft_list = np.asarray(fft_df['fft'].tolist())for num_ in [3, 6, 9, 100]: fft_list_m10= np.copy(fft_list); fft_list_m10[num_:-num_]=0 plt.plot(np.fft.ifft(fft_list_m10), label='Fourier transform with {} components'.format(num_))plt.plot(data_FT['GS'], label='Real')plt.xlabel('Days')plt.ylabel('USD')plt.title('Figure 3: Goldman Sachs (close) stock prices & Fourier transforms')plt.legend()plt.show()

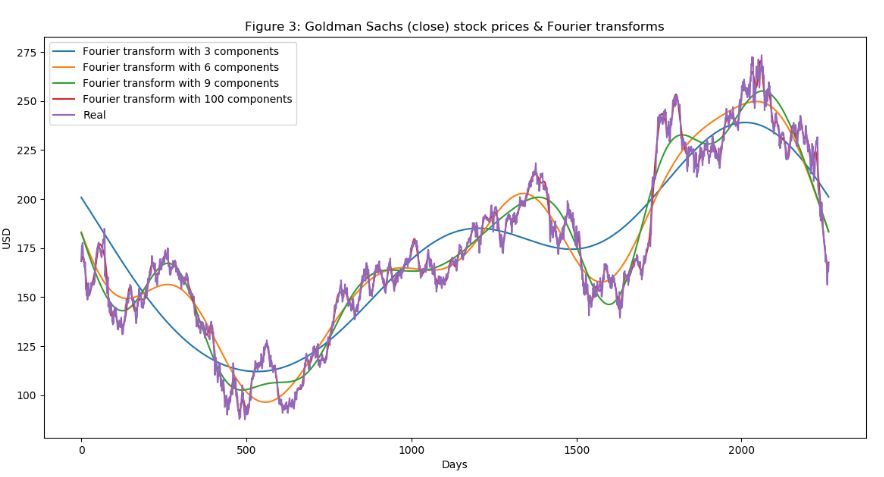
圖：高盛股票的傅里葉變換

e.ARIMA：這是預測時間序列數據未來值的最流行技術之一。

frompandasimportread_csvfrom pandas import datetimefrom statsmodels.tsa.arima_model import ARIMAfrom sklearn.metrics import mean_squared_errorX = series.valuessize = int(len(X) * 0.66)train, test = X[0:size], X[size:len(X)]history = [x for x in train]predictions = list()for t in range(len(test)): model = ARIMA(history, order=(5,1,0)) model_fit = model.fit(disp=0) output = model_fit.forecast() yhat = output[0] predictions.append(yhat) obs = test[t] history.append(obs)error = mean_squared_error(test, predictions)print('Test MSE: %.3f' % error)Test MSE: 10.151# Plot the predicted (from ARIMA) and real pricesplt.figure(figsize=(12, 6), dpi=100)plt.plot(test, label='Real')plt.plot(predictions, color='red', label='Predicted')plt.xlabel('Days')plt.ylabel('USD')plt.title('Figure 5: ARIMA model on GS stock')plt.legend()plt.show

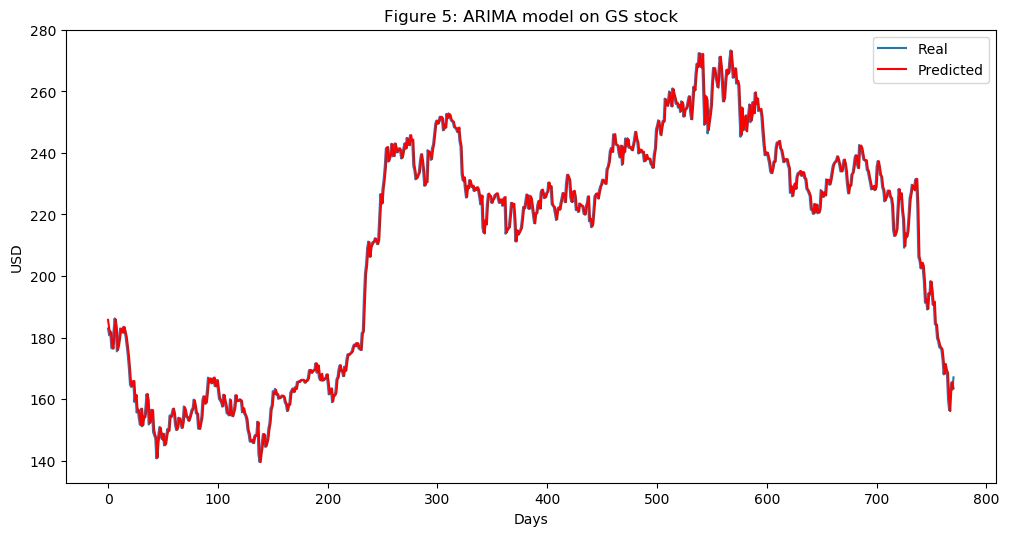
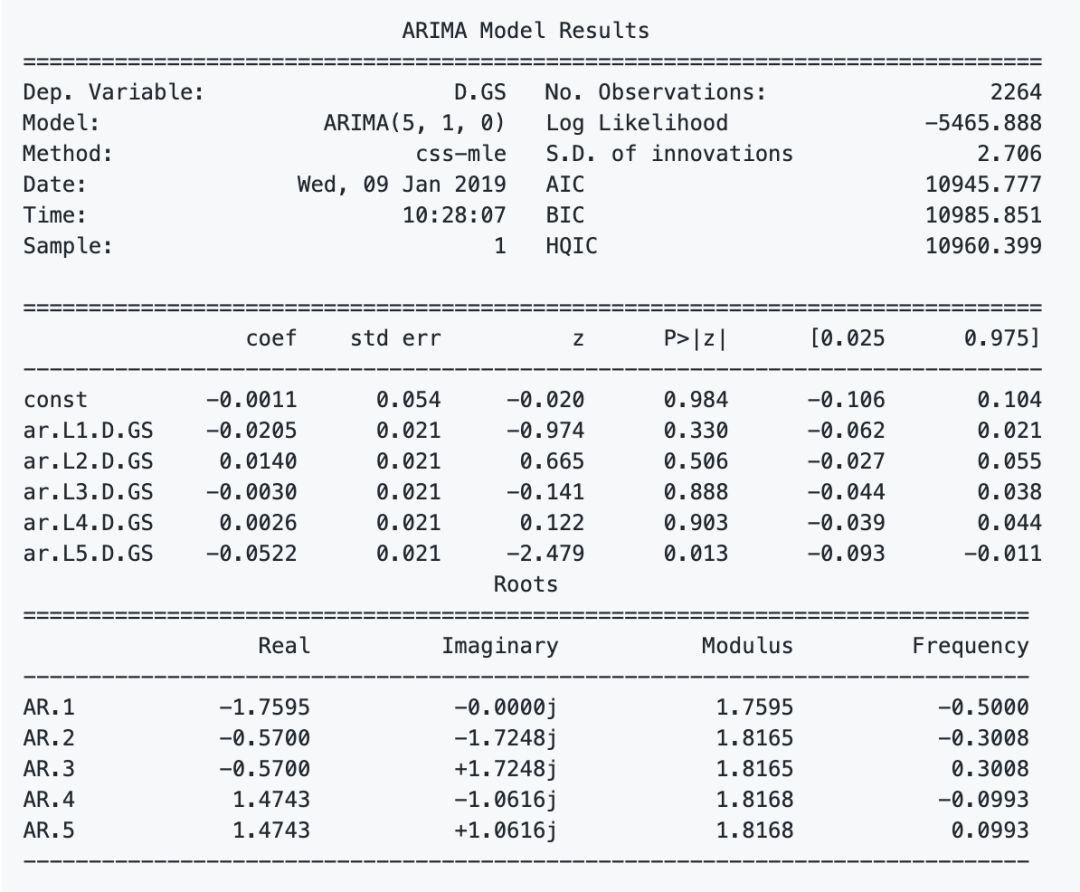
f.Stacked autoencoders?（棧式自動編碼器）：上面提到的一些特征是研究人員經過幾十年的研究發現的，但是還是會忽視一些隱藏的關聯特征，由此，Stacked autoencoders? 就可以解決這個問題，通過學習每個隱藏層，發現更多新特征（可能有些是我們無法發現，理解的）。這次沒有把 RELU 作為激活函數，而是使用了 GELU，也可以用于 BERT 模型中。至于為什么選擇 GELU，大家可以在原文中看到作者給出的和 RELU 對比的實例。

g.深度無監督學習：用于期權定價中的異常檢測，將再使用一個特征：每天都會增加高盛股票90天看漲期權的價格。期權定價本身結合了很多數據。期權合約的價格取決于股票的未來價值(分析師也試圖預測價格，以便為看漲期權得出最準確的價格)。使用深度無監督學習(自組織映射)，嘗試發現出現異常的每日價格。異常(如價格的劇烈變化)可能表明出現了一個事件，這有助于LSTM了解整體股票模式。

from utils import *import timeimport numpy as npfrom mxnet import nd, autograd, gluonfrom mxnet.gluon import nn, rnnimport mxnet as mximport datetimeimportseabornassnsimport matplotlib.pyplot as plt%matplotlib inlinefrom sklearn.decomposition import PCAimport mathfrom sklearn.preprocessing import MinMaxScalerfrom sklearn.metrics import mean_squared_errorfrom sklearn.preprocessing import StandardScalerimport xgboost as xgbfrom sklearn.metrics import accuracy_scoreimport warningswarnings.filterwarnings("ignore")context = mx.cpu(); model_ctx=mx.cpu()mx.random.seed(1719)Note: The purpose of this section (3. The Data) is to show the data preprocessing and to give rationale for using different sources of data, hence I will only use a subset of the full data (that is used for training).def parser(x): return datetime.datetime.strptime(x,'%Y-%m-%d')dataset_ex_df = pd.read_csv('data/panel_data_close.csv', header=0, parse_dates=[0], date_parser=parser)dataset_ex_df[['Date','GS']].

接下來，有了這么多特征，還需要執行幾個重要步驟：

h.對數據的“質量”進行統計檢查：確保數據質量對模型來說非常重要，因此要執行以下幾個簡單的檢驗，如異方差、多重共線性、Serial correlation 等。

i.確定特征重要性：采用 XGBoost 算法。這么多的特征，必須考慮是否所有這些都真正地指示了 GS 股票波動方向。例如，數據集中包括其變化可能意味著經濟變化的 LIBOR，而這又可能暗示 GS 股票將會發生波動，因此需要對此預測進行測試，在眾多的測試方法中，本教程中選擇了 XGBoost，其在分類和回歸問題上都提供了很好的結果。

defget_feature_importance_data(data_income): data = data_income.copy() y = data['price'] X = data.iloc[:, 1:] train_samples = int(X.shape[0] * 0.65) X_train = X.iloc[:train_samples] X_test = X.iloc[train_samples:] y_train = y.iloc[:train_samples] y_test = y.iloc[train_samples:] return (X_train, y_train), (X_test, y_test)# Get training and test data(X_train_FI, y_train_FI), (X_test_FI, y_test_FI) = get_feature_importance_data(dataset_TI_df)regressor = xgb.XGBRegressor(gamma=0.0,n_estimators=150,base_score=0.7,colsample_bytree=1,learning_rate=0.05)xgbModel = regressor.fit(X_train_FI,y_train_FI, \ eval_set = [(X_train_FI, y_train_FI), (X_test_FI, y_test_FI)], \ verbose=False)eval_result = regressor.evals_result()training_rounds=range(len(eval_result['validation_0']['rmse']))

最后一步，使用主成分分析（PCA）創建特征組合，以減少自動編碼器生成特征的維數。在自動編碼器中創建了 112 個特征，不過高維特征對我們的價值更大，所以在這 112 個特征的基礎上通過 PCA 創建高維的特征組合，減少數據維度。不過，這也是我們提出的實驗性方法。

plt.figure(figsize=(15, 5))plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=.5, hspace=None)ranges_ = (-10, 3, .25)plt.subplot(1, 2, 1)plt.plot([i for i in np.arange(*ranges_)], [relu(i) for i in np.arange(*ranges_)], label='ReLU', marker='.')plt.plot([i for i in np.arange(*ranges_)], [gelu(i) for i in np.arange(*ranges_)], label='GELU')plt.hlines(0, -10, 3, colors='gray', linestyles='--', label='0')plt.title('Figure 7: GELU as an activation function for autoencoders')plt.ylabel('f(x) for GELU and ReLU')plt.xlabel('x')plt.legend()plt.subplot(1, 2, 2)plt.plot([i for i in np.arange(*ranges_)], [lrelu(i) for i in np.arange(*ranges_)], label='Leaky ReLU')plt.hlines(0, -10, 3, colors='gray', linestyles='--', label='0')plt.ylabel('f(x) for Leaky ReLU')plt.xlabel('x')plt.title('Figure 8: LeakyReLU')plt.legend()plt.sho

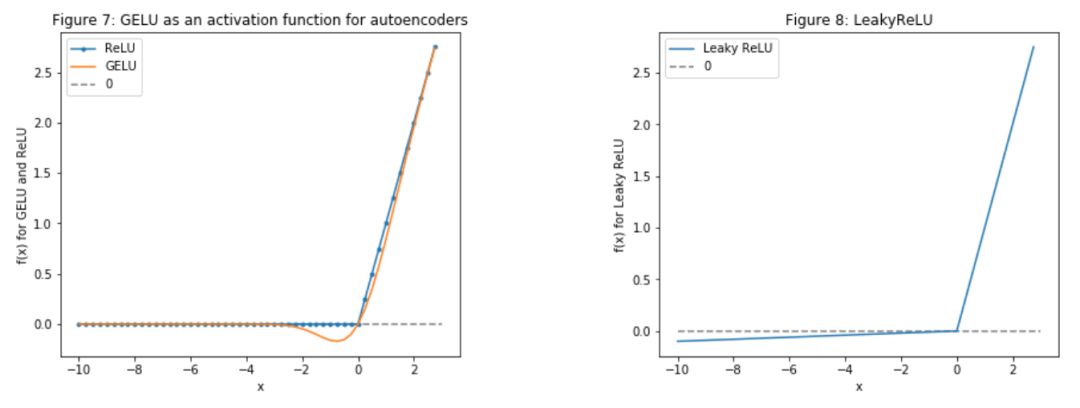
讓我們看一下過去 9 年的股價變化。虛線表示訓練數據和測試數據之間的分割線。

plt.figure(figsize=(14, 5), dpi=100)plt.plot(dataset_ex_df['Date'], dataset_ex_df['GS'], label='Goldman Sachs stock')plt.vlines(datetime.date(2016,4, 20), 0, 270, linestyles='--', colors='gray', label='Train/Test data cut-off')plt.xlabel('Date')plt.ylabel('USD')plt.title('Figure 2: Goldman Sachs stock price')plt.legend()plt.show()

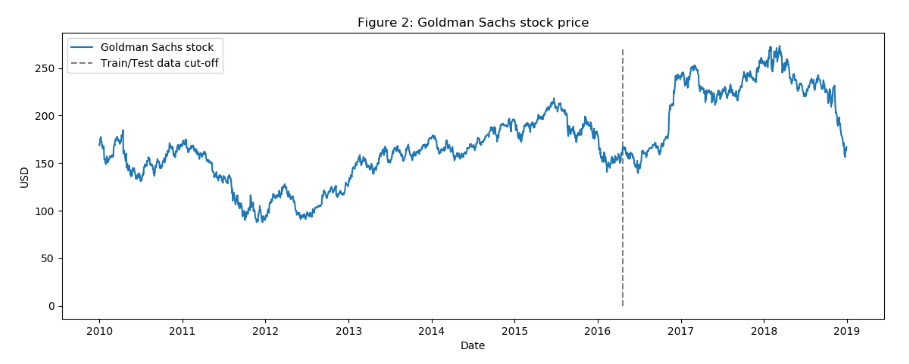
圖：過去9年高盛股價的波動

num_training_days = int(dataset_ex_df.shape[0]*.7)print('Number of training days: {}. Number of test days: {}.'.format(num_training_days, \ dataset_ex_df.shape[0]-num_training_days))Numberoftrainingdays:1585.Numberoftestdays:680.

生成對抗性網絡(GAN)

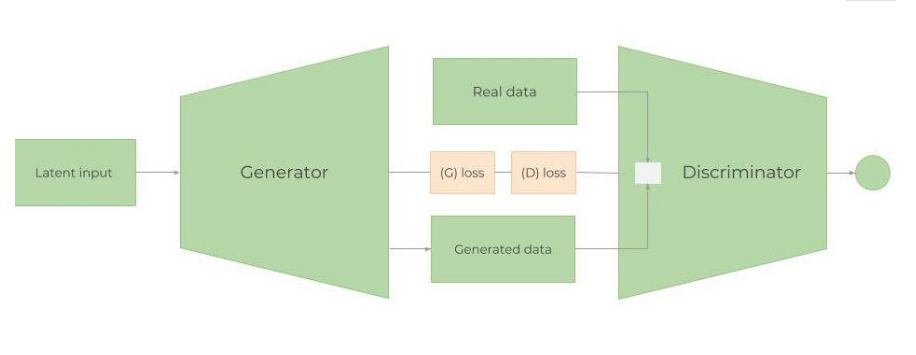
圖：GAN 架構

1、為什么采用GAN進行股市預測？

GAN 最多被應用在創作逼真的圖像、畫作和視頻剪輯等。對預測時間序列數據的應用并不多。但這兩者的思想都是類似的。我們希望預測未來的股票價格，GS 的股票波動和行為應該大致相同(除非開始以完全不同的方式運作，或者經濟急劇變化)。因此，希望“生成”的數據與已經擁有的歷史交易數據分布相似，當然不是完全相同。在這個例子中將使用 LSTM 作為時間序列生成模型，CNN 作為判別模型。

2、Metropolis-Hastings GAN 和 Wasserstein GAN

（1）Metropolis-Hastings GAN：與傳統的 GAN 相比，Uber 團隊最近提出一種新改進的 GAN 模型——Metropolis-Hastings GAN （MHGAN），它有點類似于谷歌和加州大學伯克利分校提出的Discriminator Rejection Sampling。通常情況下，在訓練完GAN之后就不再使用 D 了。然而，MHGAN 和 DRS 試圖使用 D 來選擇由 G 生成的接近真實的樣本。

（2）Wasserstein GAN：訓練 GAN 是相當困難的。模型可能永遠不會收斂，模式崩潰也很容易發生。，通過 Wasserstein GAN 嘗試解決這個問題。KL 距離和 JS 距離是兩種常用的分布，而 WGAN 使用的是 Wasserstein distanc。

3、生成模型：單層RNN

（1）LSTM 還是 GRU？

關于 RNN、LSTM 等模型的基礎介紹這里不多做贅述，主要聚焦在 RNN 在時間序列數據上的應用，因為它們可以跟蹤所有以前的數據點，并且可以捕獲經過時間發展的模式。可以通過裁剪解 RNN 梯度消失或梯度爆炸問題。

在精度方面，LSTM 和 GRU 的結果相差不多，但是 GRU 使用的訓練參數要比 LSTM 少，計算強度也要小。

（2）LSTM 體系結構

LSTM架構非常簡單：一個LSTM層，包含112個輸入單元(數據集中有112個特征)和500個隱藏單元；一個以每日股價為輸出的 Dense 層；采用 Xavier 初始化，使用 L1 損失函數

在下面的代碼中，采用adam作為優化器，學習率為 0.01。

gan_num_features = dataset_total_df.shape[1]sequence_length = 17class RNNModel(gluon.Block): def __init__(self, num_embed, num_hidden, num_layers, bidirectional=False, \ sequence_length=sequence_length, **kwargs): super(RNNModel, self).__init__(**kwargs) self.num_hidden = num_hidden with self.name_scope(): self.rnn = rnn.LSTM(num_hidden, num_layers, input_size=num_embed, \ bidirectional=bidirectional, layout='TNC') self.decoder = nn.Dense(1, in_units=num_hidden) def forward(self, inputs, hidden): output, hidden = self.rnn(inputs, hidden) decoded = self.decoder(output.reshape((-1, self.num_hidden))) return decoded, hidden def begin_state(self, *args, **kwargs): return self.rnn.begin_state(*args, **kwargs)lstm_model = RNNModel(num_embed=gan_num_features, num_hidden=500, num_layers=1)lstm_model.collect_params().initialize(mx.init.Xavier(), ctx=mx.cpu())trainer = gluon.Trainer(lstm_model.collect_params(), 'adam', {'learning_rate': .01})loss=glu

（3）學習率調度器

學習率是非常重要的參數之一，每個優化器設置學習率，如 SGD、Adam 或 RMSProp 在訓練神經網絡時至關重要，因為它既控制著網絡的收斂速度，又控制著網絡的最終性能，接下來就要確定每個階段的學習率。

classTriangularSchedule(): def __init__(self, min_lr, max_lr, cycle_length, inc_fraction=0.5): self.min_lr = min_lr self.max_lr = max_lr self.cycle_length = cycle_length self.inc_fraction = inc_fraction def __call__(self, iteration): if iteration <= self.cycle_length*self.inc_fraction: unit_cycle = iteration * 1 / (self.cycle_length * self.inc_fraction) elif iteration <= self.cycle_length: unit_cycle = (self.cycle_length - iteration) * 1 / (self.cycle_length * (1 - self.inc_fraction)) else: unit_cycle = 0 adjusted_cycle = (unit_cycle * (self.max_lr - self.min_lr)) + self.min_lr return adjusted_cycleclass CyclicalSchedule(): def __init__(self, schedule_class, cycle_length, cycle_length_decay=1, cycle_magnitude_decay=1, **kwargs): self.schedule_class = schedule_class self.length = cycle_length self.length_decay = cycle_length_decay self.magnitude_decay = cycle_magnitude_decay self.kwargs = kwargs def __call__(self, iteration): cycle_idx = 0 cycle_length = self.length idx = self.length while idx <= iteration: cycle_length = math.ceil(cycle_length * self.length_decay) cycle_idx += 1 idx += cycle_length cycle_offset = iteration - idx + cycle_length schedule = self.schedule_class(cycle_length=cycle_length,**self.kwargs)????????return?schedule(cycle_offset)?*self.magnitude_decay**cycle_idx

（4）防止過擬合與偏差-方差權衡

防止過擬合，注意總損失也是要在訓練模型中非常重要的一個問題。不僅在生成器中的 LSTM 模型，判別器中的 CNN 模型、自動編碼器中都使用了幾種防止過擬合的技術：

a.確保數據質量

b.正則化，或權重懲罰：最常用的兩種正則化技術是L1 和 L2 正則法。L1對離散值更有魯棒性，當數據稀疏時使用，可得到特征重要性。因此，在股票價格預測這個應用案例中將使用 L1 正則法。

c.Dropout。Dropout層隨機刪除隱藏層中的節點。

d.Dense-sparse-dense training

e.提前停止.

（5）權衡偏差-方差

建立復雜神經網絡時，另一個重要的考慮因素是偏差-方差權衡。訓練網絡的誤差基本上是偏差、方差和不可約誤差 σ(噪聲和隨機性引起的誤差)的函數。

最簡單的權衡公式是：誤差=偏差^2+方差+σ.

a.偏差（Bias）：偏差衡量一個經過訓練的（訓練數據集）算法對未見數據的概括能力。高偏差(欠擬合)意味著模型在隱藏數據上不能很好地工作。

b.方差（Variance）：方差衡量模型對數據集變化的敏感性。高方差意味著過擬合。

4、 一維 CNN 判別模型

（1）為何采用CNN作為判別模型？

CNN 網絡在提取隱藏特征等工作上具有優勢，那如何應用于這個任務中？大家不妨嘗試一下，數據點行程小趨勢，小趨勢行程大趨勢，趨勢反之形成模式，而 CNN 在此用檢測特征的能力來提取 GS 股價趨勢中的模式信息。

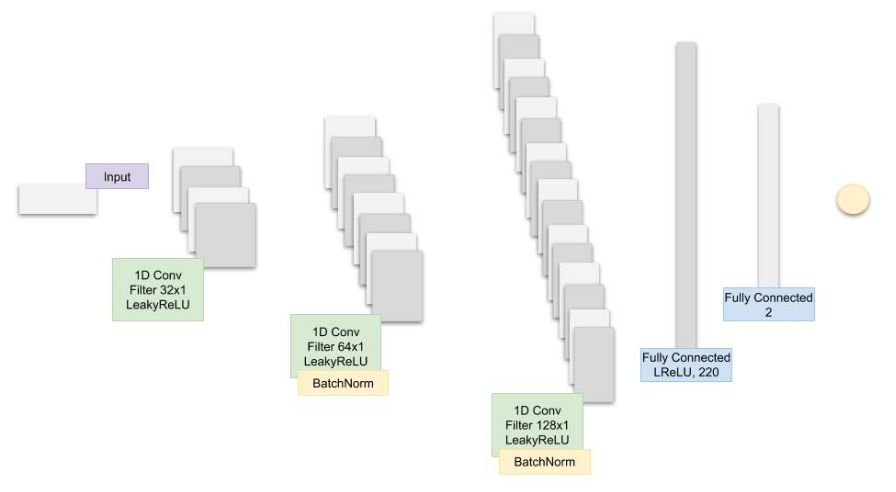
圖：本文提出的 CNN 模型的體系結構。

超參數優化

（1）跟蹤和優化的超參數是：

batch_size：LSTM 和 CNN 的 Batch 大小

cnn_lr：CNN 的學習率

strides：CNN 的跨步卷積數

lrelu_alpha：GAN 中 LeakyReLU 的 Alpha 值

batchnorm_momentum：CNN Batch 正則化的 momentum

padding：CNN 中的 Padding

kernel_size：1 CNN 的內核大小

dropout：LSTM 中的 Dropout 層

filters：過濾器的初始數目

epoch = 200

（2）超參數優化

經過 200 次 GAN 訓練后，將記錄 MAE（LSTM、GG 中的誤差函數）并作為獎勵值傳遞給強化學習（RL）模型，以決定是否用同一組超參數來改變保持訓練的超參數，如果RL決定更新超參數，它將調用 Bayes 優化庫。

（3）超參數優化中的強化學習

為什么在超參數優化中使用強化學習？股票市場一直在變化。即使能夠訓練 GAN 和 LSTM 來創造非常精確的結果，結果也只能在一定的時間內有效。也就是說，我們需要不斷優化整個過程。為了優化這一過程，可以添加或刪除特征，或改進深度學習模型。改進模型的最重要的方法之一就是通過超參數。一旦找到了一組特定的超參數，就需要決定何時修改它們，以及何時使用已經知道的集合(探索或利用)。此外，股票市場代表了一個依賴于數百萬參數的連續空間。

（4）強化學習理論

使用無模型的 RL 算法，原因很明顯，我們不知道整個環境，因此沒有關于環境如何工作的定義模型（如果存在，就不需要預測股票價格的變化）。使用兩個細分的無模型RL：策略優化（Policy Optimization）和 Q-Learning。構建 RL 算法的一個關鍵方面是精確設置獎勵。它必須捕捉環境的所有方面以及代理與環境的交互。

a.Q-Learning：一種基于Q-Learning的非策略深度強化學習算法，它將7種算法結合在一起：DQN、Double Q Learning（雙QL）、Prioritized replay、決斗網絡(Dueling networks)、多步學習、分布式RL、噪聲網絡（Noisy Nets）。在Q-Learning中，學習價值從某一狀態采取行動。Q 值采取行動后的預期回報。

b.策略優化：這里采用近端策略優化（Proximal Policy Optimization, PPO），在決策優化中，學習從某一狀態采取的行動。(如果使用諸如Actor/Critic之類的方法，也會了解處于給定狀態的價值。

（5）貝葉斯優化

使用貝葉斯優化，不采用網格搜索，因為可能需要很長時間才能找到超參數的最佳組合。

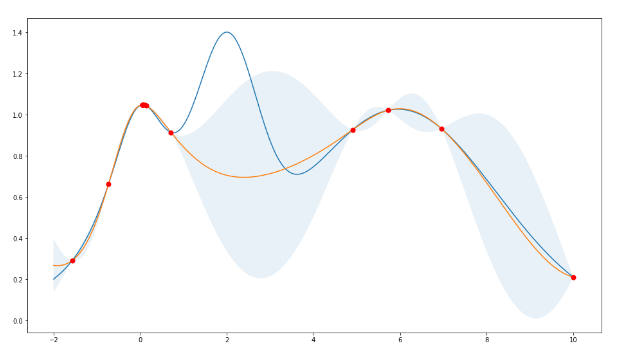
圖：貝葉斯超參數優化的高斯過程

5、結果

最后，使用測試數據作為不同階段的輸入，LSTM 的輸出與實際股價進行比較：

（1）繪制第一次訓練之后的結果

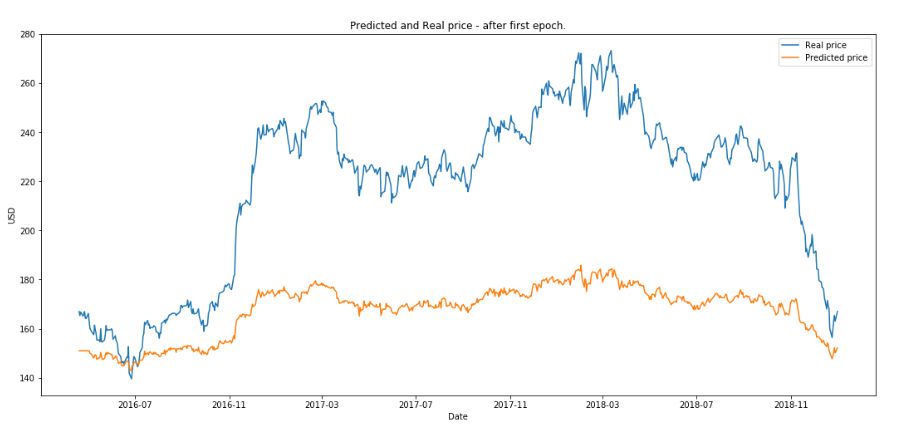
（2）繪制 50 次訓練后的結果。

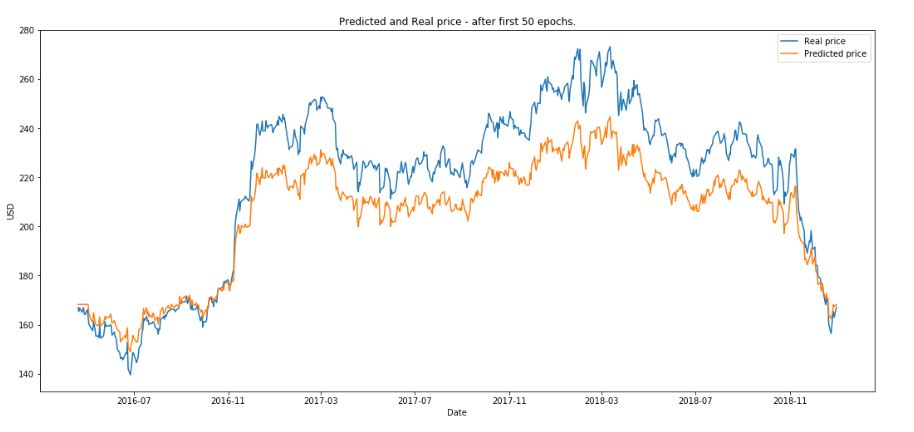
（3）繪制 200 次訓練后的結果。

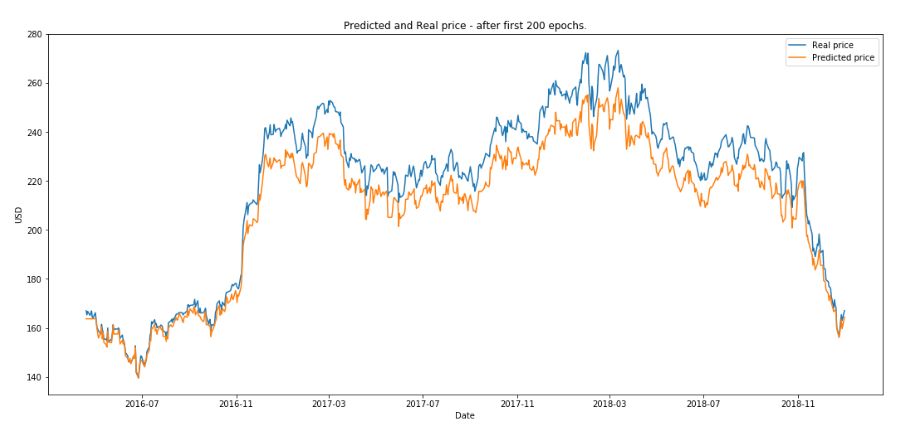
RL 運行了 10 eposide ，本文定義一個 eposide 是 GAN 完整訓練 200 次后，下圖是得到的最終的結果。

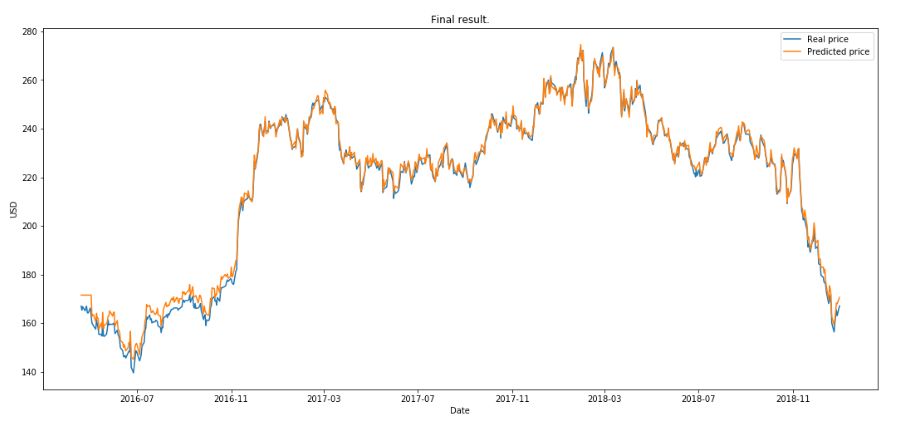
總結

可見，作者在把各路強模型聯合打造的結果還是非常優秀的。不過作者還嘗試創建一個 RL 環境，用于測試決定何時以及如何進行交易的交易算法。GAN 的輸出將是此環境中的一個參數，雖然這些都不能完全做到預測的作用，但是在實際任務中不斷嘗試新技術還是很有意義的，期待作者后續工作可以帶來更好的結果。