統(tǒng)計學和機器學習之間的界定一直很模糊。

無論是業(yè)界還是學界一直認為機器學習只是統(tǒng)計學批了一層光鮮的外衣。

而機器學習支撐的人工智能也被稱為“統(tǒng)計學的外延”

例如，諾獎得主托馬斯·薩金特曾經(jīng)說過人工智能其實就是統(tǒng)計學，只不過用了一個很華麗的辭藻。

薩金特在世界科技創(chuàng)新論壇上表示，人工智能其實就是統(tǒng)計學

當然也有一些不同的聲音。但是這一觀點的正反雙方在爭吵中充斥著一堆看似高深實則含糊的論述，著實讓人摸不著頭腦。

一位名叫Matthew Stewart的哈佛大學博士生從統(tǒng)計與機器學習的不同；統(tǒng)計模型與機器學習的不同，這兩個角度論證了機器學習和統(tǒng)計學并不是互為代名詞。

機器學習和統(tǒng)計的主要區(qū)別在于它們的目的

與大部分人所想的正相反，機器學習其實已經(jīng)存在幾十年了。當初只是因為那時的計算能力無法滿足它對大量計算的需求，而漸漸被人遺棄。然而，近年來，由于信息爆炸所帶來的數(shù)據(jù)和算力優(yōu)勢，機器學習正快速復蘇。

言歸正傳，如果說機器學習和統(tǒng)計學是互為代名詞，那為什么我們沒有看到每所大學的統(tǒng)計學系都關門大吉而轉投'機器學習'系呢？因為它們是不一樣的!

我經(jīng)常聽到一些關于這個話題的含糊論述，最常見的是這樣的說法:

"機器學習和統(tǒng)計的主要區(qū)別在于它們的目的。機器學習模型旨在使最準確的預測成為可能。統(tǒng)計模型是為推斷變量之間的關系而設計的。

雖然技術上來說這是正確的，但這樣的論述并沒有給出特別清晰和令人滿意的答案。機器學習和統(tǒng)計之間的一個主要區(qū)別確實是它們的目的。

然而，說機器學習是關于準確的預測，而統(tǒng)計模型是為推理而設計，幾乎是毫無意義的說法，除非你真的精通這些概念。

首先，我們必須明白，統(tǒng)計和統(tǒng)計建模是不一樣的。統(tǒng)計是對數(shù)據(jù)的數(shù)學研究。除非有數(shù)據(jù)，否則無法進行統(tǒng)計。統(tǒng)計模型是數(shù)據(jù)的模型，主要用于推斷數(shù)據(jù)中不同內(nèi)容的關系，或創(chuàng)建能夠預測未來值的模型。通常情況下，這兩者是相輔相成的。

因此，實際上我們需要從兩方面來論述：第一，統(tǒng)計與機器學習有何不同；第二，統(tǒng)計模型與機器學習有何不同？

說的更直白些就是，有很多統(tǒng)計模型可以做出預測，但預測效果比較差強人意。

而機器學習通常會犧牲可解釋性以獲得強大的預測能力。例如，從線性回歸到神經(jīng)網(wǎng)絡，盡管解釋性變差，但是預測能力卻大幅提高。

從宏觀角度來看，這是一個很好的答案。至少對大多數(shù)人來說已經(jīng)足夠好。然而，在有些情況下，這種說法容易讓我們對機器學習和統(tǒng)計建模之間的差異產(chǎn)生誤解。讓我們看一下線性回歸的例子。

統(tǒng)計模型與機器學習在線性回歸上的差異

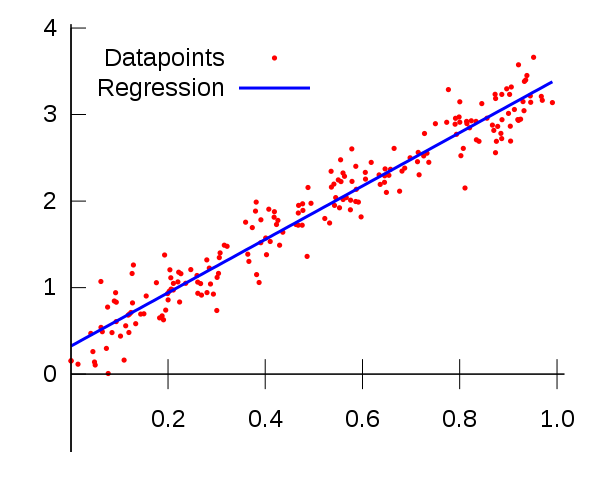
或許是因為統(tǒng)計建模和機器學習中使用方法的相似性，使人們認為它們是同一個東西。對這我可以理解，但事實上不是這樣。

最明顯的例子是線性回歸，這可能是造成這種誤解的主要原因。線性回歸是一種統(tǒng)計方法，通過這種方法我們既可以訓練一個線性回歸器，又可以通過最小二乘法擬合一個統(tǒng)計回歸模型。

可以看到，在這個案例中，前者做的事兒叫"訓練"模型，它只用到了數(shù)據(jù)的一個子集，而訓練得到的模型究竟表現(xiàn)如何需要通過數(shù)據(jù)的另一個子集測試集測試之后才能知道。在這個例子中，機器學習的最終目的是在測試集上獲得最佳性能。

對于后者，我們則事先假設數(shù)據(jù)是一個具有高斯噪聲的線性回歸量，然后試圖找到一條線，最大限度地減少了所有數(shù)據(jù)的均方誤差。不需要訓練或測試集，在許多情況下，特別是在研究中(如下面的傳感器示例)，建模的目的是描述數(shù)據(jù)與輸出變量之間的關系, 而不是對未來數(shù)據(jù)進行預測。我們稱此過程為統(tǒng)計推斷，而不是預測。盡管我們可以使用此模型進行預測，這也可能是你所想的，但評估模型的方法不再是測試集，而是評估模型參數(shù)的顯著性和健壯性。

機器學習（這里特指有監(jiān)督學習）的目的是獲得一個可反復預測的模型。我們通常不關心模型是否可以解釋。機器學習只在乎結果。就好比對公司而言，你的價值只用你的表現(xiàn)來衡量。而統(tǒng)計建模更多的是為了尋找變量之間的關系和確定關系的顯著性，恰巧迎合了預測。

下面我舉一個自己的例子，來說明兩者的區(qū)別。我是一名環(huán)境科學家。工作的主要內(nèi)容是和傳感器數(shù)據(jù)打交道。如果我試圖證明傳感器能夠?qū)δ撤N刺激(如氣體濃度)做出反應, 那么我將使用統(tǒng)計模型來確定信號響應是否具有統(tǒng)計顯著性。我會嘗試理解這種關系，并測試其可重復性，以便能夠準確地描述傳感器的響應，并根據(jù)這些數(shù)據(jù)做出推斷。我還可能測試，響應是否是線性的？響應是否歸因于氣體濃度而不是傳感器中的隨機噪聲？等等。

而同時，我也可以拿著從20個不同傳感器得到的數(shù)據(jù), 去嘗試預測一個可由他們表征的傳感器的響應。如果你對傳感器了解不多，這可能會顯得有些奇怪，但目前這確實是環(huán)境科學的一個重要研究領域。

用一個包含20個不同變量的模型來表征傳感器的輸出顯然是一種預測，而且我也沒期待模型是可解釋的。要知道，由于化學動力學產(chǎn)生的非線性以及物理變量與氣體濃度之間的關系等等因素，可能會使這個模型非常深奧，就像神經(jīng)網(wǎng)絡那樣難以解釋。盡管我希望這個模型能讓人看懂, 但其實只要它能做出準確的預測，我就相當高興了。

如果我試圖證明數(shù)據(jù)變量之間的關系在某種程度上具有統(tǒng)計顯著性，以便我可以在科學論文中發(fā)表，我將使用統(tǒng)計模型而不是機器學習。這是因為我更關心變量之間的關系，而不是做出預測。做出預測可能仍然很重要，但是大多數(shù)機器學習算法缺乏可解釋性，這使得很難證明數(shù)據(jù)中存在的關系。

很明顯，這兩種方法在目標上是不同的，盡管使用了相似的方法來達到目標。機器學習算法的評估使用測試集來驗證其準確性。然而，對于統(tǒng)計模型，通過置信區(qū)間、顯著性檢驗和其他檢驗對回歸參數(shù)進行分析，可以用來評估模型的合法性。因為這些方法產(chǎn)生相同的結果，所以很容易理解為什么人們會假設它們是相同的。

統(tǒng)計與機器學習在線性回歸上的差異

有一個誤解存在了10年：僅基于它們都利用相同的基本概率概念這一事實，來混淆這兩個術語是不合理的。

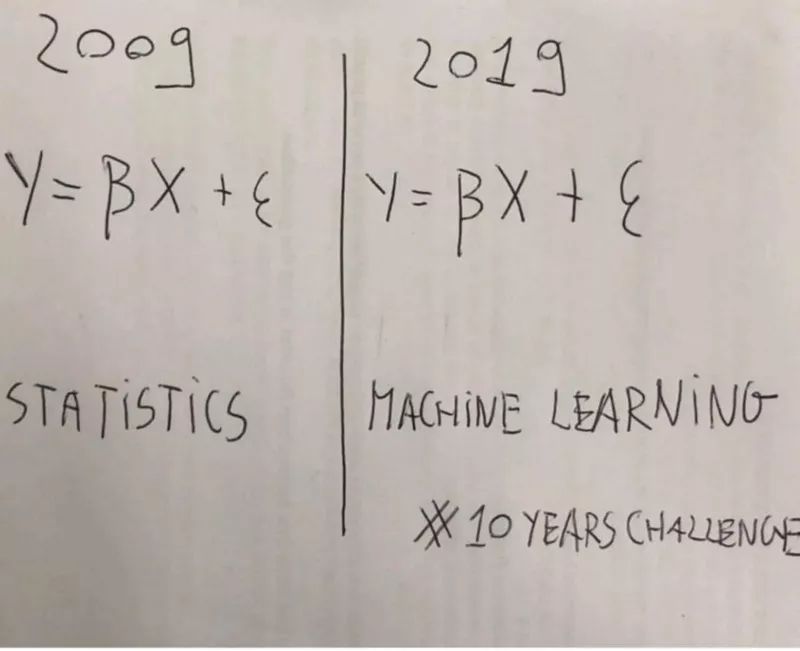
然而，僅僅基于這兩個術語都利用了概率里相同的基本概念這一事實而將他們混為一談是不合理的。就好比，如果我們僅僅把機器學習當作皮了一層光鮮外衣的統(tǒng)計，我們也可以這樣說：

物理只是數(shù)學的一種更好聽的說法。

動物學只是郵票收藏的一種更好聽的說法。

建筑學只是沙堡建筑的一種更好聽的說法。

這些說法（尤其是最后一個）非常荒謬，完全混淆了兩個類似想法的術語。

實際上，物理是建立在數(shù)學基礎上的，理解現(xiàn)實中的物理現(xiàn)象是數(shù)學的應用。物理學還包括統(tǒng)計學的各個方面，而現(xiàn)代統(tǒng)計學通常是建立在Zermelo-Frankel集合論與測量理論相結合的框架中，以產(chǎn)生概率空間。它們有很多共同點，因為它們來自相似的起源，并運用相似的思想得出一個邏輯結論。同樣，建筑學和沙堡建筑可能有很多共同點，但即使我不是一個建筑師，也不能給出一個清晰的解釋，但也看得出它們顯然不一樣。

在我們進一步討論之前，需要簡要澄清另外兩個與機器學習和統(tǒng)計有關的常見誤解。這就是人工智能不同于機器學習，數(shù)據(jù)科學不同于統(tǒng)計學。這些都是沒有爭議的問題，所以很快就能說清楚。

數(shù)據(jù)科學本質(zhì)上是應用于數(shù)據(jù)的計算和統(tǒng)計方法，包括小數(shù)據(jù)集或大數(shù)據(jù)集。它也包括諸如探索性數(shù)據(jù)分析之類的東西，例如對數(shù)據(jù)進行檢查和可視化，以幫助科學家更好地理解數(shù)據(jù)，并從中做出推論。數(shù)據(jù)科學還包括諸如數(shù)據(jù)包裝和預處理之類的東西，因此涉及到一定程度的計算機科學，因為它涉及編碼和建立數(shù)據(jù)庫、Web服務器之間的連接和流水線等等。

要進行統(tǒng)計，你并不一定得依靠電腦，但如果是數(shù)據(jù)科學缺了電腦就沒法操作了。這就再次說明了雖然數(shù)據(jù)科學借助統(tǒng)計學，這兩者不是一個概念。

同理，機器學習也并非人工智能；事實上，機器學習是人工智能的一個分支。這一點挺明顯的，因為我們基于以往的數(shù)據(jù)“教”（訓練）機器對特定類型的數(shù)據(jù)進行概括性的預測。

機器學習是基于統(tǒng)計學

在我們討論統(tǒng)計學和機器學習之間的區(qū)別前，我們先來說說其相似性，其實文章的前半段已經(jīng)對此有過一些探討了。

機器學習基于統(tǒng)計的框架，因為機器學習涉及數(shù)據(jù)，而數(shù)據(jù)必須基于統(tǒng)計學框架來進行描述，所以這點十分明顯。然而，擴展至針對大量粒子的熱力學的統(tǒng)計機制，同樣也建立在統(tǒng)計學框架之下。

壓力的概念其實是數(shù)據(jù)，溫度也是一種數(shù)據(jù)。你可能覺得這聽起來不合理，但這是真的。這就是為什么你不能描述一個分子的溫度或壓力，這不合理。溫度是分子相撞產(chǎn)生的平均能量的顯示。而例如房屋或室外這種擁有大量分子的，我們能用溫度來描述也就合理了。

你會認為熱力學和統(tǒng)計學是一個東西嗎？當然不會，熱力學借助統(tǒng)計學來幫助我們理解運動的相互作用以及轉移現(xiàn)象中產(chǎn)生的熱。

事實上，熱力學基于多種學科而非僅僅統(tǒng)計學。類似地，機器學習基于許多其他領域的內(nèi)容，比如數(shù)學和計算機科學。舉例來說：

機器學習的理論來源于數(shù)學和統(tǒng)計學

機器學習算法基于優(yōu)化理論、矩陣代數(shù)和微積分

機器學習的實現(xiàn)來源于計算機科學和工程學概念，比如核映射、特征散列等。

當一個人開始用Python開始編程，突然從Sklearn程序庫里找出并使用這些算法，許多上述的概念都比較抽象，因此很難看出其中的區(qū)別。這樣的情況下，這種抽象定義也就致使了對機器學習真正包含的內(nèi)容一定程度上的無知。

統(tǒng)計學習理論——機器學習的統(tǒng)計學基礎

統(tǒng)計學和機器學習之間最主要的區(qū)別在于統(tǒng)計學完全基于概率空間。你可以從集合論中推導出全部的統(tǒng)計學內(nèi)容，集合論討論了我們?nèi)绾螌?shù)據(jù)歸類（這些類被稱為“集”），然后對這個集進行某種測量保證其總和為1.我們將這種方法成為概率空間。

統(tǒng)計學除了對這些集合和測量有所定義之外沒有其他假設。這就是為什么我們對概率空間的定義非常嚴謹?shù)脑颉Ｒ粋€概率空間，其數(shù)學符號寫作(Ω,F,P)，包含三部分：

一個樣本空間，Ω，也就是所有可能結果的集合。

一個事件集合，F(xiàn)，每個事件都包含0或者其它值。

對每個事件發(fā)生的可能性賦予概率，P，這是一個從事件到概率的函數(shù)。

機器學習基于統(tǒng)計學習理論，統(tǒng)計學習理論也依舊基于對概率空間的公理化語言。這個理論基于傳統(tǒng)的統(tǒng)計學理論，并發(fā)展于19世紀60年代。

機器學習分為多個類別，這篇文章我僅著眼于監(jiān)督學習理論，因為它最容易解釋（雖然因其充斥數(shù)學概念依然顯得晦澀難懂）。

統(tǒng)計學習理論中的監(jiān)督學習，給了我們一個數(shù)據(jù)集，我們將其標為S= {(x?,y?)}，也就是說我們有一個包含N個數(shù)據(jù)點的數(shù)據(jù)集，每個數(shù)據(jù)點由被稱為“特征”的其它值描述，這些特征用x描述，這些特征通過特定函數(shù)來描繪以返回我們想要的y值。

已知這個數(shù)據(jù)集，問如何找到將x值映射到y(tǒng)值的函數(shù)。我們將所有可能的描述映射過程的函數(shù)集合稱為假設空間。

為了找到這個函數(shù)，我們需要給算法一些方法來“學習”如何最好地著手處理這個問題，而這由一個被稱為“損失函數(shù)”的概念來提供。因此，對我們所有的每個假設（也即提議的函數(shù)），我們要通過比較所有數(shù)據(jù)下其預期風險的值來衡量這個函數(shù)的表現(xiàn)。

預期風險本質(zhì)上就是損失函數(shù)之和乘以數(shù)據(jù)的概率分布。如果我們知道這個映射的聯(lián)合概率分布，找到最優(yōu)函數(shù)就很簡單了。但是這個聯(lián)合概率分布通常是未知的，因此我們最好的方式就是猜測一個最優(yōu)函數(shù)，再實證驗證損失函數(shù)是否得到優(yōu)化。我們將這種稱為實證風險。

之后，我們就可以比較不同函數(shù)，找出最小預期風險的那個假設，也就是所有函數(shù)中得出最小下確界值的那個假設。

然而，為了最小化損失函數(shù)，算法有通過過度擬合來作弊的傾向。這也是為什么要通過訓練集“學習”函數(shù)，之后在訓練集之外的數(shù)據(jù)集，測試集里對函數(shù)進行驗證。

我們?nèi)绾味x機器學習的本質(zhì)引出了過度擬合的問題，也對需要區(qū)分訓練集和測試集作出了解釋。而我們在統(tǒng)計學中無需試圖最小化實證風險，過度擬合不是統(tǒng)計學的固有特征。最小化統(tǒng)計學中無需視圖程向于一個從函數(shù)中選取最小化實證風險的學習算法被稱為實證風險最小化

例證

以線性回歸做一個簡單例子。在傳統(tǒng)概念中，我們試圖最小化數(shù)據(jù)中的誤差找到能夠描述數(shù)據(jù)的函數(shù)，這種情況下，我們通常使用均值方差。使用平方數(shù)是為了不讓正值和負值互相抵消。然后我們可以使用閉合表達式來求出回歸系數(shù)。

如果我們將損失函數(shù)計為均值方差，并基于統(tǒng)計學習理論進行最小化實證風險，碰巧就能得到傳統(tǒng)線性回歸分析同樣的結果。

這個巧合是因為兩個情況是相同的，對同樣的數(shù)據(jù)以相同的方式求解最大概率自然會得出相同的結果。最大化概率有不同的方法來實現(xiàn)同樣的目標，但沒人會去爭論說最大化概率與線性回歸是一個東西。這個最簡單的例子顯然沒能區(qū)分開這些方法。

這里要指出的第二點在于，傳統(tǒng)的統(tǒng)計方法中沒有訓練集和測試集的概念，但我們會使用不同的指標來幫助驗證模型。驗證過程雖然不同，但兩種方法都能夠給我們統(tǒng)計穩(wěn)健的結果。

另外要指出的一點在于，傳統(tǒng)統(tǒng)計方法給了我們一個閉合形式下的最優(yōu)解，它沒有對其它可能的函數(shù)進行測試來收斂出一個結果。相對的，機器學習方法嘗試了一批不同的模型，最后結合回歸算法的結果，收斂出一個最終的假設。

如果我們用一個不同的損失函數(shù)，結果可能并不收斂。例如，如果我們用了鉸鏈損失（使用標準梯度下降時不太好區(qū)分，因此需要使用類似近梯度下降等其它方法），那么結果就不會相同了。

最后可以對模型偏差進行區(qū)分。你可以用機器學習算法來測試線性模型以及多項式模型，指數(shù)模型等，來檢驗這些假設是否相對我們的先驗損失函數(shù)對數(shù)據(jù)集給出更好的擬合度。在傳統(tǒng)統(tǒng)計學概念中，我們選擇一個模型，評估其準確性，但無法自動從100個不同的模型中摘出最優(yōu)的那個。顯然，由于最開始選擇的算法不同，找出的模型總會存在一些偏誤。選擇算法是非常必要的，因為為數(shù)據(jù)集找出最優(yōu)的方程是一個NP-hard問題。

那么哪個方法更優(yōu)呢？

這個問題其實很蠢。沒有統(tǒng)計學，機器學習根本沒法存在，但由于當代信息爆炸人類能接觸到的大量數(shù)據(jù)，機器學習是非常有用的。

對比機器學習和統(tǒng)計模型還要更難一些，你需要視乎你的目標而定究竟選擇哪種。如果你只是想要創(chuàng)建一個高度準確的預測房價的算法，或者從數(shù)據(jù)中找出哪類人更容易得某種疾病，機器學習可能是更好的選擇。如果你希望找出變量之間的關系或從數(shù)據(jù)中得出推論，選擇統(tǒng)計模型會更好。

圖中文字：

這是你的機器學習系統(tǒng)？

對的，你從這頭把數(shù)據(jù)都倒進這一大堆或者線性代數(shù)里，然后從那頭里拿答案就好了。

答案錯了咋整？

那就攪攪，攪到看起來對了為止。

如果你統(tǒng)計學基礎不夠扎實，你依然可以學習機器學習并使用它——機器學習程序庫里的抽象概念能夠讓你以業(yè)余者的身份來輕松使用它們，但你還是得對統(tǒng)計概念有所了解，從而避免模型過度擬合或得出些貌似合理的推論。