如果你在新聞中看到有人成功制造出了量子計算機的話，你最好立刻凍結自己的信用卡。因為，當你在網上購物時，目前所有保護你的信用卡信息的方法將會在幾秒鐘內被量子計算機攻破。不光是你在銀行內的信息，所有的加密信息在量子計算機面前都將被輕松破解。

網絡安全依賴于一些很難解決的數學問題

關于量子計算機有很多聳人聽聞的說法，但是量子計算機破解加密信息的超強能力是真的。現有的加密方法是基于那些用普通計算機無法快速解決的數學問題設計的，但是量子計算機可以輕易攻破這種加密方法。那么量子計算機還有哪些明顯強于普通計算機的技能？

破譯密碼

雖然為了回答這個問題我們進行了很多理論方面的準備，但是這個問題仍舊很棘手。RSA算法，一種廣泛被用于保護信息安全的算法，它利用計算機都很難快速完成的因數分解來進行加密。如果給你一個數字10，你立刻就可以告訴我它可以被分解為2和5兩個素數的乘積，但是如果我給你的數字是62615533，你應該無法通過心算告訴我它是哪些素數的乘積。

這不能怪罪于你的心算能力。一旦數字足夠大，計算機也無能為力。“如果給出一個4000位的數字，即使是讓現存的計算機運行和宇宙年齡一樣長的時間也無法將它分解成一系列素數的乘積，”劍橋大學的量子計算先驅Richard Jozsa說。

其實還有其他很多問題和分解數字具有一樣的特征：我們有很多可以解決它們的算法，但是隨著要解決的問題的難度的增加，所需算法的步數也越多。另一個著名的問題是旅行商問題，這個問題是說如何讓旅行商訪問每個城市時所走的路程最短：要訪問的城市越多，問題越復雜。

復雜性理論按照解決問題的步數的增長速度來對各種問題進行分類。如果步數的增長是指數型的，比如旅行商問題，問題會變得非常棘手，因為指數型增長的增長速度會越來越快。當算法步數的增長隨著輸入數字的增加表現成多項式形式時，我們才認為這樣的問題是可解決的：如果輸入的大小是n，解題所需的步數正比于n2,n3或者nk。雖然解題步數增長在我們看來還是很快（假設k=10），但是復雜理論專家認為這種增長還算緩慢。“步數增長表現為多項式的數學模型是可計算的，”Jozsa解釋道，“如果步數增長不表現為多項式的形式，我們認為這類問題在實際操作中是無法解決的。”

因數分解被認為是不可解決的問題：沒有人寫出可以由我們現在的計算機運行的多項式時間（步數呈多項式型增長）算法。這正是量子計算可以大展神威之處。1994年數學家Peter Shor提出一種解決數字分解問題的量子算法，它不光是多項式時間算法，并且k不大于3。這個算法利用數論的知識，將因數分解問題轉化成一種在特定的數學函數中識別周期模式的問題——模式識別正是量子計算機所擅長的。

如今使用的其他加密算法也存在類似的問題，例如橢圓曲線加密算法（elliptic curve cryptography）：量子計算機可以輕易破解它們。

這看起來量子計算機有很大優勢，但在這個領域內任何事情都是不確定的。“在復雜性理論中，要證明給定的任務不能在多項式時間內解決是出了名的難題，”Jozsa說，“這是一個尷尬的事實。”因為沒人知道因數分解的多項式時間算法，并不意味著這樣一個等待我們發現的算法不存在。“也許，下周可能就有一個聰明的數論專家把這樣的算法找出來，” Jozsa說，“對量子計算來說，這有點掃興。”

復雜性問題

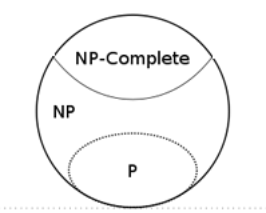
復雜性的等級

對于其他問題情況怎么樣？在其他的比因數分解更難的問題中，量子計算的威力會超過經典計算嗎？在回答這個問題之前我們要明確“更難”的含義，這把我們引導到了復雜性類（complexity classes）的分級這里。首先介紹“簡單的”問題，這類問題擁有可在經典計算機上運行的多項式時間算法，這類問題組成了一個被稱為P的類。接下來是我們沒有找到多項式時間算法的問題，但我們可以在多項式時間內來檢驗解的正確性。這類問題被稱為NP問題。因數分解正是屬于這類問題。

在NP類問題中，有一些問題特別難解——這些問題被稱為NP完全問題（NP-complete），旅行商問題屬于這類問題。比NP完全問題更加復雜的問題這里將不再介紹。

因數分解被歸納于NP類問題但不屬于NP完全問題。由于量子計算可以在因數分解問題中擊敗經典計算，接下來的問題是，當涉及NP完全問題時，量子計算機表現如何？有一種說法認為，量子計算機可以在眨眼之間解決NP完全問題。但這種說法過于樂觀了。“我們不知道我們是否可以用量子計算機解決NP完全問題，事實上，我們認為量子計算機做不到這一點，”Jozsa解釋道。

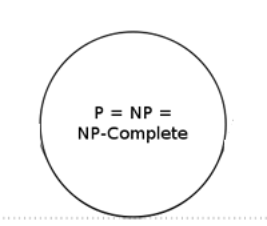
P和NP問題是同樣復雜的問題嗎？

在這里，我們應該認識到復雜性理論的核心問題：所有我們提到的東西都不能被證明。我們不僅不知道量子計算機能否有效地解決NP完全問題，甚至不知道普通計算機能否有效地解決這些問題。正如可能存在一個可以解決因數分解問題但尚未被發現的多項式時間算法一樣，也可能存在解決其他NP問題或NP完全問題的多項式時間算法。如果我們找到了這些算法，那么我們的復雜性類層次的結構將會崩潰：P類、NP類和NP完全類將會屬于同一類。如果你能證明或否定P類問題等價于NP類問題，那就厲害了，克萊數學研究所都會獎勵你一百萬美元：它被認為是數學中最有趣的七個開放問題之一。

量子計算機會做什么?

如果理論不是建立在堅實的基礎上,那么我們怎樣保證量子計算可以有實際用處呢？P問題在理論上是“容易”解決的，但是你仍然需要花費很多時間去解決它。這時量子計算機可以幫助我們嗎？

答案是肯定的。一個例子是“大海撈針”問題，它指的是從龐大無規律的數據庫中找到特定的信息。試想，從包含n個條目的電話號碼簿中搜索一個特定的號碼而不是一個特定的名字。這是一個需要消耗大量時間的任務，因為號碼是無規則的，它不像名字一樣是按規律排列的。經典計算機除了一個一個的檢索號碼之外沒有其他辦法，最壞的情況是，我們發現電話號碼簿中根本不存在我們要找的號碼，或者這個號碼處于最后一個位置，這樣就需要進行n次操作。而量子計算機只需要n0.5次操作。這看起來并沒有提速多少，但是當n足夠大時，提速是相當可觀的：以n=1000000為例，經典計算機需要進行一百萬次操作而量子計算機僅需要進行1000次操作。

分子由大量遵循量子規律的粒子組成

另一個量子計算機可以大展身手的領域是化學領域，生物和制藥領域。如果你想理解一個分子系統，例如為了設計一種新藥，一個明智的選擇就是在計算機上模擬它的行為。困難在于分子是由很多粒子組成的，而這些粒子全部遵循量子力學的規律。我們知道，隨著粒子數的增長，描述分子系統所需的信息量呈指數增長，這使得計算變得異常困難。“它具有指數級的復雜性，”Jozas說，“盡管是面對相對小的分子，最好的經典計算機在模擬分子的量子動力學性質時也顯得無能為力，然而量子計算機可以勝任這項工作。”

密碼學也會受益于量子計算機。例如，當量子態被觀測時就會發生塌縮，利用這種性質可以監測信息是否被其他人竊取。利用這種方法，人們可以給每個人分發量子秘鑰——一串可以用于對信息加密和解密的字符串。如果有人截獲了秘鑰我們馬上就能知道。“這種器件之所以存在，是因為它們只需要幾個量子比特，因此這屬于量子技術的范疇。”Jozsa說。這種方法在2007年首次被用于公共實踐，當時它被用來確保在瑞士日內瓦舉行的選舉中的選票安全轉移。也許從理論的角度我們很難說量子計算機具有什么優勢，但是至少我們知道破壞我們的加密方法是要付出一些代價的。