1. 線性回歸

在統計學和機器學習領域，線性回歸可能是最廣為人知也最易理解的算法之一。

預測建模主要關注的是在犧牲可解釋性的情況下，盡可能最小化模型誤差或做出最準確的預測。我們將借鑒、重用來自許多其它領域的算法（包括統計學）來實現這些目標。

線性回歸模型被表示為一個方程式，它為輸入變量找到特定的權重（即系數 B），進而描述一條最佳擬合了輸入變量（x）和輸出變量（y）之間關系的直線。

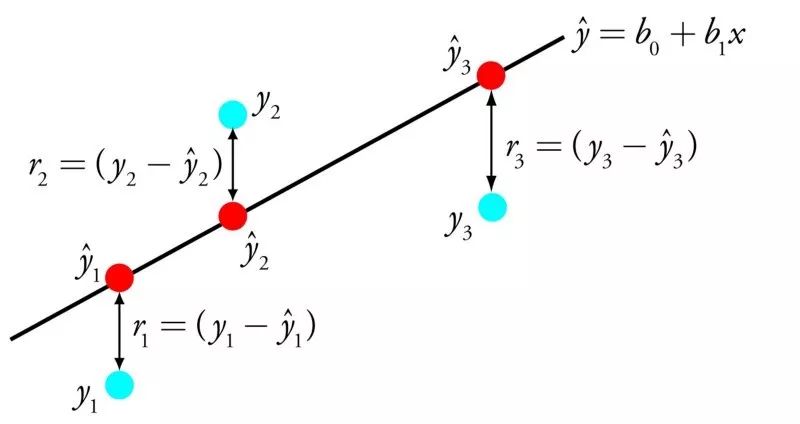
線性回歸

例如： y = B0 + B1 * x

我們將在給定輸入值 x 的條件下預測 y，線性回歸學習算法的目的是找到系數 B0 和 B1 的值。

我們可以使用不同的技術來從數據中學習線性回歸模型，例如普通最小二乘法的線性代數解和梯度下降優化。

線性回歸大約有 200 多年的歷史，并已被廣泛地研究。在使用此類技術時，有一些很好的經驗規則：我們可以刪除非常類似（相關）的變量，并盡可能移除數據中的噪聲。線性回歸是一種運算速度很快的簡單技術，也是一種適合初學者嘗試的經典算法。

2. Logistic 回歸

Logistic 回歸是機器學習從統計學領域借鑒過來的另一種技術。它是二分類問題的首選方法。

像線性回歸一樣，Logistic 回歸的目的也是找到每個輸入變量的權重系數值。但不同的是，Logistic 回歸的輸出預測結果是通過一個叫作「logistic 函數」的非線性函數變換而來的。

logistic 函數的形狀看起來像一個大的「S」，它會把任何值轉換至 0-1 的區間內。這十分有用，因為我們可以把一個規則應用于 logistic 函數的輸出，從而得到 0-1 區間內的捕捉值（例如，將閾值設置為 0.5，則如果函數值小于 0.5，則輸出值為 1），并預測類別的值。

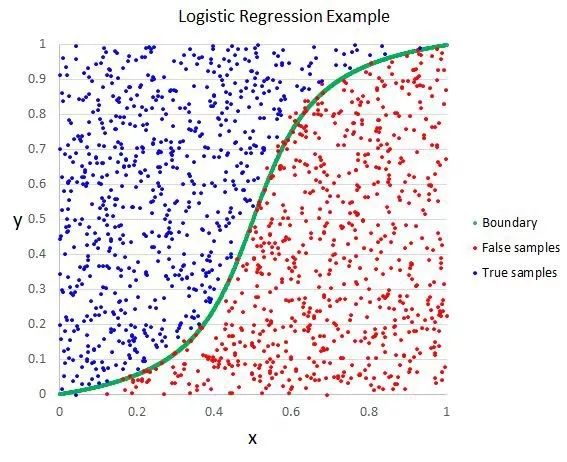
Logistic 回歸

由于模型的學習方式，Logistic 回歸的預測結果也可以用作給定數據實例屬于類 0 或類 1 的概率。這對于需要為預測結果提供更多理論依據的問題非常有用。

與線性回歸類似，當刪除與輸出變量無關以及彼此之間非常相似（相關）的屬性后，Logistic 回歸的效果更好。該模型學習速度快，對二分類問題十分有效。

3. 線性判別分析

Logistic 回歸是一種傳統的分類算法，它的使用場景僅限于二分類問題。如果你有兩個以上的類，那么線性判別分析算法（LDA）是首選的線性分類技術。

LDA 的表示方法非常直接。它包含為每個類計算的數據統計屬性。對于單個輸入變量而言，這些屬性包括：

每個類的均值。

所有類的方差。

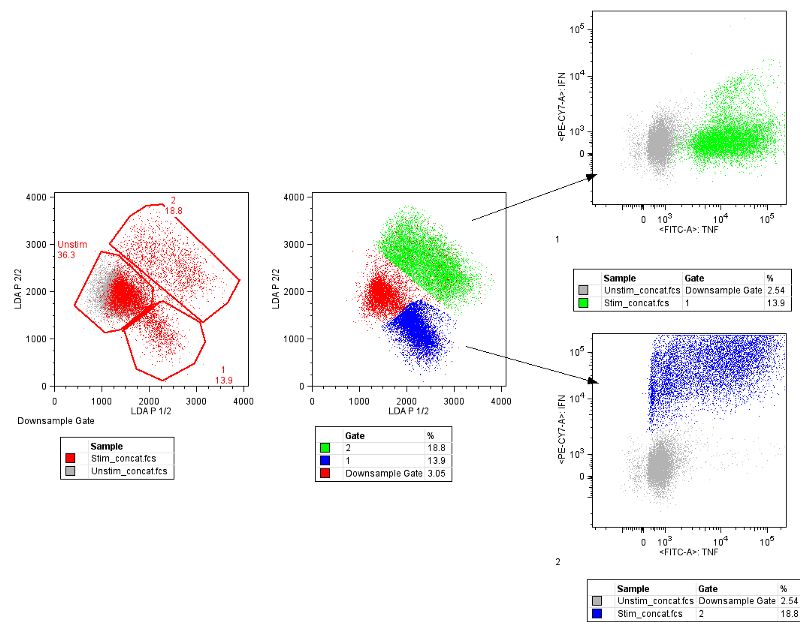
線性判別分析

預測結果是通過計算每個類的判別值、并將類別預測為判別值最大的類而得出的。該技術假設數據符合高斯分布（鐘形曲線），因此最好預先從數據中刪除異常值。LDA 是一種簡單而有效的分類預測建模方法。

4. 分類和回歸樹

決策樹是一類重要的機器學習預測建模算法。

決策樹可以被表示為一棵二叉樹。這種二叉樹與算法設計和數據結構中的二叉樹是一樣的，沒有什么特別。每個節點都代表一個輸入變量（x）和一個基于該變量的分叉點（假設該變量是數值型的）。

決策樹

決策樹的葉子結點包含一個用于做出預測的輸出變量（y）。預測結果是通過在樹的各個分叉路徑上游走，直到到達一個葉子結點并輸出該葉子結點的類別值而得出。

決策樹的學習速度很快，做出預測的速度也很快。它們在大量問題中往往都很準確，而且不需要為數據做任何特殊的預處理準備。

5. 樸素貝葉斯

樸素貝葉斯是一種簡單而強大的預測建模算法。

該模型由兩類可直接從訓練數據中計算出來的概率組成：1）數據屬于每一類的概率；2）給定每個 x 值，數據從屬于每個類的條件概率。一旦這兩個概率被計算出來，就可以使用貝葉斯定理，用概率模型對新數據進行預測。當你的數據是實值的時候，通常假設數據符合高斯分布（鐘形曲線），這樣你就可以很容易地估計這些概率。

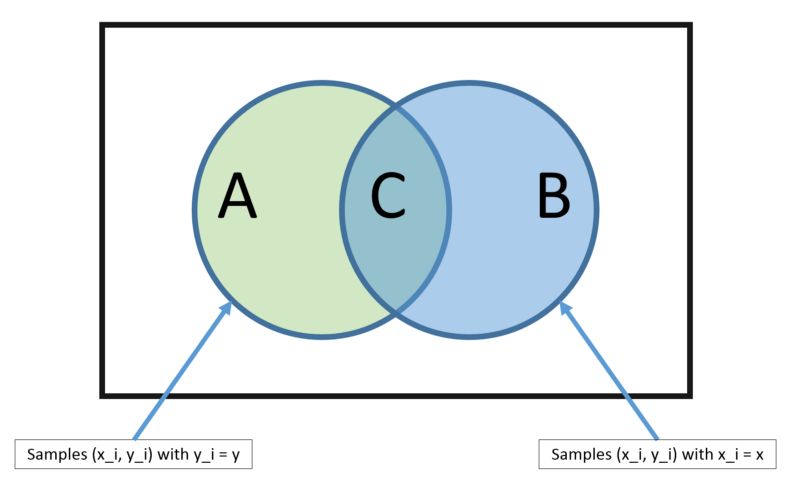
貝葉斯定理

樸素貝葉斯之所以被稱為「樸素」，是因為它假設每個輸入變量相互之間是獨立的。這是一種很強的、對于真實數據并不現實的假設。不過，該算法在大量的復雜問題中十分有效。

6. K 最近鄰算法

K 最近鄰（KNN）算法是非常簡單而有效的。KNN 的模型表示就是整個訓練數據集。這很簡單吧？

對新數據點的預測結果是通過在整個訓練集上搜索與該數據點最相似的 K 個實例（近鄰）并且總結這 K 個實例的輸出變量而得出的。對于回歸問題來說，預測結果可能就是輸出變量的均值；而對于分類問題來說，預測結果可能是眾數（或最常見的）的類的值。

關鍵之處在于如何判定數據實例之間的相似程度。如果你的數據特征尺度相同（例如，都以英寸為單位），那么最簡單的度量技術就是使用歐幾里得距離，你可以根據輸入變量之間的差異直接計算出該值。

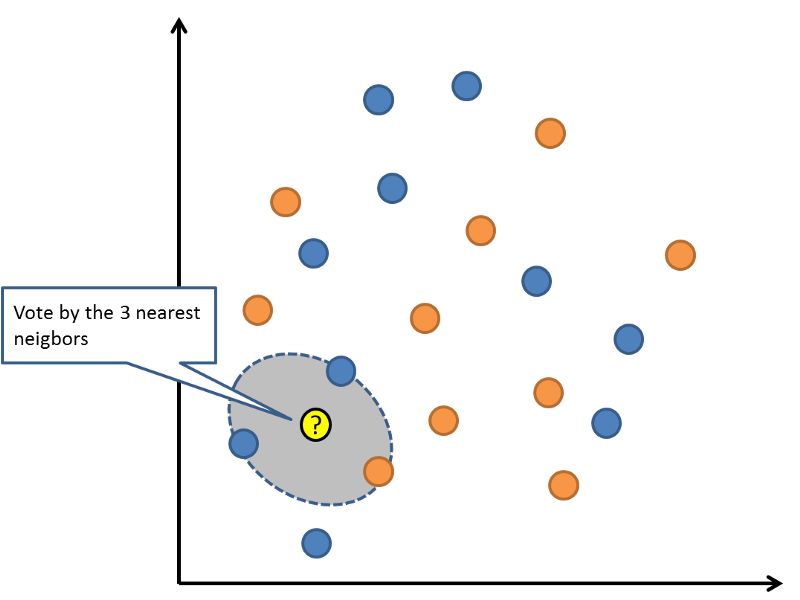
K 最近鄰

KNN 可能需要大量的內存或空間來存儲所有數據，但只有在需要預測時才實時執行計算（或學習）。隨著時間的推移，你還可以更新并管理訓練實例，以保證預測的準確率。

使用距離或接近程度的度量方法可能會在維度非常高的情況下（有許多輸入變量）崩潰，這可能會對算法在你的問題上的性能產生負面影響。這就是所謂的維數災難。這告訴我們，應該僅僅使用那些與預測輸出變量最相關的輸入變量。

7. 學習向量量化

KNN 算法的一個缺點是，你需要處理整個訓練數據集。而學習向量量化算法（LVQ）允許選擇所需訓練實例數量，并確切地學習這些實例。

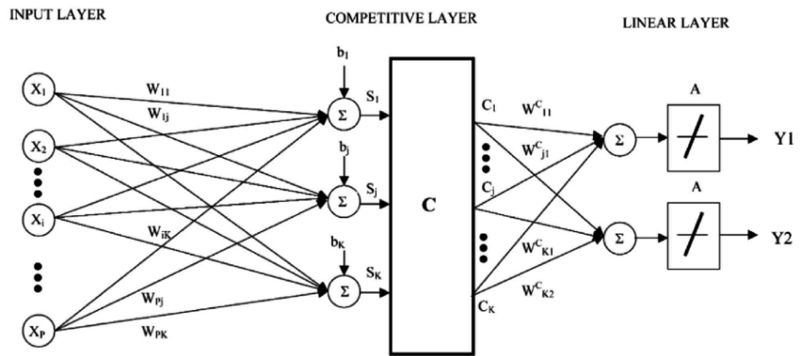
學習向量量化

LVQ 的表示是一組碼本向量。它們在開始時是隨機選擇的，經過多輪學習算法的迭代后，最終對訓練數據集進行最好的總結。通過學習，碼本向量可被用來像 K 最近鄰那樣執行預測。通過計算每個碼本向量與新數據實例之間的距離，可以找到最相似的鄰居（最匹配的碼本向量）。然后返回最匹配單元的類別值（分類）或實值（回歸）作為預測結果。如果將數據重新放縮放到相同的范圍中（例如 0 到 1 之間），就可以獲得最佳的預測結果。

如果你發現 KNN 能夠在你的數據集上得到不錯的預測結果，那么不妨試一試 LVQ 技術，它可以減少對內存空間的需求，不需要像 KNN 那樣存儲整個訓練數據集。

8. 支持向量機

支持向量機（SVM）可能是目前最流行、被討論地最多的機器學習算法之一。

超平面是一條對輸入變量空間進行劃分的「直線」。支持向量機會選出一個將輸入變量空間中的點按類（類 0 或類 1）進行最佳分割的超平面。在二維空間中，你可以把他想象成一條直線，假設所有輸入點都可以被這條直線完全地劃分開來。SVM 學習算法旨在尋找最終通過超平面得到最佳類別分割的系數。

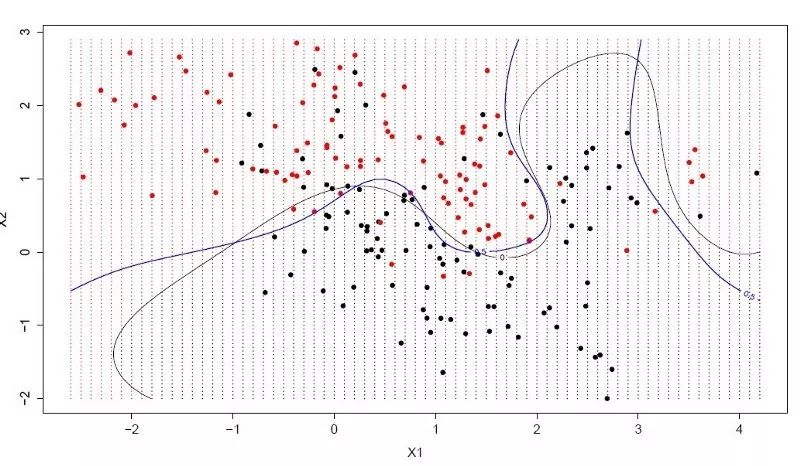
支持向量機

超平面與最近數據點之間的距離叫作間隔（margin）。能夠將兩個類分開的最佳超平面是具有最大間隔的直線。只有這些點與超平面的定義和分類器的構建有關，這些點叫作支持向量，它們支持或定義超平面。在實際應用中，人們采用一種優化算法來尋找使間隔最大化的系數值。

支持向量機可能是目前可以直接使用的最強大的分類器之一，值得你在自己的數據集上試一試。

9. 袋裝法和隨機森林

隨機森林是最流行也最強大的機器學習算法之一，它是一種集成機器學習算法。

自助法是一種從數據樣本中估計某個量（例如平均值）的強大統計學方法。你需要在數據中取出大量的樣本，計算均值，然后對每次取樣計算出的均值再取平均，從而得到對所有數據的真實均值更好的估計。

Bagging 使用了相同的方法。但是最常見的做法是使用決策樹，而不是對整個統計模型進行估計。Bagging 會在訓練數據中取多個樣本，然后為每個數據樣本構建模型。當你需要對新數據進行預測時，每個模型都會產生一個預測結果，Bagging 會對所有模型的預測結果取平均，以便更好地估計真實的輸出值。

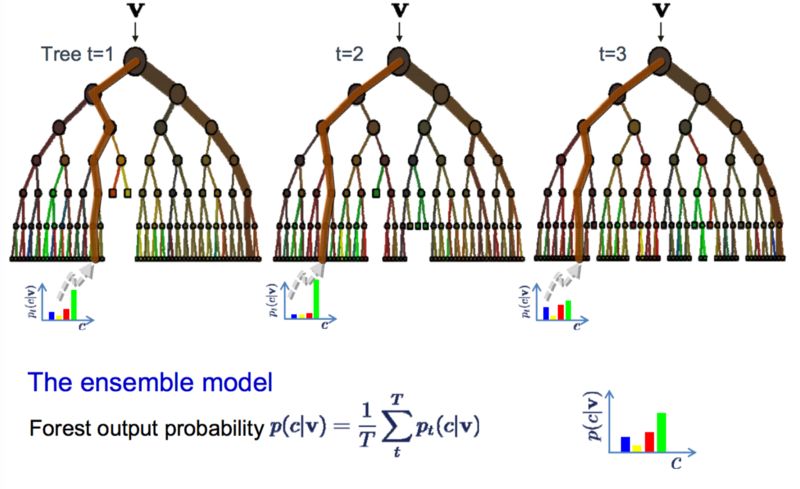
隨機森林

隨機森林是這種方法的改進，它會創建決策樹，這樣就不用選擇最優分割點，而是通過引入隨機性來進行次優分割。

因此，為每個數據樣本創建的模型比在其它情況下創建的模型更加獨特，但是這種獨特的方式仍能保證較高的準確率。結合它們的預測結果可以更好地估計真實的輸出值。

如果你使用具有高方差的算法（例如決策樹）獲得了良好的結果，那么你通常可以通過對該算法執行 Bagging 獲得更好的結果。

10. Boosting 和 AdaBoost

Boosting 是一種試圖利用大量弱分類器創建一個強分類器的集成技術。要實現 Boosting 方法，首先你需要利用訓練數據構建一個模型，然后創建第二個模型（它企圖修正第一個模型的誤差）。直到最后模型能夠對訓練集進行完美地預測或加入的模型數量已達上限，我們才停止加入新的模型。

AdaBoost 是第一個為二分類問題開發的真正成功的 Boosting 算法。它是人們入門理解 Boosting 的最佳起點。當下的 Boosting 方法建立在 AdaBoost 基礎之上，最著名的就是隨機梯度提升機。

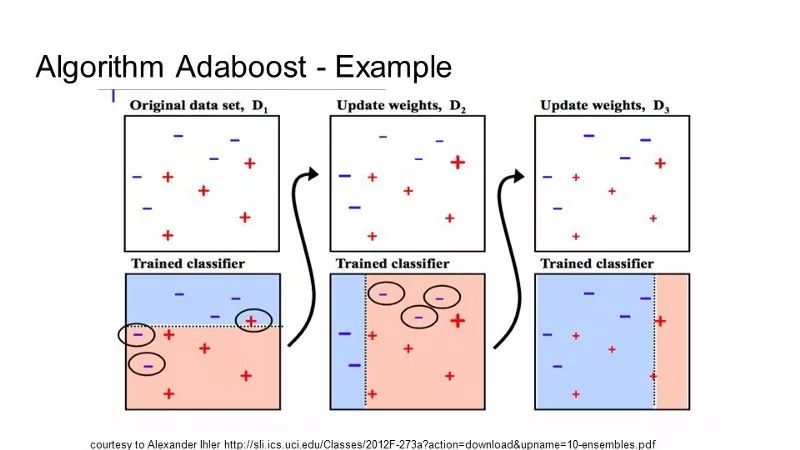
AdaBoost

AdaBoost 使用淺層決策樹。在創建第一棵樹之后，使用該樹在每個訓練實例上的性能來衡量下一棵樹應該對每個訓練實例賦予多少權重。難以預測的訓練數據權重會增大，而易于預測的實例權重會減小。模型是一個接一個依次創建的，每個模型都會更新訓練實例權重，影響序列中下一棵樹的學習。在構建所有的樹之后，我們就可以對新的數據執行預測，并根據每棵樹在訓練數據上的準確率來對其性能進行加權。