電感器和扼流圈基本上是繞在線圈上的線圈或線圈空心管形成器(空心芯)或繞一些鐵磁材料(鐵芯)纏繞以增加其感應值,稱為電感。
電感器以磁場的形式存儲它們的能量當在電感器的端子上施加電壓時產生。流過電感器的電流的增長不是瞬時的,而是由電感器自身的自感應或反電動勢值決定的。然后對于電感線圈,該反電動勢電壓V L 與流過它的電流的變化率成比例。
此電流將繼續上升,直到達到其最大穩態狀態,這個時間約為五個時間常數,此時這個自感應反電動勢已經衰減到零。此時穩態電流流過線圈,不再產生反電動勢來阻止電流流動,因此,線圈更像是一個短路,允許最大電流流過它。
然而,在包含AC電感的交流電路中,通過電感器的電流的行為與穩態DC電壓的行為非常不同。現在在交流電路中,流過線圈繞組的電流的反對不僅取決于線圈的電感,還取決于施加電壓波形的頻率,因為它從正值變為負值。
流過AC電路中的線圈的電流的實際反對由線圈的AC電阻確定,該AC電阻由復數表示。但是為了區分直流電阻值和交流電阻值(也稱為阻抗),使用術語電抗。
類似電阻,電抗以歐姆為單位測量,但是給出符號“X”以區別于純電阻“R”值,并且由于所討論的元件是電感器,電感器的電抗稱為感應電抗,( X L )并以歐姆為單位測量。其值可以從公式中找到。
感應電抗

其中: X L 是以歐姆為單位的感應電抗,?是以赫茲為單位的頻率, L 是亨利斯中線圈的電感。
我們還可以用弧度定義感抗,其中歐米茄,ω等于2π。
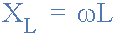
因此,無論何時向電感線圈施加正弦電壓,反電動勢都會反對流過線圈的電流的上升和下降以及純電感線圈,該電感線圈具有零電阻或損耗,這種阻抗(可以是一個復數)等于它的歸納電抗。電抗也表示電抗,因為它具有幅度和方向(角度)。考慮下面的電路。
具有正弦電源的交流電感
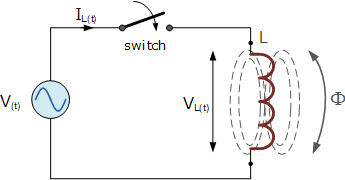
上述簡單電路由 L Henries( H ),連接在由表達式給出的正弦電壓上: V(t)= V max sinωt 。當開關閉合時,該正弦電壓將使電流流動并從零上升到其最大值。電流的這種上升或變化將在線圈內產生磁場,這反過來將阻止或限制電流的這種變化。
但是在電流有時間達到其最大值之前在直流電路中,電壓改變極性,導致電流改變方向。另一方向的這種變化再次被線圈中的自感應反電動勢延遲,并且在僅包含純電感的電路中,電流延遲了90 o 。
施加的電壓在電流達到其最大正值之前的一個周期的四分之一( 1 /4?)達到其最大正值,換句話說,施加到純電感電路的電壓“引導”電流四分之一周期或90 o ,如下所示。
交流電感的正弦波形

這種效應也可以用相量圖表示,在純電感電路中,電壓“LEADS”電流為90 o 。但是通過使用電壓作為參考,我們也可以說電流“LAGS”電壓是一個周期的四分之一或90 o ,如下面的矢量圖所示。
交流電感的相量圖
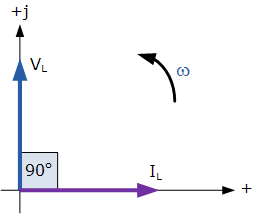
因此,對于純損耗電感, V L “引導” I L 90 o ,或者我們可以說 I L “滯后” V L 90 o 。
有許多不同的方法來記住流過純電感電路的電壓和電流之間的相位關系,但一種非常簡單易記的方法是使用助記符表達式“ELI”(發音為艾莉在女孩的名字中)。 ELI 首先表示在電流 I 之前的交流電感 L 中的 E 電動勢。換句話說,電感器中電流之前的電壓 E , L , I 等于“ELI”,無論電壓從哪個相角開始,這個表達式總是適用于純電感電路。
頻率對感應電抗的影響
當50Hz電源連接到合適的交流電感時,電流將如前所述延遲90 o 并將獲得在每個半周期結束時電壓反轉極性之前的峰值 I 安培,即電流在“ T secs ”中上升到其最大值。
如果我們現在向線圈施加相同峰值電壓的100Hz電源,電流仍將延遲90 o ,但其最大值將低于50Hz值,因為由于頻率的增加,它需要達到其最大值所需的時間已減少,因為現在它只有“ 1/2 T secs ”才能達到其峰值。此外,由于頻率的增加,線圈內磁通量的變化率也增加。
然后從上面的感抗電抗方程中可以看出,如果頻率或者電感增加,線圈的總感應電抗值也會增加。隨著頻率增加并接近無窮大,電感器電抗,因此它的阻抗也會朝向無窮大增加,就像開路一樣。
同樣,當頻率接近零或DC時,電感器電抗也會減小到零,表現得像一個短路。這意味著感應電抗“與頻率成正比”并且在低頻時具有較小值,在較高頻率時具有較高值,如圖所示。
對頻率的感應電抗

電感的感抗隨著其上的頻率增加而增加,因此感抗與頻率成正比( X L α?)因為電感中產生的反電動勢等于其電感乘以電感中電流的變化率。
隨著頻率的增加,流過電感的電流也會減小。
我們可以將非常低和非常高的頻率對純交流電感的電抗的影響表示如下:
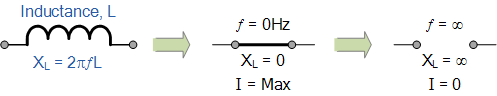
在包含純電感的交流電路中,適用以下公式:

<那么我們是如何得出這個等式的呢?因此,電感中的自感電動勢由法拉第定律確定,該法則由于電流的變化率而在電感器中產生自感應效應,并且感應電動勢的最大值將對應于最大變化率。然后電感線圈中的電壓如下:

然后將定義交流電感兩端的電壓as:
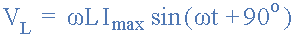
其中: V L =IωL這是電壓幅度和θ= + 90 o ,它是電壓和電流之間的相位差或相角。
在相量域中
在相量域中,線圈兩端的電壓如下:

在極地形式中,這將寫為: X L ∠90 o 其中:
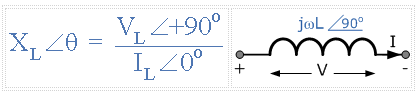

AC通過R + L系列電路
我們在上面已經看到流經純電感線圈的電流滯后電壓 90 o 當我們說純電感線圈時,我們指的是沒有歐姆電阻的線圈,因此,沒有 I 2 R 損失。但在現實世界中,不可能只有純粹的AC電感。
所有電氣線圈,繼電器,螺線管和變壓器都將具有一定的電阻,無論使用的線圈匝數有多小。這是因為銅線具有電阻率。然后我們可以認為我們的感應線圈是一個電阻, R 串聯一個電感, L 產生的東西可以被稱為“不純電感”。 / p>
如果線圈有一些“內部”電阻,那么我們需要將線圈的總阻抗表示為與電感串聯的電阻,并且在包含兩個電感的交流電路中, L 和電阻, R 組合電壓 V 將是兩個分量電壓的相量和, V R 和 V L 。
這意味著流過線圈的電流仍然會滯后于電壓,但是會少一些超過90 o 取決于 V R 和 V L 的值,相量和。電壓波形和電流波形之間的新角度給出了它們的相位差,正如我們所知,給定希臘符號phi,Φ的電路的相位角。
考慮到下面的電路是純無感電阻, R 與純電感串聯連接, L 。
串聯電阻電感電路
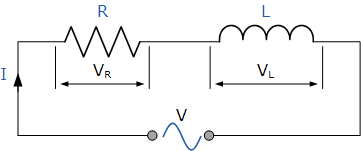
在上面的RL系列電路中,我們可以看到電流對電阻和電感都是常見的電壓由兩個分量電壓組成, V R 和 V L 。可以通過數學方法或通過繪制矢量圖找到這兩個分量的最終電壓。為了能夠產生矢量圖,必須找到參考或公共元件,并且在串聯AC電路中,當相同的電流流過電阻和電感時,電流是參考源。純電阻和純電感的單獨矢量圖如下:
兩個純元件的矢量圖
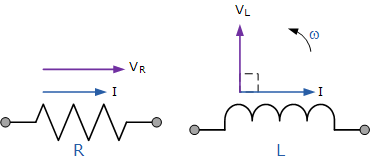
我們可以從上面和我們之前關于交流電阻的教程中看到,電阻電路中的電壓和電流都是同相的,因此矢量 V R 被繪制疊加以縮放到當前矢量上。同樣從上面可知,電流滯后于交流電感(純)電路中的電壓,因此矢量 V L 被繪制為90 o in電流的前面和與 V R 相同的比例,如圖所示。
結果電壓的矢量圖

從上面的矢量圖中,我們可以看到 OB 行是水平電流參考,行 OA 是電阻元件兩端的電壓,與電流同相。線 OC 表示電流前的感應電壓為90 o ,因此仍然可以看出電流滯后于純感應電壓90 o 。線 OD 給出了產生的電源電壓。然后:
V 等于所施加電壓的r.m.s值。
I 等于r.m.s.串聯電流的值。
V R 等于電阻上的 IR 電壓降,與電壓同相電流。
V L 等于電感上的 IX L 電壓降電流超過90 o 。
由于電流將純電感中的電壓精確地滯后90° o 得到的相量圖從各個電壓降中得出 V R 和 V L 表示上面顯示為 OAD 。然后我們也可以使用畢達哥拉斯定理在數學上找到電阻/電感(RL)電路上的合成電壓值。
As V R = IR 和 V L = IX L 施加的電壓將是兩者的矢量和,如下所示:

數量  代表阻抗,電路的 Z 。
代表阻抗,電路的 Z 。
交流電感的阻抗
阻抗,Z是對電流的“全面”反對在包含電阻,(實部)和電抗(虛部)的交流電路中流動。阻抗也具有歐姆單位,Ω。阻抗取決于電路的頻率,ω,因為這會影響電路無功元件,而在串聯電路中,所有電阻和無功阻抗都會加在一起。
阻抗也可以表示通過復數, Z = R + jX L 但它不是相量,它是兩個或多個相量組合在一起的結果。如果我們將電壓三角形的兩側除以 I ,則得到另一個三角形,其邊代表電路的電阻,電抗和阻抗,如下所示。
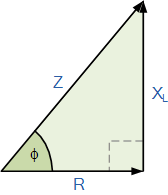
RL阻抗三角形

然后:<跨度>(阻抗) 2 =(抵抗) 2 +( j Reactance) 2 其中 j 代表90 o 相移。
這意味著電壓和電流之間的正相角θ給出為。
相角
雖然我們上面的示例代表一個簡單的非純交流電感,但如果兩個或多個感應線圈串聯在一起或者一個線圈與許多非感應電阻串聯,那么電阻元件的總電阻將等于: R 1 + R 2 + R 3 等,給出電路的總電阻值。
同樣,電感元件的總電抗等于: X 1 + X 2 + X 3 等,給出總電抗電路的價值。這樣,包含許多扼流圈,線圈和電阻的電路可以很容易地降低到阻抗值, Z 包括與單個電抗串聯的單個電阻, Z 2 =R2+X2.
AC電感示例No1
在以下電路中,電源電壓定義為: V (t) = 230 sin(314t - 30 o )且 L = 2.2H 。確定流過線圈的電流值并繪制得到的相量圖。
電壓兩端的電壓線圈將與電源電壓相同。將此時域值轉換為極坐標形式可以得到: V L = 230∠-30 o (v)。線圈的感抗是: X L =ωL= 314×2.2 =690Ω。然后流過線圈的電流可以使用歐姆定律找到:

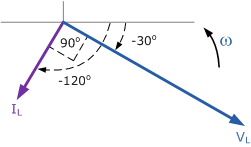
電流滯后電壓通過90 o 相量圖將是。

AC電感實例No2
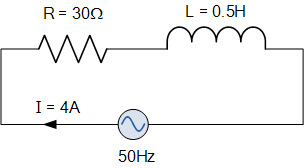
A線圈的電阻為30Ω,電感為0.5H。如果流過線圈的電流是4安培。如果頻率為50Hz,電源電壓的值是多少。

電路的阻抗將是be:
然后,每個組件的電壓降計算如下:
電流和電源電壓之間的相角計算如下:
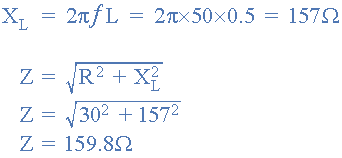
相量圖將是。

在下一篇關于交流電容的教程,我們將看一下電容器的穩壓狀態正弦交流波形的電壓 - 電流關系,以及純電容器和非純電容器的相量圖表示。
-
電感器
+關注
關注
20文章
2325瀏覽量
70420 -
頻率
+關注
關注
4文章
1459瀏覽量
59161 -
電抗
+關注
關注
1文章
24瀏覽量
21467
發布評論請先 登錄
相關推薦
電路小知識 | 交流電路復數的基礎知識以及相位差和電抗的計算
【電路小知識】交流電路基礎知識和波形的種類
電感器有哪些主要功能
交流發電機整流器怎樣將交流電變成直流電
交流電源模塊測試方法:如何測試電源頻率
如何保證交流電抗器的性能呢?
電抗器的作用及原理 電抗器好壞怎么測量
解析功率電感器的嘯叫原因及有效對策




 不同交流電感器和電抗頻率案例
不同交流電感器和電抗頻率案例










評論