Phasor Diagrams是表示兩個(gè)或多個(gè)交替量之間的幅度和方向關(guān)系的圖形方式
相同頻率的正弦波形之間可能存在相位差,表示角度差兩個(gè)正弦波形。此外,術(shù)語“引導(dǎo)”和“滯后”以及“同相”和“異相”通常用于表示一個(gè)波形與另一個(gè)波形的關(guān)系,其中廣義正弦表達(dá)式如下: (t) = A m sin(ωt±Φ)表示時(shí)域形式的正弦曲線。
但是當(dāng)以這種方式以數(shù)學(xué)方式呈現(xiàn),有時(shí)難以可視化兩個(gè)或更多個(gè)正弦波形之間的這種角度或相量差異。克服這個(gè)問題的一種方法是使用Phasor Diagrams以空間或相量域形式在圖形上表示正弦曲線,這是通過旋轉(zhuǎn)矢量法實(shí)現(xiàn)的。
基本上旋轉(zhuǎn)矢量,簡稱為“相量”是一個(gè)縮放線,其長度表示一個(gè)具有幅度(“峰值幅度”)和方向(“相位”)的交流量,它在“凍結(jié)”時(shí)某個(gè)時(shí)間點(diǎn)。
相量是一個(gè)在一端有箭頭的矢量,它部分表示矢量的最大值( V 或 I )部分是旋轉(zhuǎn)矢量的結(jié)束。
通常,假設(shè)矢量在一端圍繞一個(gè)稱為“原點(diǎn)”的固定零點(diǎn)旋轉(zhuǎn),而箭頭表示數(shù)量,在每個(gè)循環(huán)的一個(gè)完整旋轉(zhuǎn)的角速度(ω)下沿逆時(shí)針方向方向自由旋轉(zhuǎn)。矢量的這種逆時(shí)針旋轉(zhuǎn)被認(rèn)為是正旋轉(zhuǎn)。同樣,順時(shí)針旋轉(zhuǎn)被認(rèn)為是負(fù)旋轉(zhuǎn)。
雖然術(shù)語矢量和相量都用于描述旋轉(zhuǎn)線本身具有幅度和方向,但兩者之間的主要區(qū)別是矢量幅度是正弦波的“峰值”,而相量幅度是正弦波的“rms值”。在這兩種情況下,相位角和方向保持不變。
任何時(shí)刻交替量的相位都可以用相量圖表示,因此相量圖可以被認(rèn)為是“時(shí)間函數(shù)” ”。可以通過以ω=2π的角速度旋轉(zhuǎn)的單個(gè)矢量來構(gòu)造完整的正弦波,其中 f 是波形的頻率。然后Phasor是一個(gè)同時(shí)具有“幅度”和“方向”的數(shù)量。
通常,在構(gòu)建相量圖時(shí),總是假設(shè)正弦波的角速度為:ω,單位為rad / sec。考慮下面的相量圖。
正弦波形的相量圖

作為單向量以逆時(shí)針方向旋轉(zhuǎn),其尖端 A 將旋轉(zhuǎn)一整圈 360 o 或2π代表一個(gè)完整的循環(huán)。如果其移動(dòng)尖端的長度以不同的角度間隔在時(shí)間上傳遞到如上所示的曲線圖,則將在零時(shí)間從左側(cè)開始繪制正弦波形。沿水平軸的每個(gè)位置表示從零時(shí)間開始經(jīng)過的時(shí)間, t = 0 。當(dāng)向量是水平的時(shí),向量的尖端代表0 o ,180 o 和360 o 的角度。
同樣,當(dāng)矢量的尖端是垂直的時(shí),它代表90 o 或π/ 2 + Am ) >和負(fù)峰值,( -Am )在270 o 或3π/ 2 。然后,波形的時(shí)間軸表示相量移動(dòng)的角度或弧度。因此我們可以說相量代表旋轉(zhuǎn)矢量的縮放電壓或電流值,它在某個(gè)時(shí)間點(diǎn)“凍結(jié)”( t ),在上面的例子中,這是一個(gè)角度有時(shí)當(dāng)我們分析交替波形時(shí),我們可能需要知道相量的位置,代表特定時(shí)刻的交替量,特別是當(dāng)我們想要的時(shí)候比較同一軸上的兩個(gè)不同波形。例如,電壓和電流。我們在上面的波形中假設(shè)波形在時(shí)間 t = 0 時(shí)開始,相應(yīng)的相位角為度或弧度。
但是如果第二個(gè)波形從左邊開始或者在這個(gè)零點(diǎn)的右邊或者我們想用相量表示法表示兩個(gè)波形之間的關(guān)系,那么我們需要考慮波形的這個(gè)相位差Φ。請考慮上一個(gè)相位差異教程中的下圖。
正弦波形的相位差
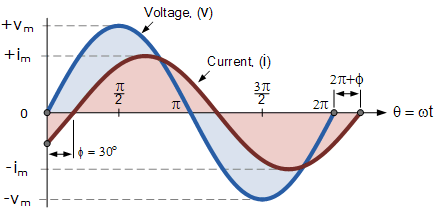
定義這兩個(gè)正弦量的廣義數(shù)學(xué)表達(dá)式將是寫作:
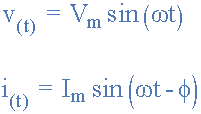
當(dāng)前, i 滯后于電壓, v 按角度Φ,在上面的例子中,這是 30 o 。因此,表示兩個(gè)正弦量的兩個(gè)相量之間的差異是角度Φ,并且得到的相量圖將是。
正弦波形的相量圖
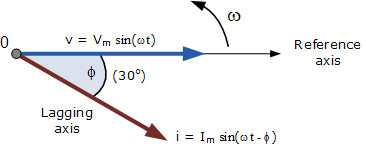
相對于水平軸上的時(shí)間零點(diǎn)( t = 0 )繪制相量圖。相量的長度與繪制相量圖的瞬間電壓,(V)和電流(I)的值成比例。電流相量滯后于角度Φ,因?yàn)閮蓚€(gè)相量如前所述沿逆時(shí)針方向旋轉(zhuǎn),因此角度Φ也以相同的逆時(shí)針方向測量。

但是,如果波形在時(shí)間凍結(jié), t = 30 o ,相應(yīng)的相量圖看起來就像右邊所示。由于兩個(gè)波形具有相同的頻率,電流相量再次落后于電壓相量。
然而,由于電流波形現(xiàn)在正在越過水平零軸線,我們可以使用電流相量作為我們的新參考,并且正確地說電壓相量“引導(dǎo)”電流相量的角度Φ。無論哪種方式,一個(gè)相量被指定為參考相量,并且所有其他相量將相對于該參考超前或滯后。
相量加法
有時(shí),在研究正弦曲線時(shí),必須將兩個(gè)交替的波形加在一起,例如在AC串聯(lián)電路中,它們彼此不同相。如果它們是同相的,則沒有相移,那么它們可以以與DC值相同的方式加在一起,以找到兩個(gè)矢量的代數(shù)和。例如,如果分別為50伏和25伏的兩個(gè)電壓“同相”,它們將相加或相加形成一個(gè)75伏(50 + 25)的電壓。
然而,如果,它們不是同相的,也就是說,它們沒有相同的方向或起點(diǎn),那么需要考慮它們之間的相位角,因此使用相量圖將它們加在一起以確定它們的結(jié)果相量或矢量和使用平行四邊形法。
考慮兩個(gè)交流電壓, V 1 具有20伏的峰值電壓, V 2 具有30伏的峰值電壓,其中 V 1 通過 60 o 引導(dǎo) V 2 。兩個(gè)電壓的總電壓 V T 可以通過首先繪制表示兩個(gè)矢量的相量圖然后構(gòu)建其中兩個(gè)邊是其中的平行四邊形來找到。電壓, V 1 和 V 2 ,如下所示。
Phasor增加兩個(gè)相量
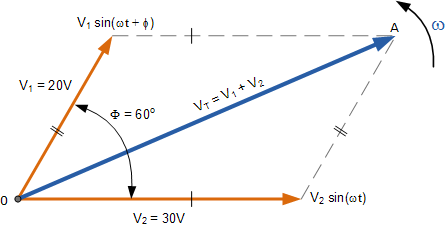
通過繪制兩個(gè)相量來縮放到方格紙上,它們的相量和 V 1 + V 2 可以通過測量對角線的長度,稱為“合成r-向量”,從零點(diǎn)到施工線的交叉點(diǎn) 0-A 。這種圖形方法的缺點(diǎn)是在繪制相量以進(jìn)行縮放時(shí)非常耗時(shí)。
此外,雖然這種圖形方法給出的答案對于大多數(shù)目的來說足夠準(zhǔn)確,但如果不是這樣,它可能會(huì)產(chǎn)生錯(cuò)誤。準(zhǔn)確或正確地繪制。然后,通過分析方法確保始終獲得正確答案的一種方法。
在數(shù)學(xué)上我們可以通過首先找到它們的“垂直”和“水平”方向?qū)蓚€(gè)電壓加在一起,然后由此我們可以計(jì)算得到的“r向量”的“垂直”和“水平”分量,<跨度> V <子>? 。這種使用余弦和正弦規(guī)則來找到該結(jié)果值的分析方法通常稱為矩形形式。
在矩形形式中,相量被分成實(shí)部, x 和虛部, y 形成廣義表達(dá)式 Z = x±jy 。 (我們將在下一個(gè)教程中更詳細(xì)地討論這個(gè)問題)。然后,這給出了一個(gè)表示正弦電壓的幅度和相位的數(shù)學(xué)表達(dá)式:
復(fù)雜正弦波的定義
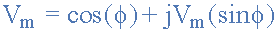
因此,使用先前的通用表達(dá)式添加兩個(gè)向量 A 和 B 如下:
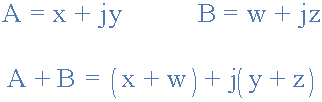
使用矩形形式的相量加法
電壓, V 2 沿參考方向的30伏電壓點(diǎn)水平零軸,然后它有一個(gè)水平分量但沒有垂直分量如下。
?水平分量 = 30 cos 0 o = 30伏
?垂直分量 = 30 sin 0 o = 0伏
這給了我們電壓 V 2 的矩形表達(dá)式: 30 + j0
電壓, V 1 的20伏電壓, V 2 60 o ,然后我t具有如下水平和垂直分量。
?水平分量 = 20 cos 60 o = 20 x 0.5 = 10伏
?垂直分量 = 20 sin 60 o = 20 x 0.866 = 17.32伏
然后給出us電壓 V 1 的矩形表達(dá)式: 10 + j17.32
合成電壓, V T 是通過將水平和垂直分量加在一起得到的,如下所示。
V Horizontal = V 1 和 V 2 的實(shí)部之和= 30 + 10 = 40伏
V 垂直 = V 1的虛部之和 和 V 2 = / 0 + 17.32 = 17.32伏特
現(xiàn)在已經(jīng)找到了實(shí)數(shù)和虛數(shù)值電壓 V T 僅通過使用確定對于90 o 三角形,g畢達(dá)哥拉斯定理如下。

然后得到的相量圖將是:
V T的結(jié)果值

相量減法
相量減法與上述矩形加法非常相似,不同之處在于此時(shí)矢量差是 V 兩個(gè)電壓之間平行四邊形的另一個(gè)對角線1 和 V 2 ,如圖所示。
兩個(gè)相量的矢量減法

這次不是將水平和垂直分量“加”在一起,而是將它們帶走,減法。
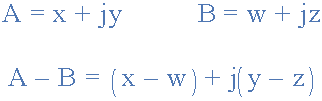
三相相量圖
以前我們只看過單個(gè)多匝線圈旋轉(zhuǎn)的單相交流波形在磁場中。但是,如果三個(gè)相同的線圈匝數(shù)相同的線圈在相同的轉(zhuǎn)子軸上以120 o 的電角度放置,則會(huì)產(chǎn)生三相電壓供應(yīng)。
平衡三相電壓源由三個(gè)單獨(dú)的正弦電壓組成,這些電壓在幅度和頻率上都相等,但彼此之間的電相位相差正好120 o 。
標(biāo)準(zhǔn)做法是將三個(gè)階段的顏色編碼為紅色,黃色和藍(lán)色,以識(shí)別每個(gè)階段紅相作為參考相。三相電源的正常旋轉(zhuǎn)順序?yàn)榧t色,然后是黃色,然后是藍(lán)色,( R , Y , B )。
與上面的單相相量一樣,代表三相系統(tǒng)的相量也以逆時(shí)針方向旋轉(zhuǎn)圍繞中心點(diǎn)的方向,如標(biāo)記為ω的箭頭所示,單位為rad / s。三相平衡星形或三角形連接系統(tǒng)的相量如下所示。
三相相量圖

相電壓的大小都相等,但相位角只有不同。線圈的三個(gè)繞組在點(diǎn)處連接在一起,a 1 ,b 1 和c 1 以產(chǎn)生三個(gè)共同的中性連接個(gè)別階段。然后,如果將紅相作為參考相,則可以相對于公共中性點(diǎn)定義每個(gè)單獨(dú)的相電壓。
三相電壓方程

如果紅色相電壓 V RN 被視為前面所述的參考電壓,那么相序?qū)⑹?R - Y - B 所以黃相中的電壓滯后 V RN 120 o ,藍(lán)相中的電壓也滯后 V YN 也是120 o 。但我們也可以說藍(lán)相電壓 V BN 導(dǎo)致紅相電壓 V RN 120 o 。
關(guān)于三相系統(tǒng)的最后一點(diǎn)。由于三個(gè)單獨(dú)的正弦電壓在120 o 之間具有固定的關(guān)系,因此它們被稱為“平衡”,因此,在一組平衡的三相電壓中,它們的相量和總是為零: V a + V b + V c = 0
Phasor Diagram Summary
然后總結(jié)本教程關(guān)于Phasor Diagrams的一些內(nèi)容。
最簡單的說,相量圖是旋轉(zhuǎn)矢量在水平軸上的投影,代表橫軸瞬時(shí)值。由于可以繪制相量圖來表示任何時(shí)刻,因此任何角度,交替量的參考相量總是沿正x軸方向繪制。
矢量,相量和相量圖僅適用于正弦交流交流量。
>相量圖可用于在任何時(shí)刻表示兩個(gè)或多個(gè)固定的正弦量。
通常,參考相量沿著水平軸并在該時(shí)刻繪制其他相量。所有相量均以水平零軸為參考。
可繪制相量圖以表示兩個(gè)以上的正弦曲線。它們可以是電壓,電流或其他一些交替量,但它們的頻率必須相同。
所有相量都沿逆時(shí)針方向旋轉(zhuǎn)。參考相量之前的所有相量都稱為“前導(dǎo)”,而參考相量后面的所有相量都稱為“滯后”。
通常,相量的長度代表均方根
由于矢量的速度不同,不同頻率的正弦曲線不能在相同的相量圖上表示,這是正弦曲線的數(shù)值而不是其最大值。 。在任何時(shí)刻,它們之間的相位角都會(huì)不同。
可以將兩個(gè)或多個(gè)向量相加或相減,成為單個(gè)向量,稱為a結(jié)果向量。
向量的水平邊等于實(shí)數(shù)或“x”向量。矢量的垂直邊等于虛數(shù)或“y”矢量。合成的直角三角形的斜邊相當(dāng)于“r”向量。
在三相平衡系統(tǒng)中,每個(gè)單獨(dú)的相量移位120 o 。
在下一篇關(guān)于 AC Theory 的教程中,我們將把正弦波形表示為矩形形式的復(fù)數(shù),Polar形式和指數(shù)形式。
-
正弦波
+關(guān)注
關(guān)注
11文章
638瀏覽量
55263 -
教程
+關(guān)注
關(guān)注
25文章
265瀏覽量
54131 -
波形
+關(guān)注
關(guān)注
3文章
378瀏覽量
31506 -
交流電路
+關(guān)注
關(guān)注
0文章
182瀏覽量
28811 -
相量圖
+關(guān)注
關(guān)注
0文章
7瀏覽量
6941
發(fā)布評(píng)論請先 登錄
相關(guān)推薦
電源技術(shù)之正弦波形(二)
相量法
三相正弦波脈寬調(diào)制(SPWM)信號(hào)發(fā)生器SM2001
正弦穩(wěn)態(tài)交流電路相量的研究
三相正弦波脈寬調(diào)制(SPWM)信號(hào)發(fā)生器SM2001
正弦穩(wěn)態(tài)電路的相量模型的詳細(xì)資料說明
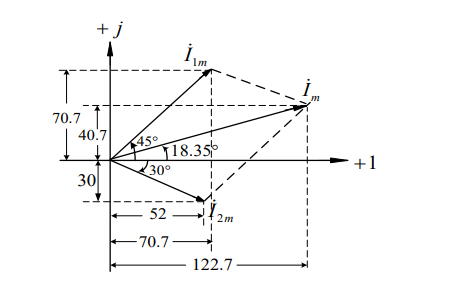
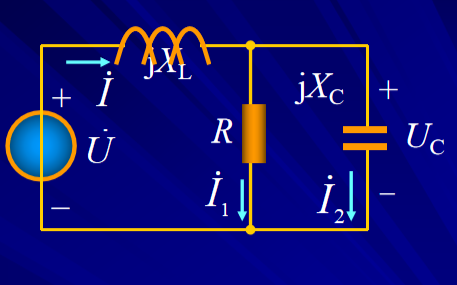
電路原理相量法的教程課件免費(fèi)下載




 正弦波形的相量圖定義和相量代數(shù)方程教程
正弦波形的相量圖定義和相量代數(shù)方程教程

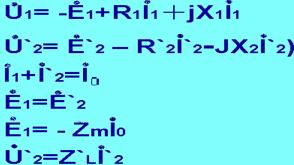











評(píng)論