基爾霍夫的電流定律（KCL）是基爾霍夫的第一個定律，用于處理進入和離開結的電荷守恒。

確定電流周圍的電流量或大小或電子電路，我們需要使用某些法律或規則，允許我們以等式的形式記下這些電流。所使用的網絡方程式是根據基爾霍夫定律的方程式，當我們處理電路電流時，我們將研究基爾霍夫的當前定律（KCL）。

Gustav Kirchhoff的現行定律是用于電路分析的基本定律之一。他的現行法律規定，對于并聯路徑，進入電路結的總電流恰好等于離開相同結的總電流。這是因為它沒有其他地方可以去，因為沒有電荷丟失。

換句話說，所有進入和離開結點的電流的代數和必須等于零：ΣI IN =ΣI OUT 。

基爾霍夫的這個想法通常被稱為充電守恒，因為電流在結點周圍保守而沒有電流損失。讓我們看一下Kirchhoff當前定律（KCL）應用于單個連接點的簡單示例。

單個連接點

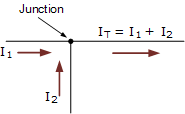
這個簡單的單結示例中，離開結點的電流 I T 是兩個電流的代數和， I 1 和 I 2 進入同一個交叉點。那是 I T = I 1 + I 2 。

請注意我們可以也正確地將其寫為代數和： I T - （I 1 + I 2 ）= 0 。

所以，如果我 1 等于3安培且I 2 等于2安培，那么總電流I T 離開結點將是3 + 2 = 5安培，我們可以將此基本定律用于任意數量的結點或節點，因為進入和離開的電流總和將相同。

此外，如果我們顛倒了電流的方向，對于I 1 或I 2 ，得到的方程仍然適用。當我 1 = I T -I 2 = 5-2 = 3安培，I 2 = I T -I 1 = 5-3 = 2安培。因此，我們可以將進入結點的電流視為正（+），而離開結點的電流為負（ - ）。

然后我們可以看到電流的數學總和要么進入或者離開交叉點并且在任何方向上總是等于零，這形成了基爾霍夫連接規則的基礎，更常見的是基爾霍夫的當前定律或（KCL）。

并聯電阻

讓我們看看我們如何將Kirchhoff的電流定律并聯應用于電阻，無論這些分支中的電阻是相等還是不相等。請考慮以下電路圖：

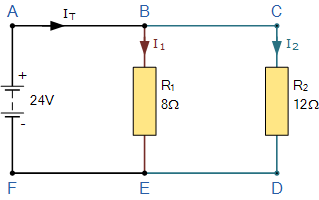
在這個簡單的并聯電阻器示例中，有兩個不同的電流結。結點1發生在節點B處，結點2發生在節點E處。因此，我們可以使用基爾霍夫結點規則來處理這兩個不同結點的電流，對于那些進入結點的電流以及流向結點的電流。 / p>

首先，所有電流，I T 離開24伏電源并到達A點，然后從那里進入節點B.節點B是一個結，因為電流現在可以分成兩個不同的方向，一些電流向下流動并通過電阻器R 1 ，其余部分繼續通過電阻器R 2 通過節點C繼續。注意電流流動進入和離開節點通常稱為分支電流。

我們可以使用歐姆定律來確定通過每個電阻的各個分支電流：I = V / R，因此：

對于電流分支B至E，通過電阻R 1

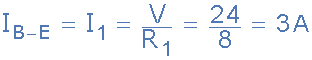
對于電流分支C至D通過電阻R <子> 2

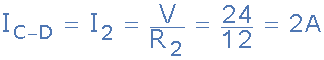
從上面我們知道基爾霍夫的現行定律表明，進入結的電流之和必須等于離開結的電流之和，在上面的簡單例子中，有一個電流I T 進入節點B的結點，兩個電流離開結點，I 1 ，I 2 。

由于我們現在從計算中知道離開節點B處的結的電流是I 1 等于3安培而I 2 等于2安培，進入節點B的結點的電流必須等于3 + 2 = 5安培。因此Σ IN = I T = 5安培。

在我們的例子中，我們在節點B和節點E有兩個不同的連接點，因此我們可以確認I T 的這個值，因為兩個電流在節點E再次重新組合。因此，對于Kirchhoff的連接規則保持為真，進入F點的電流之和必須等于流出的電流之和節點E的連接點。

由于進入結E的兩個電流分別為3安培和2安培，因此進入F點的電流之和為：3 + 2 = 5安培。因此Σ IN = I T = 5安培，因此基爾霍夫電流定律成立，因為它與當前離開點A的值相同。

將KCL應用于更復雜的電路。

我們可以使用基爾霍夫電流定律來找到在更復雜電路周圍流動的電流。我們希望現在知道節點（連接點）處的所有電流的代數和等于零，并且考慮到這個想法，這是確定進入節點和離開節點的電流的簡單情況。考慮下面的電路。

基爾霍夫的現行法律例子No1

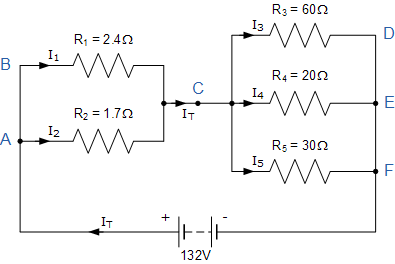
在這個例子中是電流在節點A，C，E和節點F處分開或合并在一起的四個不同的結點。電源電流I T 在流過電阻器R 1 和R 2 ，在節點C重新組合，然后再次通過電阻器R 3 ，R 4 和R 5 分離最后在節點F再次重新組合。

但在我們計算流過每個電阻支路的各個電流之前，我們必須首先計算電路總電流I T 。歐姆定律告訴我們I = V / R并且我們知道V的值，132伏，我們需要計算電路電阻如下。

電路電阻R AC

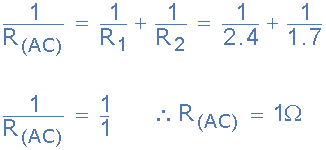
因此節點A和C之間的等效電路電阻計算為1歐姆。

電路電阻R CF

>

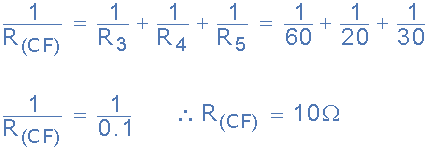
因此節點C之間的等效電路電阻并且F計算為10歐姆。然后總電路電流I T 給出如下：

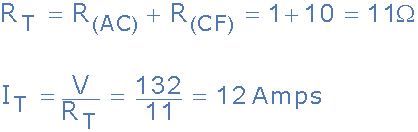
給我們一個等效電路：

基爾霍夫電流定律等效電路

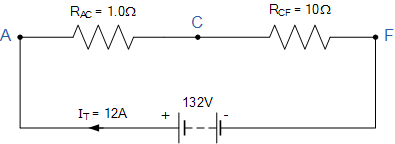
因此，V = 132V，R AC =1Ω，R CF =10Ω，I T = 12A。

建立等效并聯電阻和電源電流后，我們可以現在計算各個分支電流并使用Kirchhoff的連接規則確認如下。

因此，我 1 = 5A，I 2 = 7A，I 3 = 2A，I 4 = 6A，I 5 = 4A。

我們可以通過使用節點C作為我們的參考點來計算進入和離開結點的電流，確認Kirchoff的電流定律適用于電路：

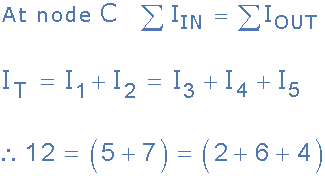
我們還可以仔細檢查Kirchhoffs Current Law是否適用，因為進入交叉點的電流是正的，而離開的是周四，路口是負面的代數和是：I 1 + I 2 -I 3 -I 4 -I 5 = 0等于5 + 7 - 2 - 6 - 4 = 0.

因此我們可以通過分析證實基爾霍夫電流定律（KCL）表明電流的代數和在這個例子中，電路網絡中的連接點始終為零是正確的。

基爾霍夫電流定律示例No2

使用基爾霍夫電流定律求出在后續電路周圍流動的電流僅

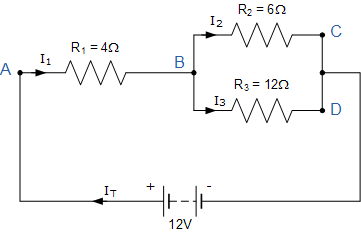
I T 是由12V電源電壓驅動的電路周圍的總電流。在A點， I 1 等于 I T ，因此會有 I 1 * R 電阻R 1 上的電壓降。

該電路有2個分支，3個節點（B，C和D）和2個獨立的循環，因此兩個循環周圍的I * R電壓降將是：

循環ABC?12= 4I 1 + 6I 2

循環ABD?12= 4I 1 + 12I 3

由于基爾霍夫現行法律規定在節點B處， I 1 = I 2 + I 3 ，因此我們可以用兩個當前的I 1 代替（I 2 + I 3 ）跟隨循環方程，然后簡化。

基爾霍夫環路方程

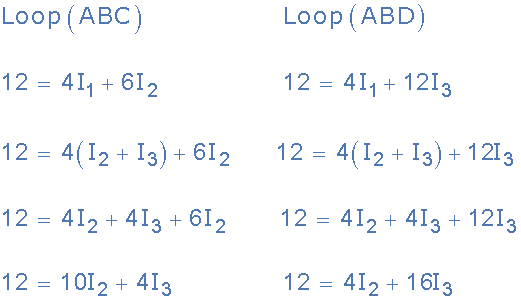
我們現在有兩個與在電路周圍流動的電流有關的聯立方程。

Eq。否1： 12 = 10I 2 + 4I 3

等式No 2： 12 = 4I 2 + 16I 3

將第一個等式（循環ABC）乘以4并且從循環ABC中減去Loop ABD，我們可以減少這兩個方程，得到 I 2 和 I 3 的值

等式否1： 12 = 10I 2 + 4I 3 （x4）? 48 = 40I 2 + 16I <子> 3

等式No 2： 12 = 4I 2 + 16I 3 （x1）? 12 = 4I 2 + 16I <子> 3

等式沒有1-Eq。否2? 36 = 36I 2 +0

用術語替換 I 2 of I 3 為我們提供 I 2 的值為 1.0Amps

現在我們可以通過將第一個等式（循環ABC）乘以4和第二個等式（Loop）來執行相同的過程來找到 I 3 的值再次通過從Loop ABD中減去Loop ABC，我們可以減少兩個方程，得到 I 2 和 I 的值3

等式否1： 12 = 10I 2 + 4I 3 （x4）? 48 = 40I 2 + 16I <子> 3

等式否2： 12 = 4I 2 + 16I 3 （x10）? 120 = 40I 2 + 160I <子> 3

等式沒有2-Eq。否1? 72 = 0 + 144I 3

因此替換 I 3 in術語 I 2 為我們提供 I 3 的值為 0.5Amps

正如Kirchhoff的交叉規則所述： I 1 = I 2 + I 3

流過電阻器 R 1 的電源電流如下： 1.0 + 0.5 = 1.5Amps

因此 I 1 = I T = 1.5Amps ， I 2 = 1.0Amps 和 I 3 = 0.5Amps 根據該信息，我們可以計算出器件和電路周圍各點（節點）的I * R壓降。

我們可以簡單而簡單地使用歐姆定律解決了示例二的電路，但我們在這里使用基爾霍夫電流定律來說明如何解決更復雜的電路當我們不能簡單地應用歐姆定律時。