節點電壓分析發現不同節點之間的電路周圍未知電壓降,為兩個或多個電路元件提供公共連接
節點電壓分析補充了以前的網格分析,它同樣強大,并基于相同的矩陣分析概念。顧名思義,節點電壓分析使用Kirchhoff第一定律的“Nodal”方程來找出電路周圍的電壓電位。
所以通過將所有這些節點電壓加在一起凈結果將等于零。然后,如果電路中有“n”個節點,則會有“n-1”個獨立的節點方程,僅這些就足以描述并因此解決電路。
在每個節點處寫下Kirchhoff的第一定律方程,即:“進入節點的電流與離開節點的電流的值完全相等”然后根據分支上的電壓表示每個電流。對于“n”個節點,一個節點將用作參考節點,所有其他電壓將相對于該公共節點進行參考或測量。
例如,考慮上一節中的電路。
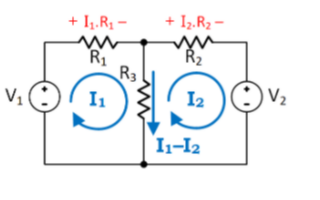
節點電壓分析電路
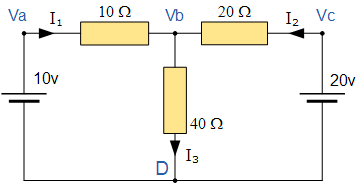
在上面的電路中,節點 D選擇作為參考節點,假設其他三個節點相對于節點 D具有 Va,Vb 和 Vc 的電壓。例如;
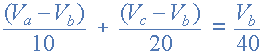
當 Va = 10v 且 Vc = 20v , Vb 可以通過以下方式輕松找到:
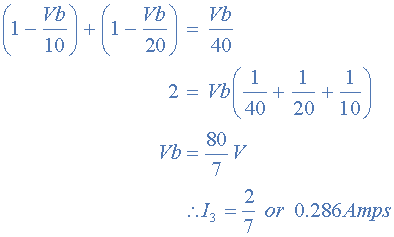
相同的 0.286amps 值,我們在前一個教程中使用了Kirchhoff的Circuit Law。
從我們到目前為止看到的網格和節點分析方法來看,這是最簡單的解決這個特定電路的方法。通常,當周圍存在大量電流源時,節點電壓分析更合適。然后將網絡定義為:[ I ] = [ Y ] [ V ]其中[ I ]為驅動電流源[ V ]是要找到的節點電壓,[ Y ]是在[ V 上運行的網絡的導納矩陣]給[ I ]。
節點電壓分析摘要
求解Nodal分析方程的基本步驟如下:
1。記下當前向量,假設流入節點的電流為正。即,“N”個獨立節點的( N x 1 )個矩陣。
2.寫入導納矩陣[網絡的Y ]:
Y 11 =第一個節點的總導納。
Y 22 =第二個節點的總導納。
R JK =總數準入加入節點 J 到節點 K 。
3。對于網絡“N”個獨立節點,[ Y ]將是( N x N )矩陣, Ynn 將為正且 Yjk 將為負值或零值。
4。電壓矢量將為( N x L )并列出要找到的“N”電壓。
我們現在已經看到了許多簡化線性電路分析的定理。在下一個教程中,我們將看看Thevenins定理,該定理允許由線性電阻和源組成的網絡由具有單個電壓源和串聯電阻的等效電路表示。
-
電路
+關注
關注
172文章
5849瀏覽量
171909 -
節點電壓
+關注
關注
1文章
20瀏覽量
1902
發布評論請先 登錄
相關推薦
單級功率因數校正電路的直流母線電壓分析和實驗研究
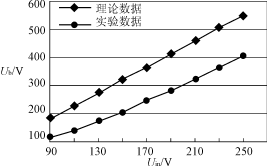
220kv電力變壓器正反調和粗細調沖擊電壓分析





 節點電壓分析電路
節點電壓分析電路










評論