在上一篇文章中，我們研究了使用不同計算器計算表面和嵌入式微帶跡線阻抗時可能出現的不一致。前一篇文章中提到的許多相同問題都適用于帶狀線阻抗計算器。對稱帶狀線比非對稱帶狀線更容易解決，無論是數字還是分析。在這里，我們將對對稱帶狀線的各種阻抗公式和計算器進行簡短比較。

IPC公式和Wadell方法

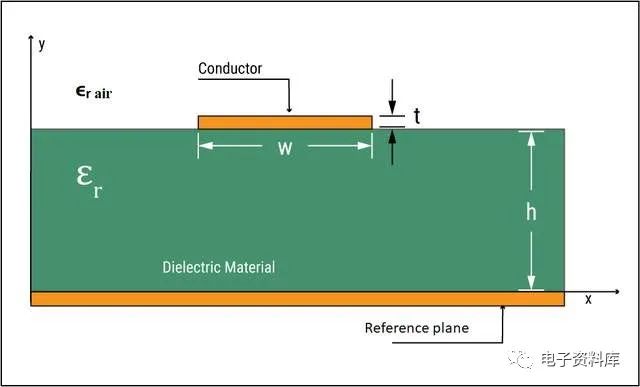
就像在微帶阻抗計算器的情況下，帶狀線阻抗計算器往往依賴于IPC-2141公式或Wadell方程。應始終仔細檢查計算器是否在適當的近似值下實現這些方程式。首先，本文中的等式中使用的符號對應于下面顯示的幾何：

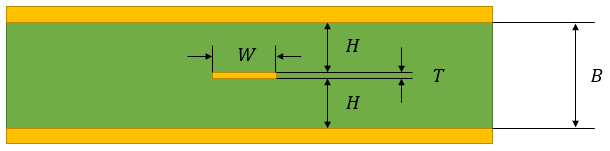
對稱帶狀線幾何

許多計算器將方程式劃分為一系列近似值，用于上圖中幾何參數的各種限制。可以使用Wadell的方法找到這些方程。在特定（非互斥）近似下，以下等式定義帶狀線的阻抗：

帶狀線窄條的阻抗方程

對于寬微帶，上述方程就條紋電容系數而言減少到下式：

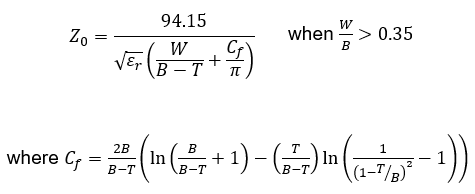
寬帶的帶狀線阻抗方程

上述解決方案在IPC中明確定義2141標準。通常，這些方程在實驗結果中產生約1％的誤差，這比微帶傳輸線的IPC標準方程高得多。這是IPC-2141標準明確使用正確定義的一個領域。

一個好的計算器將自動區分相關限制并根據用戶的輸入應用正確的方程。其他人會假設用戶指的是窄帶或寬帶狀線，但它不會明確說明計算器的適用性。在計算帶狀線的阻抗時，務必檢查計算器是否定義了上述兩個限制之一。

某些計算器直接相互模擬，因此可能包含相同的印刷錯誤。還有其他方程為帶狀線阻抗計算器定義，僅在特定近似值下有效，并且它們實際上是上述等式的減少。作者認為應避免使用其他方程。

極限T = 0的替代解決方案可以用第一類橢圓積分表示。對創建自己的帶狀線計算器感興趣的開發人員可以輕松實現用于評估此積分的標準數值算法。有興趣的讀者可以參考科恩關于該等式的主題的原始論文。

與傳輸線的關系

一個經常被解決的方面 - 兩者都是微帶和帶狀線充當傳輸線 - 這兩個公式是否實際上是一致的，應該使用哪些公式。事實上，基于電路分析的傳輸線特性阻抗方程與Wadell方法定義的阻抗之間并沒有真正的爭議。使用電路分析中的傳輸線方程的問題來自于計算集總傳輸線模型中的等效參數。

作為復習，傳輸線的阻抗與每單位電感和傳輸線的電容。請注意，這適用于微帶線或帶狀線傳輸線。通常，損耗被認為是銅導體具有一些小電阻，并且襯底在傳輸線與其參考平面之間提供一些殘余電導。有損傳輸線單端阻抗的基本公式如下所示。

傳輸線通過電路分析確定的阻抗方程

該等式來自傳輸線的等效集總元件電路模型。注意，該等式中的等效電容和電感與傳輸線的幾何形狀以及導體和基板的材料特性有關。由于多種原因，在帶狀線和微帶阻抗方程的每個推導中都沒有明確說明這一點。

首先，返回平面中電流的確切路徑決定了等效電路的環路電感，而參考平面中的電流的橫向分布決定了電容。橫向電流分布也與襯底電導有關。假設電流分布均勻分布在參考平面中，并且電流返回路徑沿導體精確跟隨并不總是正確的。因此，使用幾何近似不是計算傳輸線的集總電容和電感的最佳方法。

有些計算器允許您輸入每單位長度的等效電感和電容，以及在計算帶狀線或微帶傳輸線的阻抗時，導體的電阻，基板電導和信號頻率。然而，這些值不能先驗地知道并且需要精確的測量。因此，Wadell概述的方法是計算帶狀線或微帶阻抗的更精確的方法。

如果您正在尋找有用的資源來設計具有矩形或圓形橫截面的傳輸線， IEEE論文提供了一個很好的起點和一些簡單的公式。本文中的公式是在合理的近似值下得出的，與PCB中的實驗結果一致。

高速和高頻控制阻抗設計非常重要且節省大量時間，您需要允許的設計工具您可以為帶狀線配置定義正確的阻抗方程。 Altium Designer包括一個層堆棧管理器和阻抗計算器，帶有廣泛的堆棧材料庫。您將擁有將幾何圖形約束到控制整個PCB阻抗所需尺寸所需的工具。