|
在分析或設計系統時,二階系統的響應特性常被視為一種基準。雖然在實際中幾乎沒有二階系統,而是三階或更高階系統,但是它們有可能用二階系統去近似,或者其響應可以表示為一、二階系統響應的合成。因此,將對二階系統的響應進行重點討論。
典型的二階系統的方框圖如圖3-6所示,它由一個非周期環節和一個積分環節串聯組成,系統的傳遞函數為
令
則
從上式不難求得閉環系統的極點為
 |
(3-12) |
式中?ζ :阻尼比
????ωn:無阻尼自然振蕩角頻率
振蕩角頻率ωd的單位本為rad/s,但因弧度本身無量綱,只表示比值的概念。在研究控制系統時習慣上寫為s-1,同時也常簡稱ωd為頻率。
由式(3-12)可知,系統極點的實部為σ,它控制著時間響應的暫態分量是發散還是衰減,以及暫態分量隨時間的變化率。當σ>0時,暫態響應隨時間增長而發散,當σ<0時,暫態響應隨時間增長而衰減。由于σ=-ζωn,且ωn不可能為負值,所以,又可以看出,當 ζ<0時,系統暫態響應將隨時間增長而發散,而當 ζ>0時,系統暫態響應才能隨時間增長而衰減。
當阻尼比ζ=1時,系統具有兩重實極點,于是系統暫態響應中沒有周期分量,暫態響應將隨時間按指數函數規律而單調衰減。此時稱系統處于臨界阻尼情況。
當ζ=0時,系統將具有一對純虛數極點,其值為s1,s2=±jω此時稱系統處于無阻尼狀態,系統的暫態響應將是恒定振幅的周期函數,并且將 稱為無阻尼自然振蕩角頻率,或簡稱為無阻尼自然振蕩頻率。
當0< ζ<1時,系統具有一對實部為負的復數極點,系統的暫態響應將是振幅隨時間按指數函數規律衰減的周期函數,此時稱系統處于欠阻尼狀態。
在圖3-7中表示出當 為不同值時,相應系統極點的分布與階躍響應的圖形。
(a) ζ>1(左半平面有相異實根)時系統響應
(b) ζ=1(左半平面有相同實根)時系統響應
(c)0< ζ<1(左半平面有帶負實根的共軛虛根)時系統響應
(d)ζ =0(虛軸上帶共軛虛根)時系統響應
(e)0>ζ >-1(右半平面有帶正實根的共軛虛根)時系統響應
(f) ζ<-1(右半平面有相異正實根)時系統響應
圖3-8說明系統極點的位置與ζ 、ωn 、σ及ωd之間的關系。對于標出的一對共軛復數極點ωn是從極點到s平面原點的徑向距離,σ是極點的實部,ωd是極點的虛部,而阻尼比ζ等于極點到s平面原點間徑向線與負實軸之間夾角的余弦,即 ζ=cosθ
阻尼比ζ是二階系統的重要特征參量。
3.5.1二階系統的單位階躍響應
下面分析過阻尼、臨界阻尼和負阻尼三種情況下,二階系統的單位階躍響應。
(1) 欠阻尼情況( 0< ζ<1 )
????此時
式中 ,ωd頻率叫阻尼自然頻率。對于單位階躍輸入,C(s)可以寫成 ,ωd頻率叫阻尼自然頻率。對于單位階躍輸入,C(s)可以寫成
為求出上式的拉普拉斯反變換,將上式寫成下列形式
其拉普拉斯反變換為
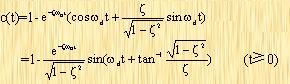 |
(3-13) |
由上式可以看出,暫態振蕩頻率為阻尼自然頻率,它是隨阻尼比ζ而變化的。這一系統的誤差信號,是輸入量與輸出量之差,即
顯然,這個誤差信號為一阻尼正弦振蕩。穩態時或t=∞時,輸入量與輸出量之間不存在誤差。
如果阻尼比ζ等于零,那么系統的響應變為無阻尼等幅振蕩。將ζ=0值代入(3-13),便可得到零阻尼情況下的響應c(t),即
從上式可以看出,ωn代表系統的無阻尼自然頻率。即如果阻尼系數減少到零時,系統將以頻率ωn振動。如果線性系統具有一定阻尼,就不可能通過實驗得到無阻尼自然頻率,而只能得到阻尼自然頻率ωd,ωd 等于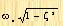 。阻尼自然頻率總是低于無阻尼自然頻率ωd。ζ值增大時,阻尼自然頻率ωd將減小。如果ζ增加到大于1,系統的響應將變成過阻尼,因而不再產生振蕩。 。阻尼自然頻率總是低于無阻尼自然頻率ωd。ζ值增大時,阻尼自然頻率ωd將減小。如果ζ增加到大于1,系統的響應將變成過阻尼,因而不再產生振蕩。
(2) 臨界阻尼情況(ζ=1)
如果C(s)/R(s)的兩個極點接近相等,則系統可近似看作臨界阻尼系統。對于單位階躍輸入量,R(s)=1/s,因而C(s)可表示為
上式的拉普拉氏反變換為:
(3) 過阻尼情況(ζ>1)
這種情況下,C(s)/R(s)的兩個極點是兩個不等的負實數。對于單位階躍輸入量,R(s)=1/s,因此C(s)可以寫成
其拉普拉斯反變換為
式中 ,而 ,而  ,顯然,這時系統的響應c(t)包含著兩個衰減的指數項。 ,顯然,這時系統的響應c(t)包含著兩個衰減的指數項。
當ζ遠大于1時,在兩個衰減的指數項中,一個比另一個衰減的要快得多,因此衰減得比較快的指數項(相應于較小時間常數的指數項),就可以忽略不計。也就是說,如果-s2與j 軸的距離比-s1要近得多(即|s1|>>|s2| ),那么在近似解中,可以忽略-s1,因為方程中包含s1的項比包含s2的項衰減得快的多,所以-s1對系統響應的影響,比-s2對系統的影響要小得多,因此忽略-s1是合理的。因此可以將C(s)/R(s)近似地表示為
這一近似函數形式是根據下述條件直接得到的,即原來的函數C(s)/R(s)與近似函數的初始值和最終值,兩者是完全相同的。
對于近似傳遞函數C(s)/R(s),其單位階躍響應可表示為
其時間響應c(t)為
在過阻尼情況下,二階系統的單位階躍響應是隨時間推移而單調增長,最后在t→∞時趨于穩態值,所以最大超調量是零,調整時間可以用近似的單位階躍響應估算,如借用一階系統單位階躍響應的性質,可以認為響應達到穩態值的95%所需的調整時間
工程上,如果ζ》1.5時,使用上述近似式已有足夠的準確度了。
3.5.2 二階系統的暫態響應指標
當系統為欠阻尼情況下,即0< ζ<1時,二階系統階躍響應的上升時間tr、峰值時間tp、最大超調量Mp的計算公式按式(3-13)可表示如下。
上升時間tr 令c(t)=1,代入式(3-13)中,即可求得tr。這時有
或
所以
 |
(3-14) |
由上式可見,如欲減小tr,當ζ一定時,需增大ωn ,反之,若ωn一定時,則需減小ζ。
峰值時間tp 出現第一個峰時,單位階躍響應隨時間的變化率為零。為求tp,可將式(3-13)對時間t求導,并令其為零。于是得
由此可知:
 |
??n=0、1、2、…… |
到達第一個峰值時應有
故得
 |
(3-15) |
最大超調量Mp 最大超調量發生在t=tp,因此,令式(3-13)中的t=tp,并將tp值代入,即得以百分比表示的超調量
 |
(3-16) |
調整時間ts 對于欠阻尼二階系統,暫態響應可由式(3-13)求得為
曲線 ,是系統對單位階躍輸入信號的暫態響應曲線的包絡線,響應曲線c(t)總是包含在一對包絡線之內,如圖3-9所示。包絡線的時間常數為1/(ζωn)。這樣,當采用5%允許誤差時,有 ,是系統對單位階躍輸入信號的暫態響應曲線的包絡線,響應曲線c(t)總是包含在一對包絡線之內,如圖3-9所示。包絡線的時間常數為1/(ζωn)。這樣,當采用5%允許誤差時,有
1+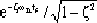 =1.05 =1.05 |
由上式得
當0< ζ< 0.8時,則有
當采用2%允許誤差時,則可推導得出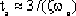
3.5.3二階系統的脈沖響應
當輸入信號r(t)為單位脈沖函數時,相應的拉普拉斯變換為1,即R(s)=1。則二階系統的單位脈沖響應C(s)為
這個方程的拉普拉斯反變換,就是時域響應解c(t),這時當0≤ζ<1時,
c(t)= ??(t≥0) ??(t≥0) |
當ζ=1時
c(t)=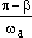 ??(t≥0) ??(t≥0) |
當ζ>1時
c(t)= ??(t≥0) ??(t≥0) |
不同ζ時單位脈沖響應曲線見圖3-10。對ζ≥1的情況,單位脈沖響應總是正值或在t=∞時為零。這時系統的單位階躍響應必是單調增長的。
由于單位脈沖響應是單位階躍響應的導數,所以單位脈沖響應曲線與時間軸第一次相交的點對應的時間必是峰值時間tp,而從t=0至t=tp這一段曲線與時間軸所包圍的面積將等于1+Mp(參見圖3-11),而且單位脈沖響應曲線與時間軸包圍的面積代數和為1。
3-10 圖示系統中 ζ=0.6,ωn =5弧度/秒。當系統受到單位階躍輸入信號作用時,試求上升時間tr、峰值時間tp、最大超調量Mp和調整時間ts。
解:根據給定的 ζ和 ωn值,可以求得ωd = 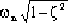 =4和 σ=ζωn =3。 =4和 σ=ζωn =3。
1. 上升時間tr
上升時間為:
tr=  = = 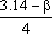
式中β為:  弧度 弧度
因此,可求得上升時間tr為:tr= 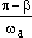 = =  秒 秒
2. 峰值時間tp
峰值時間為:
tp= 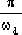 = = 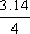 =0.785秒 =0.785秒
3. 最大超調量Mp
最大超調量為:
Mp=  = = 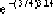 =0.095 =0.095
因此,最大超調量百分比為9.5%。
4. 調整時間ts
對于2%允許誤差標準,調整時間為:
ts= 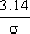 =4/3=1.33秒 =4/3=1.33秒
對于5%允許誤差標準,調整時間為:
ts= 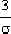 =3/3=1秒 =3/3=1秒 |  電子發燒友App
電子發燒友App

 硬聲App
硬聲App

 1419
1419
 107
107 3021
3021
 19
19 7268
7268
 10
10 1594
1594
 3
3 1
1 14
14 25
25 3257
3257 12
12 1
1 38284
38284
 99
99 30
30 54
54 12
12 24
24 1423
1423
 24
24 21
21 67
67 55
55 115
115 273
273 1630
1630
 49
49
評論