?
1.前言
數字PID控制在生產過程中是一種最普遍采用的控制方法,其特點是結構簡單,穩定性好,工作可靠,調整方便,多被應用到被控對象的結構和參數不能完全掌握或得不到精確數學模型的環境中。將數字PID控制算法應用于基站發射功率控制,可以極大地提高基站發射功率的穩定性和可靠性,控制輸出功率在覆蓋允許范圍內,不至過小無法滿足網絡規劃時的覆蓋距離要求,而減少小區覆蓋范圍,又不會產生過強的輸出信號對相鄰基站造成干擾。本文首先分析數字PID控制算法中的兩種常見算法,而后重點討論它們在基于ADUC7026的基站功率控制中的應用方法,并對比它們的測試結果,給出結論。
2.數字PID控制原理
2.1 PID控制的基本原理
?
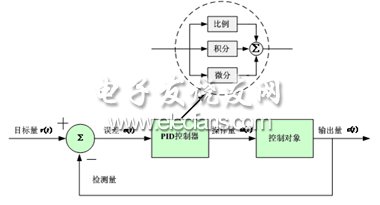
圖1 PID控制結構框圖
常規PID控制系統原理框圖如圖1所示,其控制規律為:
(1)
?
式中 為操作量, 為誤差, 為比例系數, 為積分系數, 為微分系數。簡單說來,PID控制器各校正環節的作用如下:
1. 比例環節
比例控制是一種最簡單的控制方式,控制器的輸出與輸入誤差信號成比例關系。偏差一旦產生,控制器立即產生控制作用,以減少偏差。
2. 積分環節
應用于醫用超聲的波束成形技術的定義是,由公共源產生、但由多元件超聲傳感器在不同時間接收到的所有信號的相位對齊和累加。在連續波多普勒(CWD)通道中,要對所有接收器通道進行相移和累加,然后提取相干信息。波束成形有兩個功能:它不僅能向傳感器傳遞方向性——提高其增益,而且能定義體內的焦點,并由此確定回波位置。
3. 微分環節
微分環節能反映偏差信號的變化趨勢(變化速率),并能在偏差信號值變得太大之前,在系統中引入一個有效的早期修正信號,從而加快系統的動作速度,減小調節時間[1]。
2.2 數字PID控制
為便于計算機通過軟件實現PID控制算法,在實際應用中多采用數字PID控制方式。數字PID控制算法通常又分為位置式PID控制算法和增量式PID控制算法。
2.2.1 位置式PID控制算法
按模擬PID控制算法的算式(1),以一系列的采樣時刻點kT代表連續時間t,以和式代替積分,以增量代替微分,則可做如下近似:
;
?
;
?

;
?

;
?
式中:T為采樣周期,k為采樣序號,只要采樣周期T取得足夠小,這種逼近就可以相當精確,于是可得:
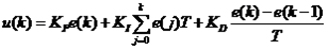
(2)
?
位置式PID控制算法使用全量輸出,所以每次輸出均與過去的狀態有關,計算時要對 進行累加,CPU輸出控制量 對應執行機構的實際位置偏差。因對 量進行累加, 可能出現大幅度變化,進而會引起執行機構的大幅度變化,這種情況在實際生產中是不允許的,在某些場合可能還會造成重大事故,因而產生了增量式PID控制算法。
2.2.2 增量式PID控制算法
當執行機構需要的是控制量的增量時,可由式(2)導出提供增量的PID控制算式。根據遞推原理可得
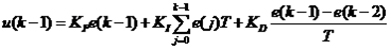
(3)
?
用式(2)減去式(3),即得到增量式PID控制算法:
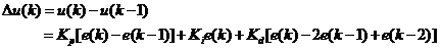
(4)
?
其中
,
,
[2]
?
3.基站功率監測系統框圖及功率控制框圖
?
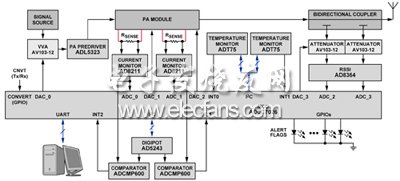
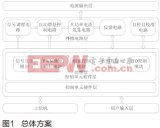
圖2 基站功率監測系統框圖
根據基站功率監測系統的各個部分的功能要求,系統的結構組成如圖2所示,射頻信號通過可調衰減器,驅動功率放大器,末級功率放大器,定向耦合器至天線發射。微控制器ADuC7026采集功率放大模塊上的兩級LDMOS的溫度和漏極電流值、功放輸出的前向功率值、反向功率值,控制器將采集到的數據傳送到PC的監控界面顯示,用戶也可通過人機交互界面調整監控系統的控制參數。ADuC7026可以為基站功率監測系統提供集成的解決方案,從而降低PCB設計的復雜度并減小PCB面積,節省系統成本,而且ADuC7026[3]支持外同步采樣,這對需要外同步采樣的TD-SCDMA應用來說非常有益。

?
圖3 自動功率控制結構框圖
圖3所示為實現自動功率控制電路的基本結構框圖,系統中輸出功率為被控對象,信號傳輸通路為一級可調衰減器和兩級放大電路。前級功率放大器采用ADI公司的ADL5323[4]來實現,該芯片的輸入輸出端已作50ohm匹配,節省了外部的阻抗匹配電路。檢波器采用ADI公司的AD8364[5],用于將采樣的功率值轉化成對應的電壓值。將采樣得到的信號功率經ADuC7026中的ADC轉化成數字信號,再經PID運算,得到控制可調衰減器的電壓,由內部DAC轉化輸出,通過調整可調衰減器的控制電壓可產生不同的衰減量,以達到驅動功率放大器的輸出功率可控的目的[6]。
4.PID算法實現
由圖3功率控制結構框圖可知,實際的輸出功率表達式如式(5)所示。
(5)
?
根據ADC轉換得到的數字電壓值轉換成采樣前的實際輸出功率值的表達式如式(6)所示。
(6)
?
其中ADC_Data為ADC的轉換結果,2.5V為ADC的參考電壓值,4096為12-bit ADC滿量程輸入值, 是AD8364的傳遞函數,10dB為耦合器的衰減量。
DAC的輸出電壓由不同PID算法的運算結果和可調衰減器的傳遞函數決定,下面介紹兩種不同PID算法的流程、程序實現及其測試結果。
4.1 位置式PID算法流程

?
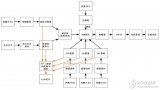
圖4 位置式PID算法流程圖
對應圖4算法流程圖,PID控制部分實現程序如下:
ActualOutputPower = 25*(float)ADCForwardPowerResult/1024-43;
Error = SetOutputPower - ActualOutputPower;
SumError += Error;
Output = Proportion*Error + Integral*SumError + Derivative* (Error – LastError);
LastError = Error;
DACVoltageValue = (float)((Output + 26.1667)*3/31);
SetDACValue = (unsigned int)(DACVoltageValue*4096/2.5);
這里,DACVoltageValue的值由輸入信號功率,兩級固定增益放大器和可調衰減器的傳遞函數決定,實際程序中給出的參數是經系統線性校正后的參數。理想情況下,假設可調衰減器的傳遞函數為:衰減量=k*控制電壓+b,輸入信號功率為pin兩級固定增益放大器的增益為g1和g2,則DAC的輸出應為式(7)所示。
(7)
?
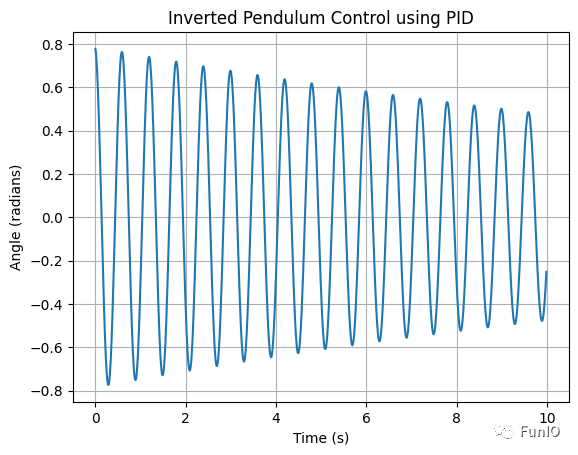
圖5所示為采用位置式PID算法,在系統輸出功率為-1dBm時,調整其輸出功率為-10dBm的實測曲線。

?
圖5 改變期望輸出功率后的變化曲線(位置式PID算法)
4.2 增量式PID算法流程
?
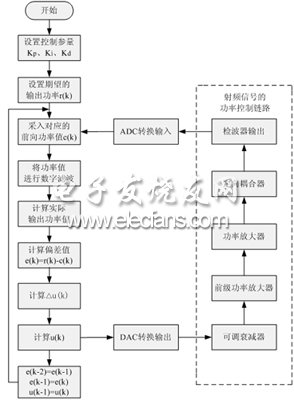
圖6 增量式PID算法流程圖
對應圖6算法流程圖,PID控制部分實現程序如下:
ActualOutputPower = 25*(float)ADCForwardPowerResult/1024-43;
Error = SetOutputPower - ActualOutputPower;
DeltaAttenuation = Proportion*(Error-LastError) + Integral*Error +
Derivative*(Error-2*LastError + PrevError);
Attenuation = DeltaAttenuation + LastAttenuation;
DACVoltageValue = (float)(Attenuation*3/31 + 3.887);
SetDACValue = (unsigned int)(DACVoltageValue*4096/2.5);
PrevError = LastError;
LastError = Error;
LastAttenuation = Attenuation;
這里,DACVoltageValue的值由可調衰減器的傳遞函數決定,實際程序中給出的參數是經系統線性校正后的參數。理想情況下,假設可調衰減器的傳遞函數為:衰減量=k*控制電壓+b,則DAC的輸出應為式(8)所示。
(8)
?
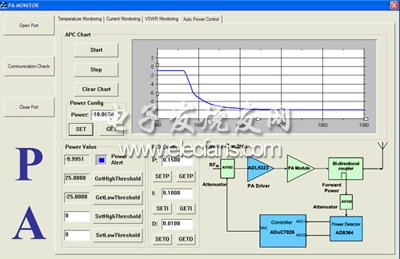
圖7所示為采用增量式PID算法,在系統輸出功率為-1dBm時,調整其輸出功率為-10dBm的實測曲線。
?
圖7 改變期望輸出功率后的變化曲線(增量式PID算法)
5.結論
由前面的測試結果可見,在同樣的測試條件下,采用位置式PID算法的時候會出現過沖的情況,增量式控制雖然只是算法上作了一點改進,卻避免了這種情況的發生。且由于計算機輸出增量,所以誤動作時影響小,必要時可用邏輯判斷的方法去掉。算式中不需要累加,控制增量 的確定僅與最近幾次的采樣值有關,所以較容易通過加權處理而獲得比較好的控制效果。因此,建議采用增量式PID算法來實現基站功率的穩定控制。
 電子發燒友App
電子發燒友App























評論