提到傅里葉變換，你是不是又想起了大學課程里被它支配的恐懼。其實，傅里葉分析不僅僅是一個數學工具，更是一種可以徹底顛覆一個人以前世界觀的思維模式。如果用方程寫一部科學史，傅里葉變換必然擁有位置，它
2023-09-11 11:21:06
289 
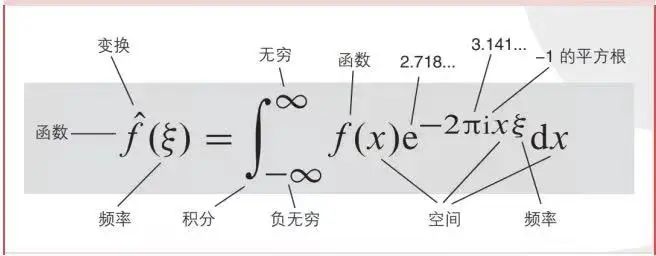
傅里葉變換與拉普拉斯變換的聯系解讀 傅里葉變換和拉普拉斯變換都是數學中非常重要的分析工具。它們都在不同的領域中發揮著重要作用。 傅里葉變換是一種將時間域信號轉換成頻率域信號的技術。它是通過將信號
2023-09-07 17:04:19219 傅里葉變換和離散傅里葉變換的關系 傅里葉變換（Fourier Transform）是一種將時間域（或空間域）的信號轉換為頻率域（或波數域）的信號的數學工具。而離散傅里葉變換（Discrete
2023-09-07 17:04:15330 短時傅里葉變換和小波變換差別 短時傅里葉變換（short-time Fourier transform，STFT）和小波變換（wavelet transform）是兩種常見的信號處理技術，它們在頻域
2023-09-07 17:04:12341 小波變換與傅里葉變換的區別和聯系? 1. 傅里葉變換和小波變換的定義 傅里葉變換（Fourier Transform，簡稱FT）是一種將信號在時域上的函數轉變為頻域上的函數的方法，對于連續時間信號
2023-09-07 17:04:07332 為什么有四種形式的傅里葉變換? 傅里葉變換是一種十分重要的數學工具，它可以將函數從時域（即時間域）轉換到頻域，從而能夠幫助人們更好地理解信號的特性。在傅里葉變換的研究過程中，出現了幾種不同的變形方式
2023-09-07 17:04:04189 傅里葉變換重要公式總結 傅里葉變換公式常用公式 傅里葉變換是一種重要的數學工具，它可以將任意周期函數分解成一系列正弦函數或余弦函數的疊加形式。這些正弦函數和余弦函數被稱為頻率分量，它們的幅度和相位
2023-09-07 16:53:083859 傅里葉變換公式理解 傅里葉變換是一種在數學、物理、工程和其他科學領域中常用的工具，它是一種將一個函數從時域轉換到頻域的方法。傅里葉變換可以將一個復雜的函數表示成一個頻域上各種周期函數的疊加，從而
2023-09-07 16:53:06534 傅里葉變換和反變換公式? 傅里葉變換和反變換在信號處理領域中被廣泛應用。傅里葉變換是將一個時域信號轉換為頻域信號的過程，而傅里葉反變換則是將一個頻域信號轉換為時域信號的過程。這篇文章將詳細講解
2023-09-07 16:53:042916 傅里葉變換的實現方法? 傅里葉變換是一種將信號在時間域和頻率域之間相互轉換的數學工具。它的實現方法有很多種，其中最常見的是離散傅里葉變換（DFT）和快速傅里葉變換（FFT）。 離散傅里葉變換是一種將
2023-09-07 16:47:52173 傅里葉變換公式總結? 傅里葉變換是一種將時域信號轉換為頻域信號的數學方法。它是通過將一個連續或離散的時域信號分解成一系列相位和幅度不同的正弦和余弦波形式，然后將它們表示到頻域中，以獲得更多的信息
2023-09-07 16:47:461222 傅里葉變換和傅里葉逆變換的關系? 傅里葉變換和傅里葉逆變換是信號處理領域中極具重要性的數學工具，它們被廣泛應用于很多領域，例如音頻、圖像處理、通信等。 傅里葉變換是將一個信號在時域（即時間或空間）上
2023-09-07 16:43:47581 正弦函數的傅里葉變換 正弦函數是數學中一種廣泛應用的基本函數，其在傅里葉分析中也是具有重要作用的函數之一。在實際應用中，我們常常需要將正弦函數進行傅里葉變換，以求得自變量函數在頻域上的表現，從而更好
2023-09-07 16:35:07836 傅氏變換和傅里葉變換的區別聯系 傅氏變換和傅里葉變換是信號處理中常用的兩種變換方法，它們有著不同的作用和特點。傅氏變換主要應用于連續時間信號的頻域分析，而傅里葉變換則主要用于離散時間信號的頻域分析
2023-09-07 16:35:05195 傅里葉變換的本質及物理意義 常用傅里葉變換性質 傅里葉變換是一種重要的數學工具，通過將一個復雜的函數表示為一系列簡單的正弦余弦函數之和，可以在許多領域應用，包括信號處理、圖像處理、物理學等。在本文
2023-09-07 16:30:33544 傅里葉變換時域平移怎么理解? 傅里葉變換是一種非常重要的數學工具，在信號處理、圖像處理、通信技術等領域中廣泛應用。其中，時域平移是傅里葉變換中一個重要的概念，需要深入理解。 時域平移的基本概念 時域
2023-09-07 16:29:40330 傅里葉變換頻移公式 傅里葉變換是一種將信號從時域轉換到頻域的數學工具。它可以將一個信號分解成一系列正弦和余弦波的和，這些正弦和余弦波的振幅和相位可以描述信號在頻域中的特性。傅里葉變換是數字信號處理
2023-09-07 16:29:36451 沖激函數時移后的傅里葉變換 傅里葉變換（Fourier transform）是數學中的一種重要的分析工具，它能夠將一個時域（time domain）或空域（space domain）中的函數轉換
2023-09-07 16:23:25396 短時傅里葉變換特點 短時傅里葉變換的意義? 短時傅里葉變換（Short-time Fourier Transform, STFT）是一種時頻分析方法，它把信號在時間和頻率上進行分解，可以對信號的短時
2023-09-07 16:23:22441 傅里葉變換的時移特性 傅里葉變換是一種非常重要的數學工具，可以將任何周期性信號或非周期性信號進行頻域分析，從而在通信、電子工程等領域中得到廣泛應用。傅里葉變換能夠將信號從時域（時間域）轉換到頻域
2023-09-07 16:23:19738 對圖像進行傅里葉變換的意義 傅里葉變換是一種將一個信號分解成其頻率分量的方法，它在信號處理、圖像處理、電信領域、計算機視覺領域等方面都有著廣泛的應用。在圖像處理領域中，傅里葉變換可以將圖像從空間域
2023-09-07 16:18:56353 傅里葉變換的數學意義 傅里葉變換是一種數學工具，它是一種將一個函數在一個頻域轉換為另一個函數在另一個頻域中的操作。傅里葉變換起源于1807年，由法國數學家讓·巴蒂斯特·約瑟夫·傅里葉提出，它是一種將
2023-09-07 16:18:51148 傅里葉變換基本性質 傅里葉變換本質 傅里葉變換的應用 傅里葉變換是現代數學、物理學、工程學等領域中非常重要的一種數學工具和基本理論。在信號處理、圖像處理、通信技術、音樂分析、光學、醫學、天氣預報等
2023-09-07 16:18:492334 傅里葉變換通俗理解 對傅里葉變換的理解? 傅里葉變換是一種數學工具，它可以將一個函數從時域（時間域）轉換到頻域（頻率域）。在數學、物理學、工程學和計算機科學等領域它被廣泛應用，例如數字信號處理
2023-09-07 16:14:41570 傅里葉變換的目的和意義 傅里葉變換幾何意義? 傅里葉變換是一種重要的數學工具和分析方法，它在信號處理、圖像處理、音頻處理等領域有著廣泛的應用。它的目的是將一個時域信號轉換為頻域信號，從而更好地理
2023-09-07 16:14:39307 傅里葉變換十大公式 傅里葉變換的十大性質? 傅里葉變換是一種重要的數學工具，在許多領域中都有廣泛的應用。傅里葉變換可以將一個時域信號轉化為頻域信號，分析不同頻率成分在信號中的占比情況。由于傅里葉變換
2023-09-07 16:14:361210 傅里葉變換對信號處理的意義? 傅里葉變換是一種基本的數學工具，它經常用于信號處理中。在這篇文章中，我們將探討傅里葉變換的意義和應用。 傅里葉變換的定義是將一個函數表示為它的頻域表示。傅里葉變換將
2023-09-07 16:14:33252 傅里葉變換有多偉大?傅里葉變換告訴我們如何解決問題? 傅里葉變換是一種數學工具，它可以將一個函數分解成一系列振幅和相位的頻率，這些頻率在某些領域 （如信號處理、圖像處理和物理學等）中被廣泛
2023-09-07 16:14:31165 傅里葉變換的意義和理解 傅里葉變換是一種將一個信號在頻域中進行分解的數學工具，它將一個信號分解為不同頻率的正弦和余弦波的疊加。傅里葉變換的基本概念源于法國數學家約瑟夫·傅里葉，而其在現代通信、圖像
2023-09-07 16:08:423549 對于一個離開課堂十余年的射頻工程師來說，傅里葉變換已經不知道埋藏在腦子里的那個角落，或者根本就沒在腦子里停留過。但無論如何，傅里葉變換對現在通信的重要性還是不言而語。當我們已經習慣用頻域去描述一個信號的時候，你可曾思考過其真實的樣子到底是什么？ 為什么這幾個短短的頻譜就可以描述一個信號 ？
2023-08-10 09:55:51341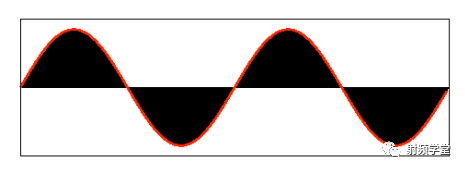 
快速傅里葉變換 (Fast Fourier Transform，FFT), 即利用計算機計算離散傅里葉變換（DFT)的高效、快速計算方法的統稱，簡稱FFT。
2023-07-20 16:46:231159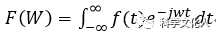 
傅里葉變換是將按時間或空間采樣的信號與按頻率采樣的相同信號進行關聯的數學公式。
2023-07-19 17:47:301830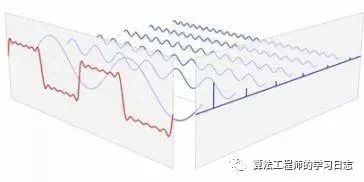 
學習傅里葉變換需要面對大量的數學公式，數學功底較差的同學聽到傅里葉變換就頭疼
2023-07-07 14:15:10217 
機器學習和深度學習中的模型都是遵循數學函數的方式創建的。從數據分析到預測建模，一般情況下都會有數學原理的支撐，比如：歐幾里得距離用于檢測聚類中的聚類。 傅里葉變換是一種眾所周知的將函數從一個域轉換
2023-06-14 10:01:16420 
傅里葉變換是一種在各個領域都經常使用的數學工具。這個網站將為你介紹傅里葉變換能干什么，為什么傅里葉變換非常有用，以及你如何利用傅里葉變換干漂亮的事。
2022-07-10 10:37:531341 各位如何用LABVIEW做一個關于離散傅里葉變換？？！！！
2012-04-08 21:59:31
周期矩陣脈沖信號傅里葉變換問題求解
2021-06-26 14:49:06
0 原信號的不同類型，傅里葉變換可以分為四種類別： (1)非周期性連續信號傅里葉變換 (2)周期性連續信號傅里葉級數 (3)非周期性離散信號離散時域傅里葉變換 (4)周期性離散信號離散傅里葉變換 快速傅里葉變換(FFT)，是利用計算機計算離散傅里葉
2020-11-09 16:52:4012009 
學習傅里葉變換需要面對大量的數學公式，數學功底較差的同學聽到傅里葉變換就頭疼。事實上，許多數學功底好的數字信號處理專業的同學也不一定理解傅里葉變換的真實含義，不能做到學以致用 事實上，傅里葉變換
2020-10-10 18:03:1721666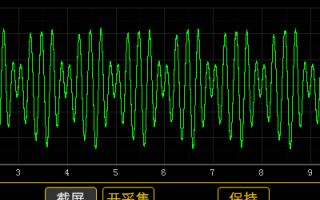 
傅里葉變換是數字信號處理領城種很重要的算法。傅里葉表明：任何連續測量的時序或信號，都可以表示為不同頻率的正弦波信號的無限疊加。而根據該原理的傅里葉變換算法利用直接測量到的原始信號，以累加方式來計算該
2019-04-30 08:00:002 主要內容：
1.傅里葉變換
2.傅里葉變換的特殊形式
3.傅里葉變換的物理意義
4.傅里葉變換存在的條件
2018-03-05 11:08:043 主要內容：
1.正弦信號的傅里葉變換
2.一般周期信號的傅里葉變換
3.如何由F0(ω)求F(nω1)
4.單位沖激序列的傅氏變換
5.周期矩形脈沖序列的傅氏變換
2018-03-05 10:59:052 詳細講述傅里葉變換和小波變換原理
2018-01-16 14:34:429 小波變換與傅里葉變換有什么區別嗎？小波變換與傅里葉變換哪個好？我們通過小波變換與傅里葉變換的詳細解讀、小波變換與傅里葉變換的區別、傅里葉變換缺點方面來解析。
2018-01-13 11:02:2213781 
抽樣信號的傅里葉變換
2017-12-06 14:36:013 傅里葉變換的性質
2017-12-06 14:35:0059 快速傅里葉變換 （fast Fourier transform）,即利用計算機計算離散傅里葉變換（DFT）的高效、快速計算方法的統稱，簡稱FFT。快速傅里葉變換是1965年由J.W.庫利
2017-11-27 16:23:011408 傅里葉級數對周期性現象做數學上的分析傅里葉變換可以看作傅里葉級數的極限形式，也可以看作是對周期現象進行數學上的分析。除此之外，傅里葉變換還是處理信號領域的一種很重要的算法。要想理解傅里葉變換算法的內涵，首先要了解傅里葉原理的內涵。
2017-11-24 14:32:4237881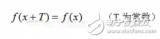 
第三章-離散傅里葉變換-作業
2016-12-28 14:23:300 第三章-離散傅里葉變換
2016-12-28 14:23:303 第3章--離散傅里葉變換(DFT)
2016-12-28 14:23:302 【檢測技術】 快速傅里葉變換，測控技術儀器必備課程，喜歡學習的朋友可以下載學習學習。
2016-11-18 16:53:481 《OpenCV3編程入門》書本配套源代碼:離散傅里葉變換
2016-06-06 15:39:445 關于短時傅里葉變換的原理及其在通信的應用。
2016-05-17 16:41:515 見過的介紹傅里葉變換的很好的文章，通俗易懂，轉發的，學習。
2016-04-29 14:12:1410 傅里葉變換的深刻理解結合書本，會有更好的效果
2015-11-26 11:29:1253 離散傅里葉變換是一種在時域和頻域均離散的傅里葉變換.
2011-02-23 09:30:1049 序列的傅里葉變換(DTFT) :DTFT:Discrete-time Fourier transform為研究離散時間系統的頻率響應作準備，從抽樣信號的傅里葉變換引出：二．傅氏變換、拉氏變換、z變換的關系1. 三
2009-09-30 19:38:2536 非周期信號的傅里葉變換
前面已討論了周期非正弦信號的傅里葉級數展開，下面來分析非周期信號的傅里葉變換。當周期
2009-07-27 10:23:307992 離散傅里葉變換及其快速算法離散傅里葉變換 (Discrete Fourier Transform，DFT)是時間函數是離散的，而且頻譜函數也是離散的變換。3. 1 討論周期序列的 傅里葉級數及其性質。
2008-10-30 12:54:5433 從本章開始由時域轉入變換域分析，首先討論傅里葉變換。傅里葉變換是在傅里葉級數正交函數展開的基礎上發展而產生的，這方面的問題也稱為傅里葉分析（頻域分析）。將信號
2008-08-05 11:49:3750 傅里葉變換公式
2007-11-29 12:52:35494 傅里葉變換詳解
2007-11-29 12:48:014
電子發燒友App
工商網監
評論