第十五講 組合邏輯電路的分析方法和設計方法

6.1概述
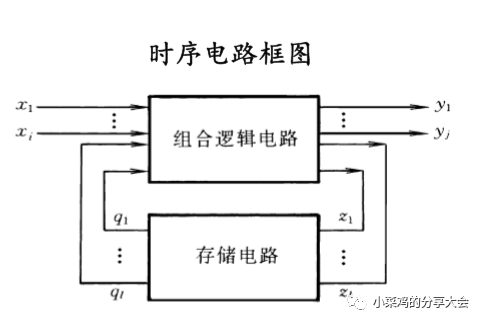
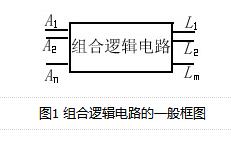
組合邏輯電路：
定義
構成
電路特點
6.2.1組合邏輯電路的分析方法
一、基本分析方法
分析：給定邏輯電路，求電路的邏輯功能。
步驟：
二、分析舉例
歸納總結：
6.2.2 組合邏輯電路的設計方法

一、基本設計方法
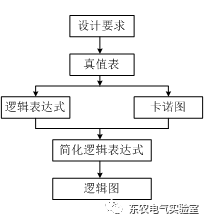
設計：設計要求→邏輯圖。
步驟（與分析相反）:
二、設計舉例
1．單輸出組合邏輯電路的設計
2．多輸出組合邏輯電路的設計

6.1概述

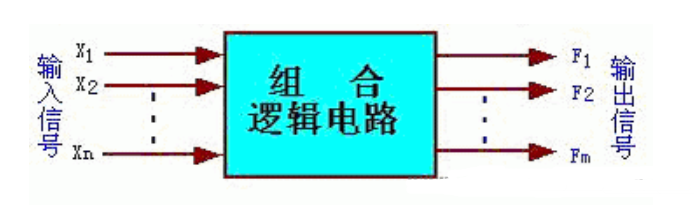
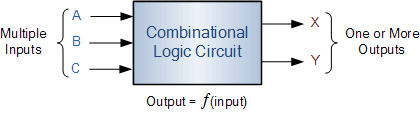
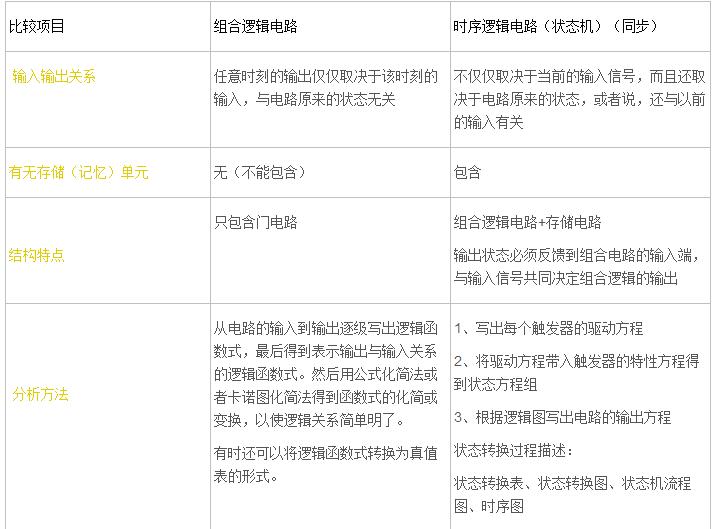
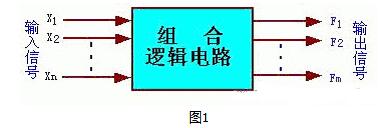
組合邏輯電路：在任何時刻的輸出狀態只取決于這一時刻的輸入狀態，而與電路的原來狀態無關的電路。
生活中組合電路的實例（電子密碼鎖，銀行取款機等）
電路結構：由邏輯門電路組成。
電路特點：沒有記憶單元，沒有從輸出反饋到輸入的回路。

說明：本節討論的是SSI電路的分析和設計方法。
6.2.1組合邏輯電路的分析方法
提問：1.描述組合邏輯電路邏輯功能的方法主要有？
（邏輯表達式、真值表、卡諾圖和邏輯圖等。）
2.各種表示法之間的相互轉換？
組合邏輯電路的分析與設計相當于是各種表示法之間的相互轉換。

一、基本分析方法
分析：給定邏輯電路→邏輯功能。

步驟：
1．給定邏輯電路→輸出邏輯函數式
一般從輸入端向輸出端逐級寫出各個門輸出對其輸入的邏輯表達式，從而寫出整個邏輯電路的輸出對輸入變量的邏輯函數式。必要時，可進行化簡，求出最簡輸出邏輯函數式。
2．列真值表
將輸入變量的狀態以自然二進制數順序的各種取值組合代入輸出邏輯函數式，求出相應的輸出狀態，并填入表中，即得真值表。
3．分析邏輯功能
通常通過分析真值表的特點來說明電路的邏輯功能。

二、分析舉例

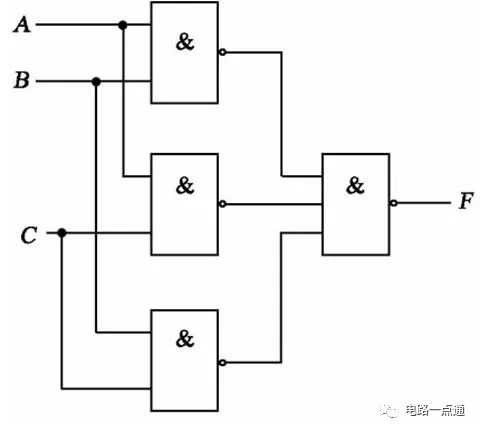
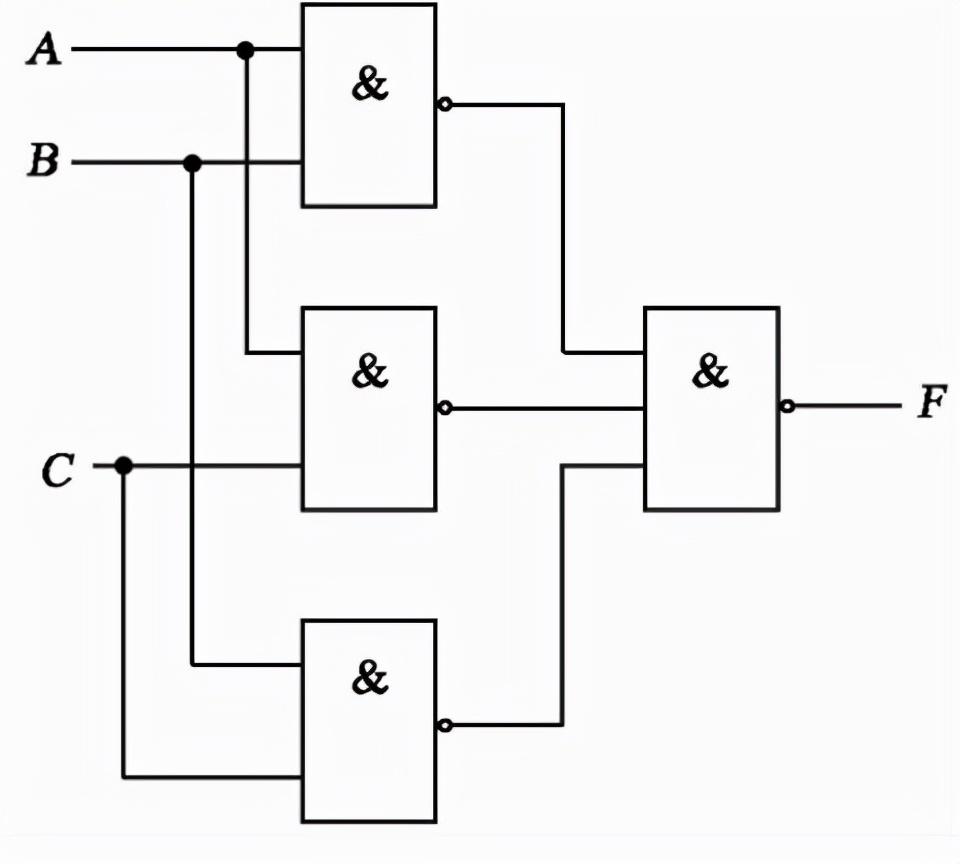
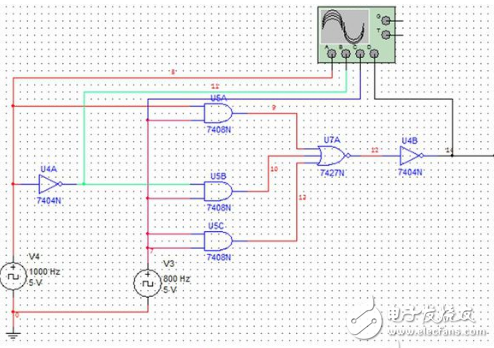
[例6.2.1] 分析圖6.2.1所示邏輯電路的功能。
解：分析步驟
（1）輸出邏輯函數表達式（逐級寫，并且變成便于寫真值表的形式）
?
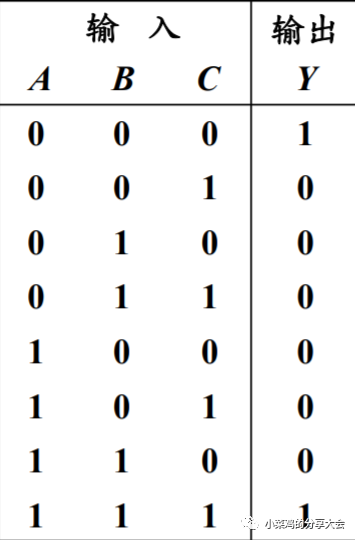
（2）列真值表。將A、B、C各種取值組合代入式中，可列出真值表。
?
（3）邏輯功能分析。
由真值表可看出：在輸入A、B、C三個變量中，有奇數個1時，輸出Y為1，否則Y為0，因此，圖6.2.1所示電路為三位判奇電路，又稱為奇校驗電路。

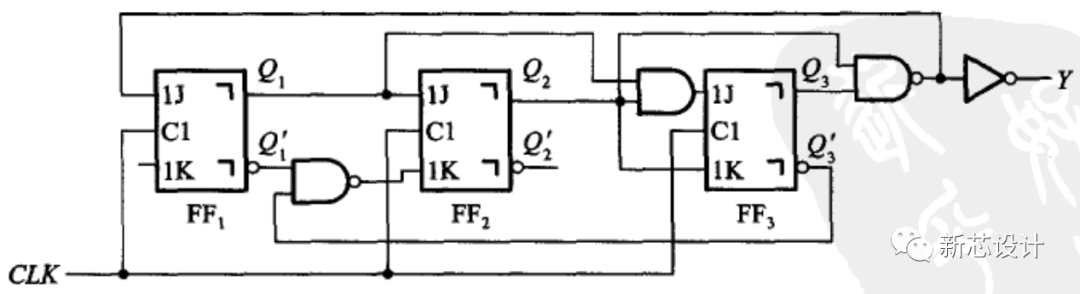
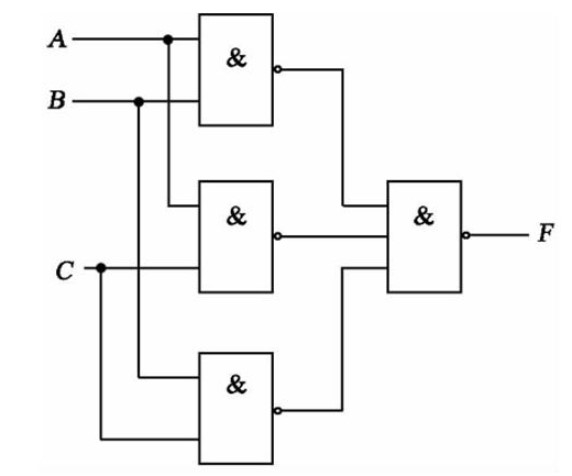
［例6.2.2］分析圖6.2.2所示電路的邏輯功能，并指出該電路設計是否合理。
解：分析步驟
（l）輸出邏輯函數表達式

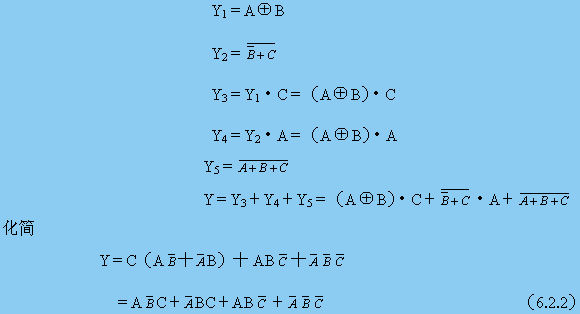
（2）真值表。
?
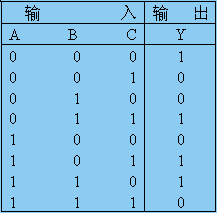
（3）邏輯功能分析。由表6.2.2可看出，圖6.2.2所示電路的A、B、C三個輸入中有偶數個1時，輸出Y為1，否則Y為0。因此，圖6.2.2所示電路為三位判偶電路，又稱偶校驗電路。
（4）改進：這個電路使用門的數量太多，設計并不合理，可用較少的門電路來實現。
變換表達式

可用異或門和同或門實現，電路如圖6.2.3所示。

歸納總結：1 各步驟間不一定每步都要，如：
省略化簡（本已經成為最簡）
由表達式直接概述功能，不一定列真值表。
2 不是每個電路均可用簡煉的文字來描述其功能。 如Y=AB+CD
6.2.2 組合邏輯電路的設計方法
一、基本設計方法
設計：設計要求→邏輯圖。

步驟（與分析相反）:
1．分析設計要求→列真值表
根據題意設輸入變量和輸出函數并邏輯賦值，確定它們相互間的關系，
然后將輸入變量以自然二進制數順序的各種取值組合排列，列出真值表。
2．根據真值表→寫出輸出邏輯函數表達式
3．對輸出邏輯函數進行化簡
代數法或卡諾圖法
4．根據最簡輸出邏輯函數式→畫邏輯圖。
最簡與一或表達式、與非表達式、或非表達式、與或非表達式、其它表達式

二、設計舉例

1．單輸出組合邏輯電路的設計

［例6.2.3］ 設計一個A、B、C三人表決電路。當表決某個提案時，多數人同意，提案通過，同時A具有否決權。用與非門實現。
解：設計步驟
（1）真值表
設A、B、C三個人，表決同意用1表示，不同意時用0表示；
Y為表決結果，提案通過用1表示，通不過用0表示，
同時還應考慮A具有否決權。
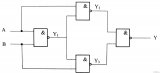
?（3）畫邏輯圖，如圖6.2.5所示

2．多輸出組合邏輯電路的設計

［例6.2.4］ 設計一個將余3碼變換為8421BCD碼的組合邏輯電路。
解：設計步驟
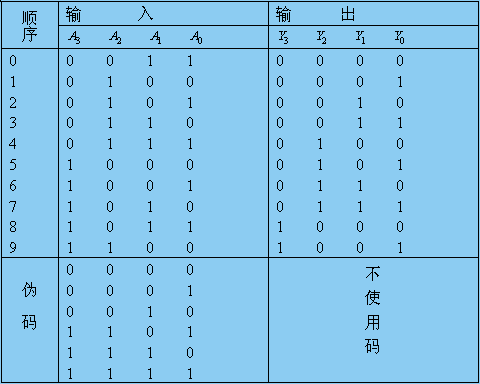
（1）真值表
輸入：余3碼，用A3 、A2 、A1 和A0 表示，
輸出：8421BCD碼，用Y3 、Y2 、Y1 和Y0 表示。
余3碼有六個狀態不用，不會出現，作任意項處理。

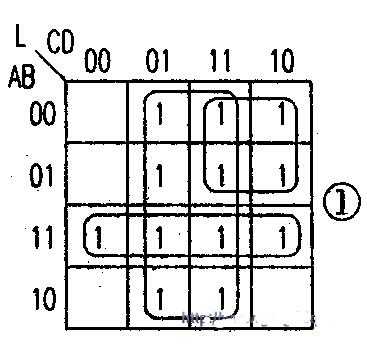
（2）卡諾圖化簡。見教材中圖6.2.6
應畫四張卡諾圖分別求出Y3 、Y2 、Y1 和Y0 的最簡輸出邏輯函數。
含有最小項的方格填1，沒有最小項的方格填0，任意項的方格填×。
由卡諾圖可寫出 Y0、Y1 、Y2 和Y3 的最簡邏輯函數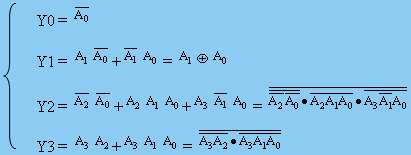

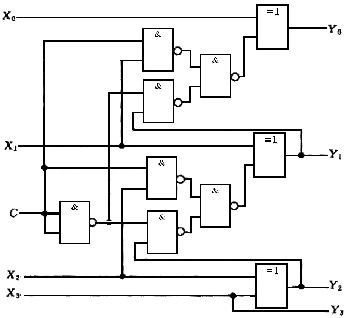
（3）畫邏輯圖。圖6.2.7所示。
將余3碼變換為8421BCD碼的真值表