模擬信號與數字信號

一、模擬信號

　　模擬信號是一種不僅再時間上連續、數值上也連續的物理量，具有無窮多的數值，其數學表達是必較復雜，比如正弦函數、指數函數等。
　　從自然界感知的大部分物理量都是模擬性質的，如速度、壓力、溫度、聲音、重量以及位置等都是最常見的物理量。
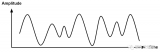
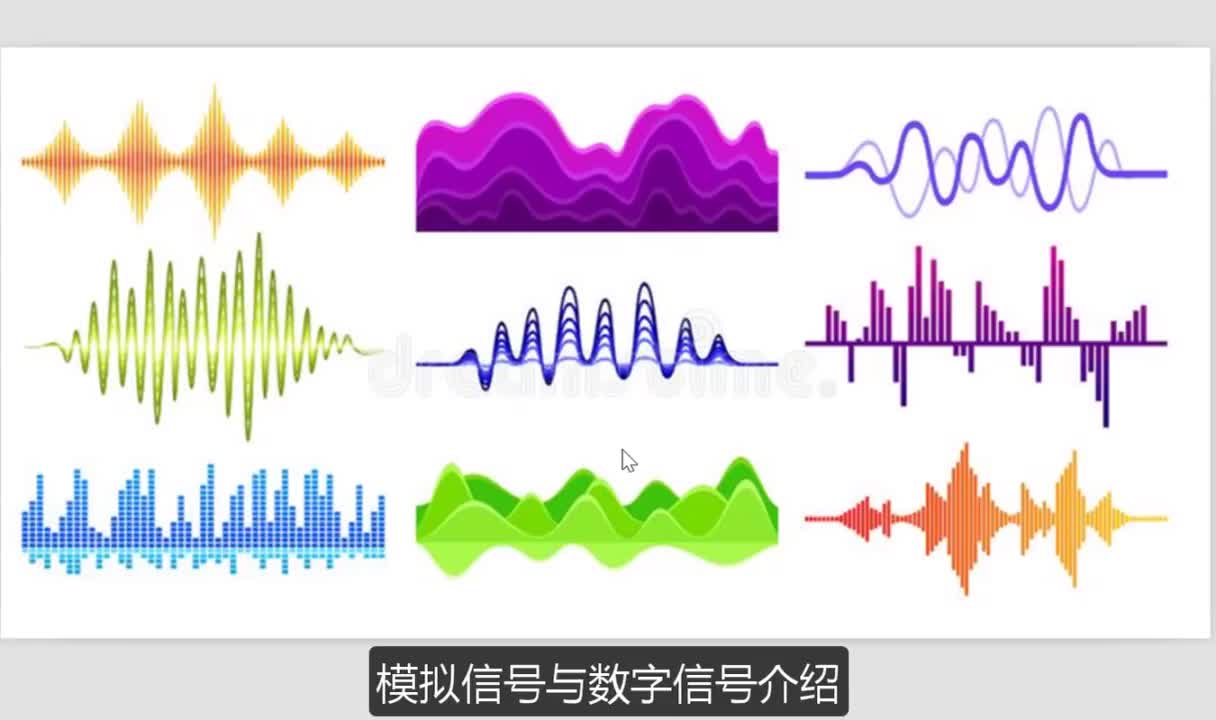
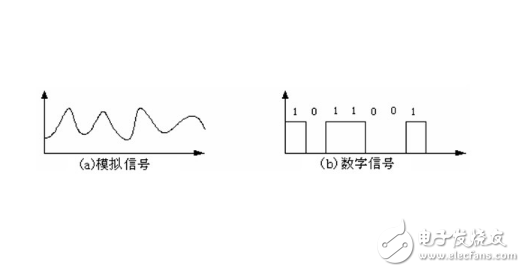
　　圖1.1.1 是幾種常見的模擬信號波形

　　正弦波：例如我們最經常接觸到的聲波。可能你有機會用一臺示波器察看一個真實的聲音波形，你將發現所看到的波形可不像這里所示范的這樣清晰的正弦波，而是看起來非常雜亂的一種波形，確實如此，這只是因為真實的聲音波形中包含了多種頻率的正弦波。另一個例子由發條驅動的鐘擺，將鐘擺的運動軌跡延時間軸展開，得到的連續波形正好就是一個正弦波形。
　　調幅波：自從發明收音機以來，普通百姓就開始與調幅波打交道了，這種波形是以一種頻率很高的正弦波作為載波，在此基礎上疊加一個頻率較低的信號波就形成了入圖所示得波形。
阻尼振蕩波：凡是自然界中可以看到的振蕩運動，都可以觀察到這種波形，比如彈簧的自由振動、鐘擺的自由運動（不同于由發條驅動得鐘擺運動）等，如果說這些還有人工的痕跡，那么水波的漣漪則是在自然不過的了。
　　指數衰減波：許多發光物質都具有這種波形，也就是熒光壽命。我們平時使用的日光燈就是一個例子，當我們將一個點亮的日光燈的電源切斷時，可以觀察到日光燈不是一下子就熄滅，而是有一個短暫的熄滅過程，也就是通常所說的日光燈的余輝。
　　在電子技術中通常采用一些傳感器將這些信號轉換為電流、電壓或電阻等電學量。這些同樣是模擬量，因為如果采用一臺示波器來測量這些電學量的波形的話，將觀察到與圖1.1.2圖示波形一樣的波形。
　　實際使用中電流和電壓常用圖形來表示。
　　下面我們看到的就是一個幅值為0～5V、周期為100ms的電壓波形：

圖1.1.2 周期性電壓波形

　　圖中電壓的幅值按照正弦波形周期性地變化，圖中顯示了兩個完整的波形，起始相位為零，如果想確定其中值的個數是不可能的，其值的個數有無窮多個。
　　正如我們在模擬電路中所學習的，周期性模擬信號的基本參數之一是頻率，也可以用周期表示。通常頻率用f表示，單位為赫茲（Hz）
；周期用T表示，單位為秒（s）。二者之間的關系是互為倒數，即有。圖1.1.2中已知電壓波形的周期Ｔ＝100ms，則頻率為10Hz，該電壓的幅值介于0～5V之間，值的個數為無窮大。
　　典型的模擬信號包括工頻信號、射頻信號、視頻信號等。我國和歐洲的工頻信號的頻率為50Hz ，美國為60Hz 。調幅波的射頻信號在 530Hz～1600kHz之間。調頻波的射頻信號在880MHz～108MHz之間。甚高頻（VHF）和超高頻（UHF）視頻信號在6GHz以上。

二、數字信號

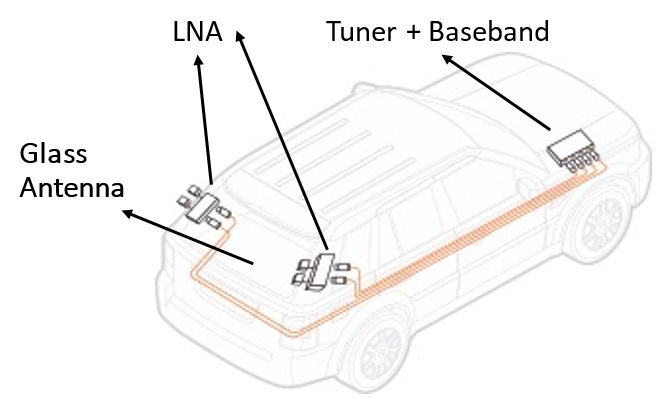
　　電子系統中一般含有模擬和數字兩種構件，通常使用的收音機等
，其中的電路結構主要是模擬電路，比如功率放大器，不過現在有許多音響系統中不僅包含模擬電路，而且已經有了數字模塊，比如CD機
，其中主要的部件就是數字模塊；而像電腦這樣一類的電子系統，則主要就是建立在數字技術上的，但即使是所謂的純數字系統，仍然離不開模擬電路，因為數字電路實事上可以說是模擬電路的一種特例，比如說在模擬電路中我們采用晶體管的線性工作區間，而數字電路則采用晶體管的非線性工作區間，因此說模擬電路是電子系統中必須的組成部分。
　　人們發現在對信號的存儲、分析和傳輸中，數字電路更具優越性
。為了能夠處理存儲連續變化的模擬信號，數字電路采用二進制數首先對其進行量化處理后，再使用復雜的數字系統來實現信號的存儲、分析和量化。

1.二值數字邏輯和邏輯電平

　　二進制數正好是利用二值數字邏輯中的０和１來表示的。二值數字邏輯是Binary Digital Logic的譯稱。
　　與模擬信號相反，數字數字信號在時間上和數值上均是離散的，而離散信號的值只有真或假，是與不是，因此可以使用二進制數中的０和１來表示。需要注意的是這里的０和１并非通常意義上的０和１
，也就是說并不像在十進制中０和１有大小之分，這里的０和１指的是邏輯０和邏輯１。
　　因此我們可以將其稱之為二值數字邏輯或簡稱為數字邏輯。
　　二值數字的產生，是基于客觀世界中存在許多可以用彼此相關又互相對立的兩種狀態來描述的事物，比如人的性別，不是男的就是女的，開關的開與關等，就是這樣一種關系。很顯然，這些都具有明顯的二值特性，因此完全可以用電子器件的開關特性來表示。比如，利用晶體管的非線性特性制作成的開關二極管，工作時僅有兩種狀態，不是導通就是關斷，也是一個二值特性，因此可以用其來表示人的性別等。
　　當開關器件起作用時，電路中只可能出現兩種電壓值，當開關器件導通時，開關后的電路中將有電流流過（比如串聯于三極管發射極的負載），因而將可得到一個較高的電壓值，而當開關器件關斷時，開關后的電路中將沒有電流流過，因而將只能得到一個較低的電壓值
，從而在電路中將形成離散的電壓信號，也叫數字電壓，通常稱之為邏輯電平。
　　應該注意的是邏輯電平不是一個具體的物理量，而是物理量的相對表示。比如，當使用示波器測量一個音響設備的輸出時，你可觀察到一個輸出電壓幅值連續變化的波形，但是將該輸出信號量化成二值信號后，你觀察到的只是一系列電壓值不是５Ｖ就是０Ｖ的離散電壓值，很顯然我們不能因此就說該音響設備的輸出就是５Ｖ。

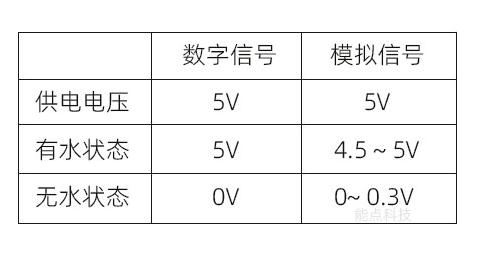
表1.1.1 邏輯電平與電壓值的關系

　　從表中可以看到，+5V的電壓值可以用二值邏輯中的1或0來表示，就看你使用的是正邏輯還是負邏輯。在邏輯電平中則使用高電平來表示。事實上高電平并非就只等于+5V，可以是3V，還可以是其它任何值。
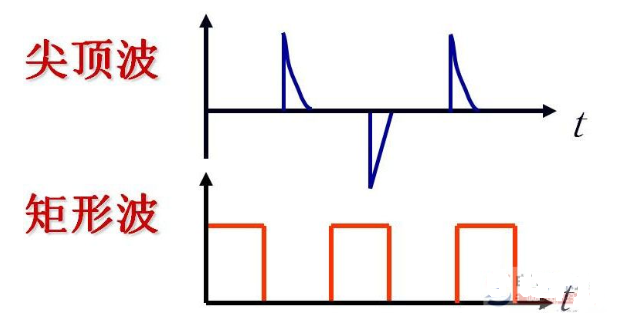
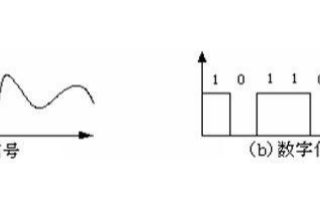
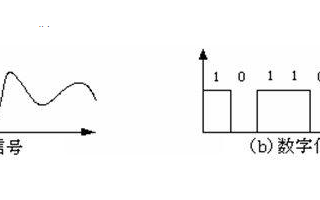
　　圖1.1.3表示用邏輯電平描述的數字波形，其中圖1.1.3a的邏輯0表示0V，邏輯1表示5V；圖1.1.3b的邏輯0表示5V，邏輯1表示0V；圖1.1.3c 則是一個16位長數據的圖形表示。

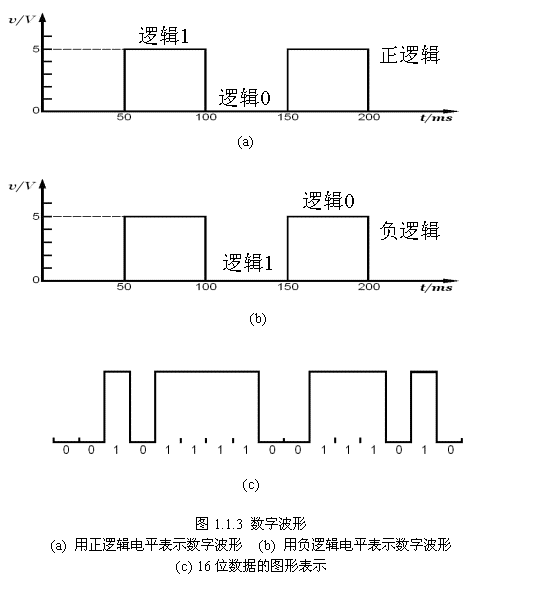
2.數字波形

　　數字波形是邏輯電平對時間的圖形表示。通常，我們將只有兩個離散值的波形稱之為脈沖波形，在這一點上脈沖波形與數字波形是一致的，只不過數字波形用邏輯電平表示，而脈沖波形用電壓值表示而已。
　　與模擬波形的定義相同，數字波形也有周期性和非周期性之分。圖1.1.4表示了這兩類數字波形：

　　周期性數字波形同樣用周期T或頻率f來描述；而脈沖波形的頻率常稱為脈沖重復率PRR--Pulse Repetition Rate。
　　脈沖波形的參數：
　　脈沖寬度：t_w表示，表示脈沖作用的時間；
　　占空比：q，表示脈沖寬度t_w占整個周期T的百分數，常用下式來表示：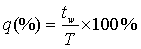
　　占空比是一個重要參數，其定義同樣適用于數字波形。
　　圖1.1.5表示兩種數字波形及其周期、頻率、脈沖寬度和占空比：

　　例題1.1.1設周期性數字波形的高電平持續6ms，低電平持續10ms
，求占空比q？

解：根據給定的高電平持續時間有t_w= 6ms，而高電平與低電平持續時間之和即為周期T

　　所以有 Ｔ＝6ms＋10ms＝16ms

　　

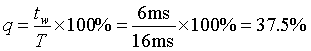
　　到目前為止，我們所討論的數字波形都是理想波形，然而實際的數字系統中，數字波形的升降都要經歷一段時間，也就是說波形存在上升時間t_r和下降時間t_f 。
　　上升時間t_r的定義是：從脈沖幅值的10%到90%所經歷的時間；下降時間t_f的定義剛好相反：從脈沖幅值的90%到10%所經歷的時間。t_r和t_f的典型值約為幾個納秒（ns），視不同類型的器件和電路而異。
　　脈沖寬度的定義是脈沖幅值為50%時前后兩個時間點所跨越的時間。非理想脈沖如圖1.1.6所示：

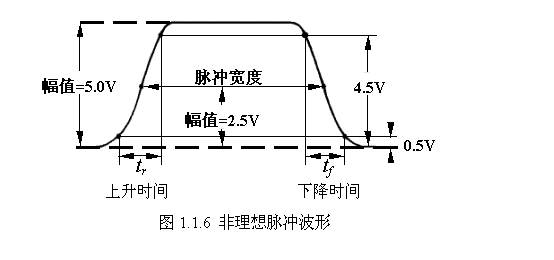
　　例題1.1.2 試繪出一脈沖波形，設它的占空比為50%，脈沖寬度 t_w＝100ns，上升時間t_r＝10ns，下降時間t_f＝20ns。

解：根據題意，可繪出脈沖波形如下：

圖1.1.7 例1.1.2的波形圖

　　一般情況下波形的上升或下降時間均要比高電平或低電平的持續時間要小很多，畫波形的目的主要是為了了解高、低電平所經歷的時間。因此在理想波形中就只有高、低電平，而忽略了上升和下降時間
。本課程中所用的數字波形將采用理想波形。
　　當然，實際中碰到的波形，不管從示波器上來看，其上升沿和下降沿是多么的直，t_r和t_f都不可能為零，只是在數字電路中，只需關注邏輯電平的高低，因此在畫波形時只需畫出高低電平所經歷的時間即可，無需畫出上升沿和下降沿。

(a)

(b)

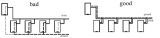
圖1.1.8 用邏輯1和0表示的二值位行圖
(a) 對稱方波 (b) 二值數據

　　上圖為一個二值位形圖，其中１或１占用的最小時間稱為位時間
，也就是１位數據所占用的時間。我們將每秒鐘所傳輸的位數稱為數據率或比特率。
　　例題1.1.3 某通信系統每秒中傳輸1.544兆位數據，求每位數據的時間。

解：根據題意，只需將1.544M倒數，即可求得每位數據的時間為：

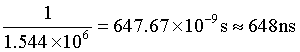
　　舉例來說，象圖1.1.8b中看到的22位的二值位形圖，如果每一位數據所占用的時間是648ns，則22位共占用14256ns，也就是14.256微秒，而其數據率就是1.544兆。
　　在設計數字集成電路時，有時為了分析各種信號之間的邏輯關系
，需要將多個數字波形按時間排列在一起，用來表明相互間的時間關系，我們將這樣一種關系圖稱為時序圖（Timing diagram）。
　　時序圖中的每一個波形都被稱為時間信號。時序圖被廣泛運用在設計數字集成電路中，在設計存儲器、微處理機等數字應用電路時均須附有時序圖，以便數字系統的分析、應用和設計。
　　圖1.1.9就是一個時序圖的例子：

圖1.1.9 數字時序圖

　　圖中CP為時鐘脈沖信號，用作系統中的時間參考信號，一般由石英晶體振蕩器來產生，如圖所示波形為對稱方波。關于圖中各個波形的具體作用，將在以后的課程加以介紹

3.模擬量的數字表示

　　為便于存儲、分析和傳輸，常常需要將模擬信號轉換為數字信號
。
　　在數字電路中用數字0、1的編碼來表示一個模擬量，這里的編碼所指的是數字0、1的字符串，圖1.1.3和圖1.1.8所示的數字波形即是這種編碼的圖形。這樣一種編碼實際上就是二進制編碼。
　　下面通過圖1.1.10的圖示來了解用數字表示模擬信號的過程：

　　取其中Ａ、Ｂ、Ｃ３個取樣點。以Ｂ點為例，該點的模擬電壓為3V，將其送入一個模數轉換器后可得到以數字０、１表示的數字電壓
，如圖1.1.10b所示。同樣地也可以得到Ａ、Ｃ點的數字編碼。
　　當信號的取樣點數足夠多時，原信號就可以被較真實地復制下來
。
　　當然，必要的話還可以通過數模轉換器將已經數字化的信號還原成模擬信號。